Toán 10 tập 1 trang 87 Bài 4: Tổng và hiệu của hai vectơ

Giải toán 10 tập 1 trang 87 Cánh diều bài 4 có đáp án chi tiết cho từng bài tập trong sách giáo khoa toán lớp 10 tập 1 Cánh diều. Mời các em học sinh cùng quý phụ huynh tham khảo.

Toán 10 tập 1 trang 87

Bài 1 trang 87 Toán 10 tập 1 Cánh diều

Cho ba điểm M, N, P. Vecto $\overrightarrow u = \overrightarrow {NP} + \overrightarrow {MN}$ bằng vecto nào sau đây?

A.$ \overrightarrow {PN}$

B. $\overrightarrow {PM}$

C. $\overrightarrow {MP}$

D.$\overrightarrow {NM}$

Lời giải

Vận dụng tính chất giao hoán ta có: $\overrightarrow u = \overrightarrow {NP} + \overrightarrow {MN} = \overrightarrow {MN} + \overrightarrow {NP} = \overrightarrow {MP}$

Chọn C.

Bài 2 trang 87 Toán 10 tập 1 Cánh diều

Cho ba điểm D, E, G. Vecto $\overrightarrow v = \overrightarrow {DE} + ( – \overrightarrow {DG} )$ bằng vecto nào sau đây?

A. $\overrightarrow {EG}$

B. $\overrightarrow {GE}$

C. $\overrightarrow {GD}$

D. $\overrightarrow {ED}$

Lời giải

Ta có: $\overrightarrow {GD} = – \overrightarrow {DG}$

$\Rightarrow \overrightarrow v = \overrightarrow {DE} + ( – \overrightarrow {DG} ) = \overrightarrow {DE} + \overrightarrow {GD}$

$\Rightarrow \overrightarrow v = \overrightarrow {GD} + \overrightarrow {DE} = \overrightarrow {GE}$

(tính chất giao hóan)

Chọn B.

Bài 3 trang 87 Toán 10 tập 1 Cánh diều

Cho bốn điểm A, B, C, D. Chứng minh:

a) $\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB}$

b) $\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow 0$

Lời giải

a)

$\begin{array}{l}\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} \\ \Leftrightarrow \overrightarrow {AB} – \overrightarrow {CB} = \overrightarrow {AD} – \overrightarrow {CD} \\ \Leftrightarrow \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AD} + \overrightarrow {DC} \\ \Leftrightarrow \overrightarrow {AC} = \overrightarrow {AC} \end{array}$ (luôn đúng)

b) $\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow 0$

Ta có:

$\begin{array}{l}\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {BC} + \overrightarrow {DA} = (\overrightarrow {AB} + \overrightarrow {BC} ) + (\overrightarrow {CD} + \overrightarrow {DA} )\\ = \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow 0 \end{array}$

Chú ý khi giải

+) Hiệu hai vecto chung gốc: $\overrightarrow {AB} – \overrightarrow {AC} = \overrightarrow {CB}$ (suy ra từ tổng $\overrightarrow {AB} = \overrightarrow {AC} + \overrightarrow {CB}$)

+) Với 4 điểm A, B, C, D bất kì ta có: $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow {AA} = \overrightarrow 0$

Bài 4 trang 87 Toán 10 tập 1 Cánh diều

Cho hình hình hành ABCD, gọi O là giao điểm của AC và BD. Các khảng định sau đúng hay sai?

a) $|\overrightarrow {AB} + \overrightarrow {AD} |\; = \;|\overrightarrow {AC} |$

b) $\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {CB}$

c) $\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} + \overrightarrow {OD}$

Lời giải

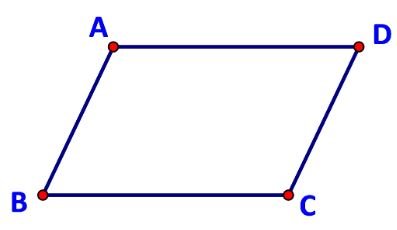
a) Theo quy tắc hình bình hành ta có: $\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC}$

$\Rightarrow |\overrightarrow {AB} + \overrightarrow {AD} |\; = \;|\overrightarrow {AC} |$

Vậy mệnh đề này đúng.

b) Ta có: $\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} = \overrightarrow {BC} \ne \overrightarrow {CB}$

Vậy mệnh đề này sai.

c) Ta có:$ \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} + \overrightarrow {OD} \Leftrightarrow \overrightarrow {OA} – \overrightarrow {OB} = \overrightarrow {OD} – \overrightarrow {OC} \Leftrightarrow \overrightarrow {BA} = \overrightarrow {CD}$

(Đúng vì ABCD là hình bình hành)

Vậy mệnh đề này đúng.

Bài 5 trang 87 Toán 10 tập 1 Cánh diều

Cho đường tròn tâm O. Giả sử A, B là hai điểm nằm trên đường tròn. Tìm điều kiện cần và đủ để hai vecto $\overrightarrow {OA}$ và $\overrightarrow {OB}$ đối nhau.

Lời giải

Hai vecto $\overrightarrow {OA}$ và $\overrightarrow {OB}$ đối nhau $\Leftrightarrow$

hai tia OA, OB đối nhau và OA = OB.

$\Leftrightarrow$ O là trung điểm của AB hay AB là đường kính của đường tròn (O).

Vậy điều kiện cần và đủ để hai vecto $\overrightarrow {OA}$ và $\overrightarrow {OB}$

đối nhau là AB là đường kính của đường tròn (O).

Bài 6 trang 87 Toán 10 tập 1 Cánh diều

Cho ABCD là hình bình hành. Chứng minh $\overrightarrow {MB} – \overrightarrow {MA} = \overrightarrow {MC} – \overrightarrow {MD}$ với mỗi điểm M trong mặt phẳng.

Lời giải

Ta có: $\overrightarrow {AM} = – \overrightarrow {MA} ,\;\overrightarrow {DM} = – \overrightarrow {MD}$

$\Rightarrow \overrightarrow {MB} – \overrightarrow {MA} = \overrightarrow {MB} + \overrightarrow {AM} = \overrightarrow {AM} + \overrightarrow {MB} = \overrightarrow {AB}$

Tương tự ta có: $\overrightarrow {MC} – \overrightarrow {MD} = \overrightarrow {MC} + \overrightarrow {DM} = \overrightarrow {DM} + \overrightarrow {MC} = \overrightarrow {DC}$

Mà $\overrightarrow {AB} = \overrightarrow {DC}$ (do ABCD là hình bình hành)

$\Rightarrow \overrightarrow {MB} – \overrightarrow {MA} = \overrightarrow {MC} – \overrightarrow {MD}$

Bài 7 trang 87 Toán 10 tập 1 Cánh diều

Cho hình vuông ABCD có cạnh a. Tính độ dài các vecto sau:

a) $\overrightarrow {DA} + \overrightarrow {DC}$

b) $\overrightarrow {AB} – \overrightarrow {AD}$

c) $\overrightarrow {OA} + \overrightarrow {OB}$ với O là giao điểm của AC và BD.

Lời giải

a) Do ABCD cũng là một hình bình hành nên $\overrightarrow {DA} + \overrightarrow {DC} = \overrightarrow {DB}$

$\Rightarrow \;|\overrightarrow {DA} + \overrightarrow {DC} |\; = \;|\overrightarrow {DB} |\; = DB = a\sqrt 2$

b) Ta có: $\overrightarrow {AD} + \overrightarrow {DB} = \overrightarrow {AB} \Rightarrow \overrightarrow {AB} – \overrightarrow {AD} = \overrightarrow {DB}$

$\Rightarrow \left| {\overrightarrow {AB} – \overrightarrow {AD} } \right| = \left| {\overrightarrow {DB} } \right| = DB = a\sqrt 2$

c) Ta có: $\overrightarrow {DO} = \overrightarrow {OB}$

$\Rightarrow \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OA} + \overrightarrow {DO} = \overrightarrow {DO} + \overrightarrow {OA} = \overrightarrow {DA}$

$\Rightarrow \left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = \left| {\overrightarrow {DA} } \right| = DA = a$.

Bài 8 trang 87 Toán 10 tập 1 Cánh diều

Cho ba lực $\overrightarrow {{F_1}} = \overrightarrow {OA} ,\;\overrightarrow {{F_2}} = \overrightarrow {OB}$ và $\overrightarrow {{F_3}} = \overrightarrow {OC}$ cùng tác động vào một vật tại điểm O và vật đứng yên. Cho biết cường độ của $\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}}$ đều là 120 N và $\widehat {AOB} = {120^o}$ . Tìm cường độ và hướng của lực $\overrightarrow {{F_3}}$ .

Lời giải

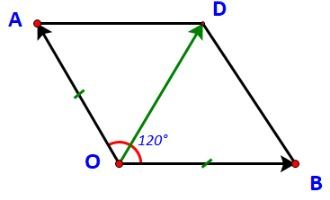
Gọi D là đỉnh thứ tư của hình bình hành OADB.

Khi đó ta có: $\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} = \overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OD}$

Ta có: OA = OB = 120 suy ra tứ giác OADB là hình thoi

$\Rightarrow \widehat {AOD} = \widehat {BOD} = \frac{{{{120}^o}}}{2} = {60^o}$

$\Rightarrow \Delta$ AOD đều (do OA = AD và $\widehat {AOD} = {60^o}$ )

$\Rightarrow$ OD = OA = 120

Mặt khác: Do vật đứng yên nên $\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} + \;\overrightarrow {{F_3}} = \overrightarrow 0 \Leftrightarrow \;\overrightarrow {{F_3}} = – (\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} ) = – \overrightarrow {OD}$

Suy ra $\overrightarrow {OC}$ là vecto đối của $\overrightarrow {OD}$

Ta có: $\widehat {COA} = {180^o} – \widehat {AOD} = {120^o}$

.Tương tự: $\widehat {COB} = {120^o}$

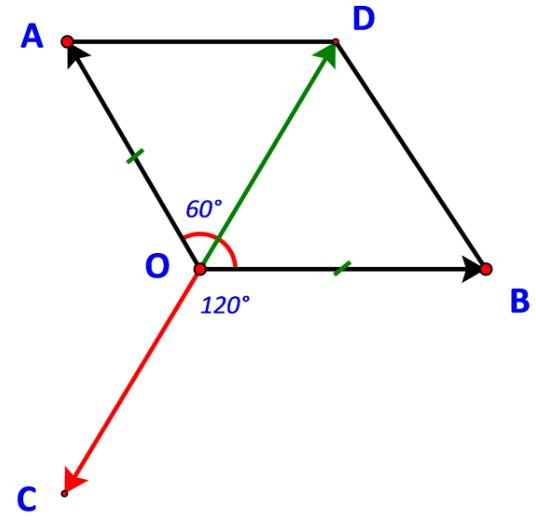
Vậy cường độ của lực $\overrightarrow {{F_3}}$ là 120 N, tạo với lực $\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}}$ góc ${120^o}$.

Bài 9 trang 87 Toán 10 tập 1 Cánh diều

Một dòng sông chảy từ phía bắc xuống phía nam với vận tốc là 10 km/h. Một chiếc ca nô chuyển động từ phía đông sang phía tây với vận tốc 40 km/h so với mặt nước. Tìm vận tốc của ca nô so với bờ sông.

Lời giải

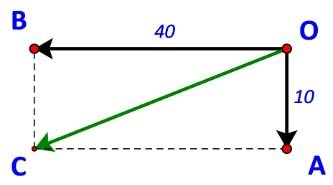
Gọi O là vị trí của ca nô.

Vẽ $\overrightarrow {OA}$

là vận tốc dòng nước (chảy từ phía bắc xuống phía nam), $\overrightarrow {OB}$

là vận tốc riêng của ca nô (chuyển động từ phía đông sang phía tây)

Khi đó vecto vận tốc của ca nô so với bờ sông là vecto $\overrightarrow {OA} + \overrightarrow {OB}$

Gọi C là đỉnh thứ tư của hình bình hành OACB, ta có: $\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB}$

Xét tam giác OBC vuông tại B ta có: BC = 40; BC = OA = 10.

$\Rightarrow OC = \sqrt {O{B^2} + B{C^2}} = 10\sqrt {17}$

Vậy vận tốc của ca nô so với bờ sông là $10\sqrt {17}$ km/h.