Toán 7 tập 1 trang 54 Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song

Giải toán 7 tập 1 trang 54 bài 10 sách Kết nối tri thức có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 7 Kết nối tri thức mới. Mời các em học sinh cùng quý phụ huynh tham khảo.

Trang 51 Toán 7 tập 1

Mở đầu trang 51 Toán 7 Tập 1 Kết nối tri thức

Qua điểm M nằm ngoài đường thẳng a, chúng ta đã biết cách vẽ một đường thẳng b đi qua điểm M và song song với a. Vậy có thể vẽ được bao nhiêu đường thẳng b như vậy?

Lời giải:

Ta có thể vẽ được duy nhất một đường thẳng b như vậy.

1. Tiên đề Euclid về đường thẳng song song

Hoạt động 1 trang 51 Toán 7 Tập 1:

Cho trước đường thẳng a và một điểm M không nằm trên đường thẳng a (H.3.31).

• Dùng bút chì vẽ đường thẳng b đi qua M và song song với đường thẳng a.
• Dùng bút màu vẽ đường thẳng c đi qua M và song song với đường thẳng a.

Em có nhận xét gì về vị trí của hai đường thẳng b và c?

Hướng dẫn giải

Dùng bút chì vẽ đường thẳng b đi qua M và song song với đường thẳng a, ta được:

Dùng bút màu vẽ đường thẳng c đi qua M và song song với đường thẳng a, ta được:

Nhận xét: Hai đường thẳng b và c trùng nhau.

Trang 52 toán 7 tập 1

Luyện tập 1 trang 52 Toán 7 Tập 1:

Phát biểu nào sau đây diễn đạt đúng nội dung của Tiên đề Euclid?

(1) Cho điểm M nằm ngoài đường thẳng a. Đường thẳng đi qua M và song song với a là duy nhất.

(2) Có duy nhất một đường thẳng song song với một đường thẳng cho trước.

(3) Qua một điểm M nằm ngoài đường thẳng a có ít nhất một đường thẳng song song với a.

Hướng dẫn giải

Đáp án chính xác nhất:

1. Cho điểm M nằm ngoài đường thẳng a. Đường thẳng đi qua M và song song với a là duy nhất.

2. Tính chất của hai đường thẳng song song

Hoạt động 2 trang 52 Toán 7 Tập 1:

Vẽ hai đường thẳng song song a,b. Kẻ đường thẳng c cắt đường thẳng a tại A và cắt đường thẳng b tại B. Trên Hình 3.34:

a) Em hãy đo một cặp góc so le trong rồi rút ra nhận xét.

b) Em hãy đo một cặp góc đồng vị rồi rút ra nhận xét.

Hướng dẫn giải

a) Ta có: $\widehat {{B_2}}$ và $\widehat {{A_1}}$ là hai góc ở vị trí so le trong. Đo góc ta được: $\widehat {{B_2}}= \widehat {{A_1}}$

b) Ta có: $\widehat {{B_1}}$ và $\widehat {{A_1}}$ là hai góc ở vị trí đồng vị. Đo góc ta được: $\widehat {{B_1}}= \widehat {{A_1}}$

Trang 53 Toán 7 tập 1

Luyện tập 2 trang 53 Toán 7 tập 1

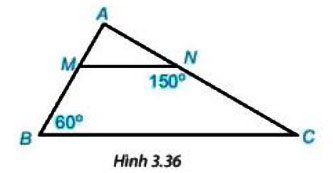
1) Cho hình 3.36. biết MN // BC, $\widehat {ABC} = {60^0};\widehat {MNC} = {150^0}$

. Hãy tính số đo các góc BMN và ACB.

2) Cho hình 3.37, biết rằng xx’ // yy’ và zz’ ⊥ xx’. Tính số đo góc ABy và cho biết zz’ có vuông góc với yy’ không.

Hướng dẫn giải

1) Ta có: MN // BC

=> (Hai góc nằm ở vị trí đồng vị)

Ta lại có: Góc AMN và góc NMB là hai góc kề bù.

=> $\widehat {AMN} + \widehat {NMB} = {180^0}$

=> $\widehat {NMB} = {180^0} – \widehat {AMN} = {180^0} – {60^0} = {120^0}$

Vậy $\widehat {NMB} = {120^0}$

Ta có: Góc ANM và góc MNC là hai góc kề bù.

=> $\widehat {ANM} + \widehat {MNC} = {180^0}$

=> $\widehat {ANM} = {180^0} – \widehat {MNC} = {180^0} – {150^0} = {30^0}$

Mà NM // BC

=> $\widehat {ANM} = \widehat {ACB} = {30^0}$ (Hai góc ở vị trí đồng vị)

Vậy $\widehat {ACB} = {30^0}$

2) Ta có: zz’ ⊥ xx’ => $\widehat {zAx’}$ =90⁰

Mà xx’ // yy’

=> $\widehat {zAx‘}=\widehat {ABy‘}$=90⁰(hai góc ở vị trí đồng vị)

=> zz’ ⊥ yy’

Bài 3.17 trang 53 Toán 7 tập 1

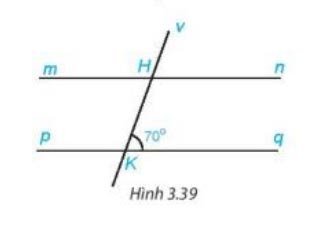
Cho hình 3.39, biết rằng mn // pq. Tính số đo góc mHK, vHn.

Hướng dẫn giải:

Theo bài ra ta có: mn // pq

=> $\widehat {mHK} = \widehat {HKq} = {70^0}$ (hai góc ở vị trí so le trong)

Vậy $\widehat {mHK} = {70^0}$

Ta lại có mn // pq

=> $\widehat {vHn}$ = $\widehat {HKq}$ = ${70^0}$ (hai góc ở vị trí đồng vị)

Vậy $\widehat {vHn}$ = ${70^0}$

Bài 3.18 trang 53 Toán 7 tập 1

Cho hình 3.40:

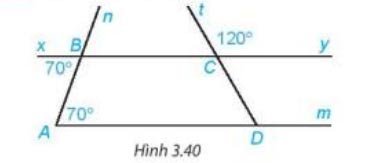
a) Giải thích tại sao Am // By.

b) Tính số đo góc CDm.

Hướng dẫn giải:

a) Quan sát hình vẽ:

Ta có: $\widehat {xBA} = \widehat {BAD} = {70^0}$

Mà hai góc nằm ở vị trí so le trong.

=> Am // By (dấu hiệu hai đường thẳng song song)

b) Ta có: Am // By (Chứng minh câu a)

=> $\widehat {tCy} = \widehat {CDm} = {120^0}$ (hai góc ở vị trí đồng vị)

Vậy $\widehat {CDm} = {120^0}$

Trang 54 toán 7 tập 1

Bài 3.19 trang 54 Toán 7 tập 1

Cho hình 3.41:

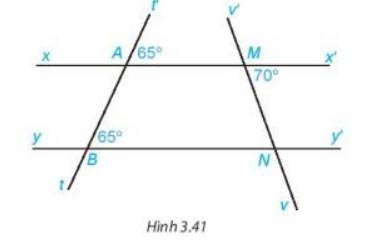
a) Giải thích tại sao xx’ // yy’.

b) Tính số đo góc MNB.

Hướng dẫn giải:

a) Quan sát hình vẽ:

Ta có: $\widehat {t’Ax’}= \widehat{ABy’}=65^0$

Mà hai góc nằm ở vị trí đồng vị.

=> xx’ // yy’ (dấu hiệu hai đường thẳng song song)

b) Ta có: xx’ // yy’ (Chứng minh câu a)

=> $\widehat {x’MN}=\widehat {MNB}$=70⁰ (hai góc ở vị trí so le trong)

Vậy $\widehat {MNB} = {70^0}$

Bài 3.20 trang 54 Toán 7 tập 1

Cho hình 3.42, biết rằng Ax // Dy, $\widehat A = {90^0};\widehat {BCy} = {50^0}$ . Tính số đo các góc ADC và ABC.

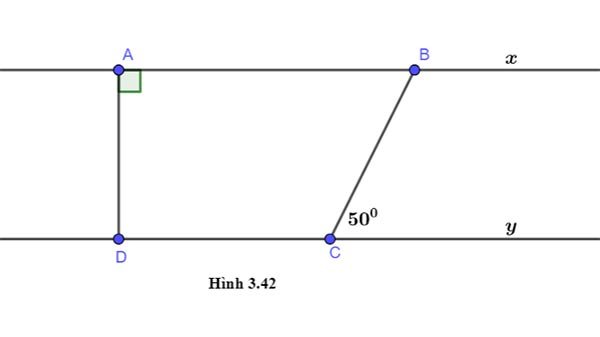
Hướng dẫn giải:

Theo bài ra ta có: Ax // By

Ta lại có: $\widehat A = {90^0}$

=> $\widehat A = \widehat {ADC} = {90^0}$ (Hai góc ở vị trí đồng vị)

Ta có: Ax // By

=> $\widehat {ABC} = \widehat {BCy} = {50^0}$ (Hai góc ở vị trí so le trong)

Vậy $\widehat {ADC} = {90^0};\widehat {ABC} = {50^0}$

Bài 3.21 trang 54 Toán 7 tập 1

Cho hình 3.43. Giải thích tại sao:

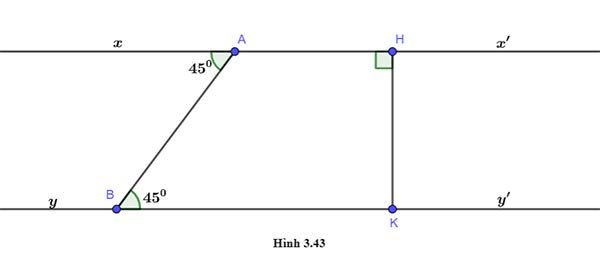
a) Ax’ // By

b) By ⊥ HK

Hướng dẫn giải:

Quan sát hình vẽ

a) Ta có: $\widehat {xAB} = \widehat {ABK} = {45^0}$ Mà hai góc nằm ở vị trí so le trong )

=> Ax’ // By (Dấu hiệu nhận biết hai đường thẳng song song)

b) Ta có: Ax’ // By (chứng minh câu a)

Ta lại có: $\widehat {AHK} = {90^0}$

$\Rightarrow \widehat {AHK} = \widehat {HKB} = {90^0}$ (Hai góc đồng vị bằng nhau)

=> By ⊥ HK

Bài 3.22 trang 54 Toán 7 tập 1

Cho tam giác ABC. Vẽ đường thẳng a đi qua A và song song với BC. Vẽ đường thẳng b đi qua B và song song với AC. Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao?

Hướng dẫn giải:

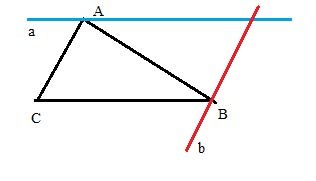
Theo Tiên đề Euclid:

+) Qua điểm A nằm ngoài đường thẳng BC, chỉ có một đường thẳng song song với đường thẳng BC. Đường thẳng đó là a

+) Qua điểm B nằm ngoài đường thẳng AC, chỉ có một đường thẳng song song với đường thẳng BC. Đường thẳng đó là b

Như vậy, có thể vẽ được 1 đường thẳng a, 1 đường thẳng b.

Bài 3.23 trang 54 Toán 7 tập 1

Cho hình 3.44:

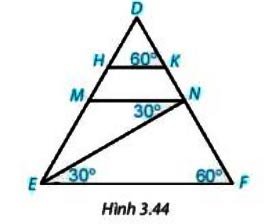
Giải thích tại sao:

a) MN // EF;

b) HK // EF;

c) HK // MN.

Hướng dẫn giải:

Quan sát hình vẽ ta có:

a) Ta có:

$\widehat {MNE} = \widehat {NEF} = {30^0}$ Mặt khác hai góc ở vị trí so le trong

=> MN // EF (Dấu hiệu nhận biết hai đường thẳng song song)

b) Ta có: $\widehat {DKH} = \widehat {DFE} = {60^0}$

Mặt khác hai góc ở vị trí đồng vị

=> HK // EF (Dấu hiệu nhận biết hai đường thẳng song song)

c) Ta có: MN // EF (chứng minh câu a)

HK // EF (chứng minh câu b)

=> HK // MN (tính chất bắc cầu)