Toán 7 tập 1 trang 107 Cánh diều bài 4: Định lý
Toán 7 tập 1 trang 105 Cánh diều bài 4: Định lý
Giải toán 7 tập 1 trang 107 Cánh diều bài 4 có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 7 Cánh diều. Mời các em học sinh cùng quý phụ huynh tham khảo.
Toán 7 tập 1 trang 105 Cánh diều
Khởi động trang 105 Toán 7 tập 1
Bạn Ánh vẽ hai đường thẳng a, b cùng vuông góc với đường thẳng c (Hình 48) và khẳng định với bạn Ngân rằng: “Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng khác thì hai đường thẳng đó song song với nhau”.
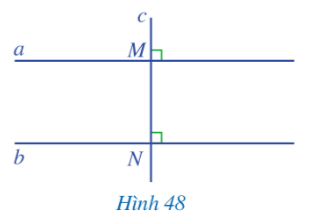
Câu khẳng định có dạng “Nếu … thì …” trong toán học được gọi là gì?
Lời giải:
Câu hỏi này sẽ được giải đáp khi chúng ta học xong bài học hôm nay.
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Câu khẳng định có dạng “Nếu … thì …” trong toán học được gọi là một định lí.
Hoạt động 2 trang 105 Toán 7 tập 1
Xét khẳng định “Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng khác thì hai đường thẳng đó song song với nhau”, ta thấy: Khẳng định này được phát biểu ở dạng “Nếu … thì …”. Trong khẳng định đó, hãy nêu:
– Phần nằm giữa hai từ “Nếu” và từ “thì”;
– Phần nằm sau từ “thì”.
Lời giải:
– Phần nằm giữa hai từ “Nếu” và từ “thì” là “hai đường thẳng phân biệt cùng vuông góc với một đường thẳng khác”;
– Phần nằm sau từ “thì” là “hai đường thẳng đó song song với nhau”.
Toán 7 tập 1 trang 106 Cánh diều
Luyện tập 1 trang 106 Toán 7 tập 1
Viết giả thiết và kết luận của định lí: “Nếu một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng a, b song song với nhau”.
Lời giải::
Giả thiết và kết luận của bài toán được viết như sau:
– Giả thiết: Một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc so le trong bằng nhau.
– Kết luận: Hai đường thẳng a, b song song với nhau.
Toán 7 tập 1 trang 107 Cánh diều
Luyện tập 2 trang 107 Toán 7 tập 1
Chứng minh định lí: Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì các cặp góc so le trong bằng nhau.
Lời giải:
Giả sử đường thẳng c cắt hai đường thẳng phân biệt a, b lần lượt tại hai điểm A và B.
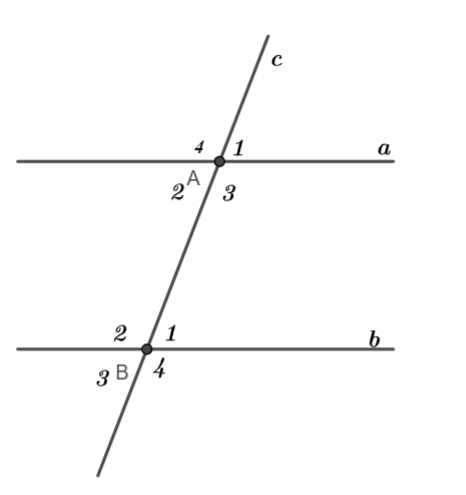
Ta viết giả thiết và kết luận như sau:
| GT | a cắt c tại A, b cắt c tại B $\widehat {{A_1}} = \widehat {{B_1}}$ |
| KL | $\widehat {{A_2}} = \widehat {{B_1}};\widehat {{A_3}} = \widehat {{B_2}}$ |
Chứn minh định lí
Ta có:
$\widehat {{A_1}} = \widehat {{A_2}}$ (Hai góc đối đỉnh)
$\widehat {{A_1}} = \widehat {{B_1}}$ (giả thiết)
=>$\widehat {{A_2}} = \widehat {{B_1}}\left( { = \widehat {{A_1}}} \right)$
Tương tự, ta chứng minh được các cặp góc so le trong còn lại bằng nhau.
Từ đó ta có điều phải chứng minh.
Bài 1 trang 107 Toán 7 tập 1
Vẽ hình minh họa và viết giả thiết, kết luận cho mỗi định lí sau:
a) Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.
b) Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng khác thì chúng song song với nhau.
c) Nếu hai đường thẳng cùng đi qua một điểm và cùng vuông góc với một đường thẳng khác thì hai đường thẳng đó trùng nhau.
Lời giải:
a) Định lí “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại”.
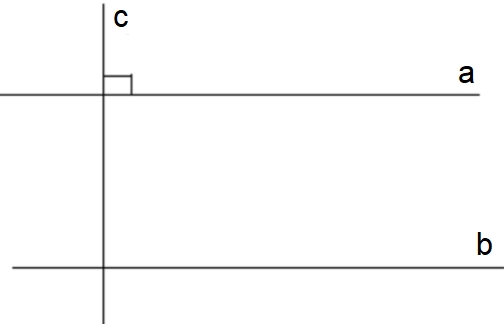
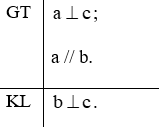
b) Định lí “Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng khác thì chúng song song với nhau”.

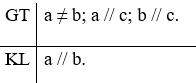
c) Định lí “Nếu hai đường thẳng cùng đi qua một điểm và cùng vuông góc với một đường thẳng khác thì hai đường thẳng đó trùng nhau”.
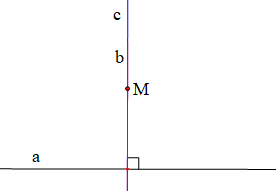

Bài 2 trang 107 Toán 7 tập 1
Cho định lí: “ Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng khác thì chúng song song với nhau.”
a) Vẽ hình minh họa nội dung định lí trên.
b) Viết giải thiết, kết luận của định lí trên.
c) Chứng minh định lí trên.
Lời giải:
Định lí “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng khác thì song song với nhau”.
a) Ta có hình vẽ:
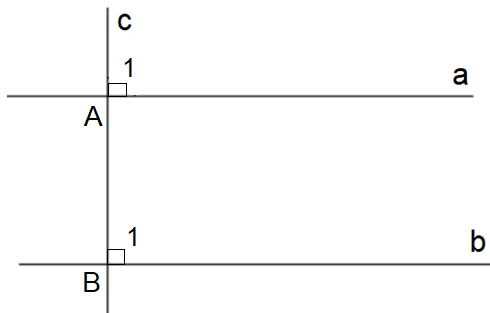
b) Giả thiết, kết luận của định lí:
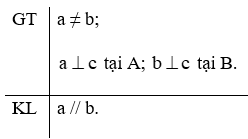
c) Giả sử có 2 đường thẳng phân biệt a,b cùng vuông góc với một đường thẳng c.
Ta có:$\widehat {{A_1}} = \widehat {{B_2}},$ mà hai góc này ở vị trí đồng vị nên a//b (Dấu hiệu nhận biết 2 đường thẳng song song)
Như vậy, định lí trên có thể được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song.
