Toán 7 tập 2 trang 59 Bài 3: Phép cộng, phép trừ đa thức một biến
Toán 7 tập 2 trang 59 Bài 3: Phép cộng, phép trừ đa thức một biến
Giải toán 7 tập 2 trang 59 bài 3 sách Cánh diều có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 7 Cánh diều. Mời các em học sinh cùng quý phụ huynh tham khảo.
Toán 7 tập 2 trang 54
Hoạt động 1 trang 54 Toán 7 tập 2 Cánh diều
a) Thực hiện phép cộng trong mỗi trường hợp sau: 5x2 + 7x2; axk + bxk (k ∈ N* ).
b) Nêu quy tắc cộng hai đơn thức có cùng số mũ của biến.
Hướng dẫn giải:
a) Ta có:
5x2 + 7x2 = (5 + 7)x2 = 12x2.
axk + bxk = (a + b)xk (k ∈ N* ).
b) Quy tắc cộng hai đơn thức có cùng số mũ của biến:
Để cộng hai đơn thức có cùng số mũ của biến, ta cộng hai hệ số với nhau và giữ nguyên phần biến.
Hoạt động 2 trang 54 Toán 7 tập 2 Cánh diều
Cho hai đa thức: P(x) = 5x2 + 4 + 2x và Q(x) = 8x + x2 + 1.
a) Sắp xếp các đa thức P(x), Q(x) theo số mũ giảm dần của biến.
b) Tìm đơn thức thích hợp trong dạng thu gọn của P(x) và Q(x) cho
ở bảng sau rồi cộng hai đơn thức theo từng cột và thể hiện kết quả ở dòng cuối cùng của mỗi cột:
c) Dựa vào kết quả cộng hai đơn thức theo từng cột, xác định đa thức R(x).
Hướng dẫn giải:
a) P(x) = 5x2 + 4 + 2x = 5x2 + 2x + 4.
Q(x) = 8x + x2 + 1 = x2 + 8x + 1.
b)
| Đa thức | Đơn thức có số mũ 2 của biến (Đơn thức chứa x2) | Đơn thức có số mũ 1 của biến (Đơn thức chứa x) | Số hạng tự do (Đơn thức không chứa x) |
| P(x) | 5x2 | 2x | 4 |
| Q(x) | x2 | 8x | 1 |
| R(x) | 6x2 | 10x | 5 |
c) Đa thức R(x) = 6x2 + 10x + 5.
Toán 7 tập 2 trang 55
Luyện tập 1 trang 55 Toán 7 tập 2 Cánh diều
Để cộng hai đa thức P(x), Q(x), bạn Dũng viết như dưới đây có đúng không? Vì sao? Nếu chưa đúng, em hãy sửa lại cho đúng.
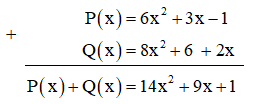
Hướng dẫn giải:
Bạn Dũng viết như trên là không đúng do hai đơn thức có cùng số mũ của biến chưa ở cùng cột.
Sửa lại như sau:
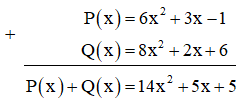
Toán 7 tập 2 trang 56
Hoạt động 3 trang 56 Toán 7 tập 2 Cánh diều
Cho hai đa thức: P(x) = -2x2 + 1 + 3x và Q(x) = -5x + 3x2 + 4.
a) Sắp xếp các đa thức P(x) và Q(x) theo số mũ giảm dần của biến.
b) Viết tổng P(x) + Q(x) theo hàng ngang.
c) Nhóm các đơn thức có cùng số mũ của biến với nhau.
d) Tính tổng P(x) + Q(x) bằng cách thực hiện phép tính trong từng nhóm.
Hướng dẫn giải:
a) P(x) = -2x2 + 1 + 3x = -2x2 + 3x + 1.
Q(x) = -5x + 3x2 + 4 = 3x2+ (-5x) + 4 = 3x2 – 5x + 4.
b) P(x) + Q(x) = (-2x2 + 3x + 1) + (3x2 – 5x + 4)
= -2x2 + 3x + 1 + 3x2 – 5x + 4.
c) P(x) + Q(x) = (-2x2 + 3x2) + (3x – 5x) + (1 + 4).
d) P(x) + Q(x) = (-2x2 + 3x2) + (3x – 5x) + (1 + 4)
= x2 – 2x + 5.
Toán 7 tập 2 trang 57
Hoạt động 4 trang 57 Toán 7 tập 2 Cánh diều
a) Thực hiện phép trừ trong mỗi trường hợp sau: 2x2 – 6x2; axk – bxk (k ∈ N* ).
b) Nêu quy tắc trừ hai đơn thức có cùng số mũ của biến.
Hướng dẫn giải:
a) Ta có:
2x2 – 6x2 = (2 – 6)x2 = -4x2.
axk – bxk = (a – b)xk (k ∈ N* ).
b) Quy tắc trừ hai đơn thức có cùng số mũ của biến:
Để trừ hai đơn thức có cùng số mũ của biến, ta trừ hai hệ số với nhau và giữ nguyên phần biến.
Hoạt động 5 trang 57 Toán 7 tập 2 Cánh diều
Cho hai đa thức: P(x) = 4x2 + 1 + 3x và Q(x) = 5x + 2x2 + 3.
a) Sắp xếp các đa thức P(x), Q(x) theo số mũ giảm dần của biến.
b) Tìm đơn thức thích hợp trong dạng thu gọn của đa thức P(x) và Q(x) cho ở bảng sau rồi trừ hai đơn thức theo từng cột và thể hiện kết quả ở dòng cuối cùng của mỗi cột:
c) Dựa vào kết quả trừ hai đơn thức theo từng cột, xác định đa thức S(x).
Hướng dẫn giải:
a) Ta có:
P(x) = 4x2 + 1 + 3x = 4x2 + 3x + 1.
Q(x) = 5x + 2x2 + 3 = 2x2 + 5x + 3.
b)
| Đa thức | Đơn thức có số mũ 2 của biến (Đơn thức chứa x2) | Đơn thức có số mũ 1 của biến (Đơn thức chứa x) | Số hạng tự do (Đơn thức không chứa x) |
| P(x) | 4x2 | 3x | 1 |
| Q(x) | 2x2 | 5x | 3 |
| S(x) | 2x2 | -2x | -2 |
c) Đa thức S(x) = 2x2 – 2x – 2.
Toán 7 tập 2 trang 59
Bài 1 trang 59 Toán 7 tập 2 Cánh diều
Cho hai đa thức:$R(x) = – 8{x^4} + 6{x^3} + 2{x^2} – 5x + 1 và S(x) = {x^4} – 8{x^3} + 2x + 3.$
Tính:
a) R(x) + S(x);
b) R(x) – S(x).
Hướng dẫn giải:
$a) \begin{array}{l}R(x) + S(x) = – 8{x^4} + 6{x^3} + 2{x^2} – 5x + 1 + {x^4} – 8{x^3} + 2x + 3\\ = ( – 8 + 1){x^4} + (6 – 8){x^3} + 2{x^2} + ( – 5 + 2)x + (1 + 3)\\ = – 7{x^4} – 2{x^3} + 2x – 3x + 4\end{array}$
$b) \begin{array}{l}R(x) – S(x) = – 8{x^4} + 6{x^3} + 2{x^2} – 5x + 1 – ({x^4} – 8{x^3} + 2x + 3)\\ = – 8{x^4} + 6{x^3} + 2{x^2} – 5x + 1 – {x^4} + 8{x^3} – 2x – 3\\ = ( – 8 – 1){x^4} + (6 + 8){x^3} + 2{x^2} + ( – 5 – 2)x + (1 – 3)\\ = – 9{x^4} + 14{x^3} + 2x – 7x – 2\end{array}$
Bài 2 trang 59 Toán 7 tập 2 Cánh diều
Xác định bậc của hai đa thức là tổng, hiệu của:
$A(x) = – 8{x^5} + 6{x^4} + 2{x^2} – 5x + 1$ và$B(x) = 8{x^5} + 8{x^3} + 2x – 3.$
Hướng dẫn giải:
Tổng 2 đa thức:
$\begin{array}{l}A(x) + B(x) = – 8{x^5} + 6{x^4} + 2{x^2} – 5x + 1 + 8{x^5} + 8{x^3} + 2x – 3\\ = ( – 8 + 8){x^5} + 6{x^4} + 8{x^3} + 2{x^2} + ( – 5 + 2)x + (1 – 3)\\ = 6{x^4} + 8{x^3} + 2{x^2} – 3x – 2\end{array}$
Vậy bậc của hai đa thức là tổng là: 4.
Hiệu 2 đa thức:
$\begin{array}{l}A(x) – B(x) = – 8{x^5} + 6{x^4} + 2{x^2} – 5x + 1 – (8{x^5} + 8{x^3} + 2x – 3)\\ = – 8{x^5} + 6{x^4} + 2{x^2} – 5x + 1 – 8{x^5} – 8{x^3} – 2x + 3\\ = ( – 8 – 8){x^5} + 6{x^4} – 8{x^3} + 2{x^2} + ( – 5 – 2)x + (1 + 3)\\ = – 16{x^5} + 6{x^4} – 8{x^3} + 2{x^2} – 7x + 4\end{array}$
Vậy bậc của hai đa thức là hiệu là: 5
Bài 3 trang 59 Toán 7 tập 2 Cánh diều
Bác Ngọc gửi ngân hàng thứ nhất 90 triệu đồng với kì hạn 1 năm, lãi suất x%/năm. Bác Ngọc gửi ngân hàng thứ hai 80 triệu đồng với kì hạn 1 năm, lãi suất (x + 1,5)%/năm. Hết kì hạn 1 năm, bác Ngọc có được cả gốc lẫn lãi là bao nhiêu:
a) Ở ngân hàng thứ hai?
B) Ở cả hai ngân hàng?
Hướng dẫn giải:
a) Số tiền lãi bác Ngọc có được sau kì hạn 1 năm ở ngân hàng thứ hai là:
$\dfrac{{80.(x + 1,5)}}{{100}} = 0,8.(x + 1,5) = 0,8x + 1,2$ (triệu đồng)
Vậy sau kì hạn 1 năm, số tiền bác Ngọc có được cả gốc lẫn lãi ở ngân hàng thứ hai là:
80 + (0,8x + 1,2) = 0,8x + 81,2 (triệu đồng)
b) Số tiền lãi bác Ngọc có được sau kì hạn 1 năm ở ngân hàng thứ nhất là:
$\dfrac{{90.x}}{{100}} = 0,9.x$ (triệu đồng)
Vậy sau kì hạn 1 năm, số tiền bác Ngọc có được cả gốc lẫn lãi ở ngân hàng thứ nhất là:
90 + 0,9x (triệu đồng)
Vậy sau kì hạn 1 năm, số tiền bác Ngọc có được cả gốc lẫn lãi ở cả hai ngân hàng là:
90 + 0,9x + 0,8x + 81,2 = (0,9 + 0,8)x + (90 + 81,2) = 1,7x + 171,2(triệu đồng)
Bài 4 trang 59 Toán 7 tập 2 Cánh diều
Người ta rót nước từ một can đựng 10 lít sang một bể rỗng có dạng hình lập phương với độ dài cạnh 20cm. Khi mực nước trong bể cao h (cm) thì thể tích nước trong can còn lại là bao nhiêu? Biết rằng 1 lít =$1d{m^3}.$
Hướng dẫn giải:
Đổi 20 cm = 2 dm;$h cm = \dfrac{h}{10} dm.$
Thể tích của chiếc bể tính đến độ cao h là:$2.2.\dfrac{h}{10} = 0,4.h(d{m^3})=0,4.h (lít)$
Vậy khi mực nước trong bể cao h (cm) thì thể tích nước trong can còn lại là:
10 – 0,4.h (lít)
Bài 5 trang 59 Toán 7 tập 2 Cánh diều
Bạn Minh cho rằng “Tổng của hai đa thức bậc bốn luôn luôn là đa thức bậc bốn”. Bạn Quân cho rằng “Hiệu của hai đa thức bậc bốn luôn luôn là đa thức bậc bốn”. Hai bạn Minh và Quân nói như vậy có đúng không? Giải thích vì sao.
Hướng dẫn giải:
* Giả sử, cho hai đa thức biết:
– Trong đa thức thứ nhất: hệ số a của đơn thức$a{x^4}.$
– Trong đa thức thứ hai: hệ số – a của đơn thức$- a{x^4}.$
Như vậy, bậc của tổng của hai đa thức sẽ là bậc 3. (Vì khi cộng hai đa thức với nhau, ta có a + ( – a) = 0 nên biến với số mũ là 4 sẽ không còn).
Vậy bạn Minh nói như vậy là không đúng.
* Giả sử, cho hai đa thức biết:
– Trong đa thức thứ nhất: hệ số a của đơn thức$a{x^4}.$
– Trong đa thức thứ hai: hệ số a của đơn thức$- a{x^4}.$
Như vậy, bậc của hiệu của hai đa thức sẽ là bậc 3. (Vì khi trừ hai đa thức với nhau, ta có a – a = 0 nên biến với số mũ là 4 sẽ không còn).
Vậy bạn Quân nói như vậy là không đúng.
