Giải Toán 7 tập 1 Trang 80 Bài 3: Hai đường thẳng song song

Giải toán 7 tập 1 trang 80 bài 3 sách Chân trời sáng tạo có Hướng dẫn giải chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 7 Chân trời sáng tạo. Mời các em học sinh cùng quý phụ huynh tham khảo.

Giải Toán 7 tập 1 Trang 76

Khởi động trang 76 Toán 7 tập 1

Hai đường thẳng a và b không có điểm nào chung thì được gọi là hai đường thẳng song song và được kí hiệu là a // b hoặc b // a.

– Có dấu hiệu gì về số đo của các góc đỉnh A và các góc đỉnh B trong hình bên để nhận biết hai đường thẳng a và b song song hay không?

Hướng dẫn giải:

Sau khi học bài học ta rút được kết luận:

Để nhận biết hai đường thẳng a và b song song với nhau hay không ta kiểm tra các cặp góc so le trong bằng nhau hoặc các cặp góc đồng vị bằng nhau.

Khám phá 1 trang 76 Toán 7 tập 1

Quan sát Hình 3 và dự đoán các đường thẳng nào song song với nhau.

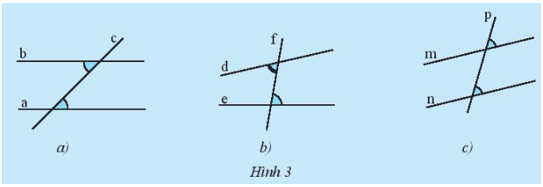
Hướng dẫn giải:

Dự đoán các đường thẳng song song với nhau là:

a // b

m // n

Giải Toán 7 tập 1 Trang 77

Thực hành 1 trang 77 Toán 7 Tập 1

Tìm các cặp đường thẳng song song trong Hình 5 và giải thích.

Hướng dẫn giải

Xét hình a: a // b vì đường thẳng c cắt 2 đường thẳng a, b và tạo thành một cặp góc so le trong bằng nhau

Xét hình b: không có cặp đường thẳng nào song song vì đường thẳng g cắt 2 đường thẳng d, e và không tạo thành một cặp góc so le trong bằng nhau ( 90⁰ khác 80⁰)

Xét hình c: m // n vì đường thẳng p cắt 2 đường thẳng m, n và tạo thành một cặp góc đồng vị bằng nhau

Thực hành 2 trang 77 Toán 7 tập 1 :

Cho hai đường thẳng phân biệt a và b cùng vuông góc với đường thẳng c tại A và B (Hình 6). Hãy chứng tỏ a // b.

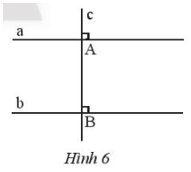
Hướng dẫn giải:

Kí hiệu hình vẽ như sau:

Ta có: a ⊥ c => $\widehat {{A_1}} = {90^0}$

b ⊥ c => $\widehat {{B_1}} = {90^0}$

=> $\widehat {{A_1}} = \widehat {{B_1}} = {90^0}$

Mà hai góc $\widehat {{A_1}};\widehat {{B_1}}$ nằm ở vị trí so le trong

=> a // b

Giải Toán 7 tập 1 Trang 78

Khám phá 2 trang 78 Toán 7 tập 1

Cho điểm A nằm ngoài đường thẳng a, quan sát cách vẽ đường thẳng b đi qua A và song song với a ở Hình 8.

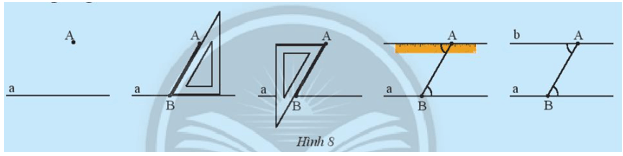
Em hãy dự đoán xem có tất cả bao nhiêu đường thẳng b đi qua A và song song với đường thẳng a.

Hướng dẫn giải:

Vẽ hình theo các bước như trên Hình 8.

Dự đoán: có một đường thẳng b đi qua A và song song với đường thẳng a.

Giải Toán 7 tập 1 Trang 79

Thực hành 3 trang 79 Toán 7 Tập 1

a) Cho tam giác ABC. Hãy nêu cách vẽ đường thẳng a đi qua đỉnh A và song song với BC, cách vẽ đường thẳng b đi qua đỉnh B và song song với AC.

b) Có thể vẽ được bao nhiêu đường thẳng a, bao nhiêu đường thẳng b? Vì sao?

Hướng dẫn giải:

Đo góc ABC. Vẽ đường thẳng a đi qua A sao cho góc tạo bởi a và đường thẳng AB bằng góc ABC.

Ta được đường thẳng a đi qua A và song song với BC

Đo góc ACB. Vẽ đường thẳng b đi qua B sao cho góc tạo bởi b và đường thẳng BC bằng góc ACB.

Ta được đường thẳng b đi qua B và song song với AC

b) Có thể vẽ được chỉ 1 đường thẳng a, 1 đường thẳng b thoả mãn yêu cầu. Vì qua 1 điểm nằm ngoài một đường thẳng, chỉ có 1 đường thẳng song song với nó

Khám phá 3 trang 79 Toán 7 Tập 1

Em hãy:

– Vẽ hai đường thẳng a và b song song với nhau.

– Vẽ đường thẳng c cắt đường thẳng a và b lần lượt tại A và B.

a) Chọn và đo một cặp góc so le trong, so sánh cặp góc này.

b) Chọn và đo một cặp góc đồng vị, so sánh cặp góc này.

Hướng dẫn giải:

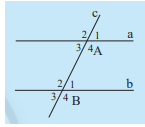
a) Một cặp góc so le trong là góc A3 và góc B1 . Hai góc này cùng có số đo là 60⁰ nên chúng bằng nhau .

b) Một cặp góc đồng vị là góc A1 và góc B1 . Hai góc này cùng có số đo là 60⁰ nên chúng bằng nhau .

Thực hành 4 trang 79 Toán 7 tập 1

Cho biết m // n và a // b. Tính số đo x, y, z, t của các góc trong Hình 12.

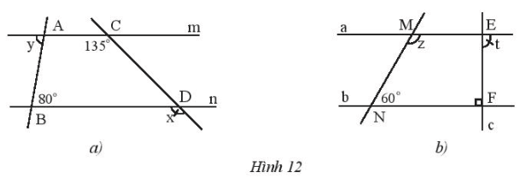
Hướng dẫn giải:

Kí hiệu hình vẽ:

Xét hình 12a

Ta có: m // n

=> $x = \widehat {ACD} = {45^0}$ (Hai góc đồng vị)

Ta cũng có: $y = \widehat {ABD} = {80^0}$ (Hai góc so le trong)

Vậy x = 45⁰; y = 80⁰

Xét hình 12b

Ta có: a // b => $\widehat {{M_1}} = \widehat {MNF} = {60^0}$

Mặt khác: $\widehat {{M_1}} + \widehat {NME} = {180^0}$ (Hai góc kề bù)

=> $\widehat {MNF} = {180^0} – \widehat {{M_1}} = {180^0} – {60^0} = {120^0}$

=> z = 60⁰

Ta có: a // b => $t = \widehat {EFN} = {90^0}$ (Hai góc so le trong)

Giải Toán 7 tập 1 Trang 80

Vận dụng 1 trang 80 Toán 7 tập 1 :

Tìm các cặp góc bằng nhau của hai tam giác ABC và DEC trong Hình 13, biết a // b.

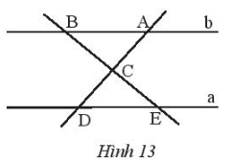
Hướng dẫn giải:

Ta có: a // b

=> $\widehat {CBA} = \widehat {CED}$ ; $\widehat {BAC} = \widehat {EDC}$ (hai góc so le trong)

Ta lại có:

$\widehat {BCA} = \widehat {CDE}$(Hai góc đối đỉnh)

Vậy các cặp góc bằng nhau của tam giác ABC và DEC là $\widehat {CBA} = \widehat {CED}$; $\widehat {BAC} = \widehat {EDC}$; $\widehat {BCA} = \widehat {CDE}$

Vận dụng 2 trang 80 Toán 7 tập 1

Cho hai đường thẳng a, b song song với nhau, đường thẳng c vuông góc với a tại A và cắt b tại B. Hãy giải thích tại sao đường thẳng c cũng vuông góc với b.

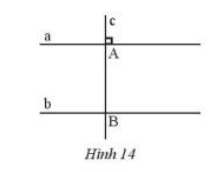
Hướng dẫn giải:

Kí hiệu hình vẽ như sau:

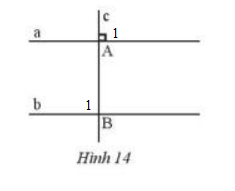
Ta có: a // b => $\widehat {{A_1}} = \widehat {{B_1}}$ (Hai góc so le trong) (1)

Do đường thẳng c vuông góc với đường thẳng a

=> $\widehat {{A_0}} = {90^0}$ (2)

Từ (1) và (2) => $\widehat {{A_1}} = \widehat {{B_1}} = {90^0}$

=> $c \bot b$

Vậy đường thẳng c cũng vuông góc với đường thẳng b.

Giải bài 1 trang 80 Toán 7 tập 1

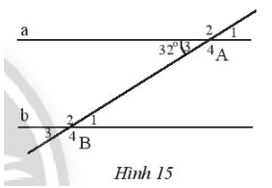
Trong Hình 15, cho biết a // b, Tìm số đo các góc đỉnh A và B

Hướng dẫn giải:

Hướng dẫn giải:

Ta có:$\widehat {{A_3}} = \widehat {{A_1}}$ (2 góc đối đỉnh), mà $\widehat {{A_3}} = 32^\circ$nên $\widehat {{A_1}} = 32^\circ$

Vì $\widehat {{A_3}} + \widehat {{A_4}} = 180^\circ$(2 góc kề bù) nên $32^\circ + \widehat {{A_4}} = 180^\circ \Rightarrow \widehat {{A_4}} = 180^\circ – 32^\circ = 148^\circ$

Vì $\widehat {{A_2}} = \widehat {{A_4}}$ (2 góc đối đỉnh), mà $\widehat {{A_4}} = 148^\circ$nên $\widehat {{A_2}} = 148^\circ$

Vì a // b nên:

+) $\widehat {{A_3}} = \widehat {{B_1}}$(2 góc so le trong), mà $\widehat {{A_3}} = 32^\circ$nên $\widehat {{B_1}} = 32^\circ$

+) $\widehat {{A_4}} = \widehat {{B_2}}$(2 góc so le trong), mà $\widehat {{A_4}} = 148^\circ$nên $\widehat {{B_2}} = 148^\circ$

+) $\widehat {{A_3}} = \widehat {{B_3}}$ (2 góc đồng vị), mà  $\widehat {{A_3}} = 32^\circ$nên $\widehat {{B_3}} = 32^\circ$

+) $\widehat {{A_4}} = \widehat {{B_4}}$ (2 góc đồng vị), mà $\widehat {{A_4}} = 148^\circ$nên $\widehat {{B_4}} = 148^\circ$

Giải bài 2 trang 80 Toán 7 tập 1

Vẽ một đường thẳng cắt hai đường thẳng sao cho trong các góc tạo thành có một cặp góc so le trong bằng nhau. Đặt tên cho các góc đó.

a) Vì sao cặp góc so le trong còn lại cũng bằng nhau?

b) Vì sao các cặp góc đồng vị cũng bằng nhau?

Hướng dẫn giải:

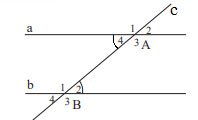
Vì đường thẳng c cắt hai đường thẳng a và b tạo thành một cặp góc so le trong ( góc A4 và B3) bằng nhau nên a // b ( Dấu hiệu nhận biết 2 đường thẳng song song)

Vì a // b nên theo tính chất của 2 đường thẳng song song:

a) Các so le trong bằng nhau

b) Các góc đồng vị bằng nhau

Giải bài 3 trang 80 Toán 7 tập 1

Hãy nói các cách để kiểm tra hai đường thẳng song song mà em biết

Hướng dẫn giải:

Cách 1: Kiểm tra 2 góc ở vị trí so le trong có bằng nhau không. Nếu bằng nhau thì 2 đường thẳng song song.

Cách 2: Kiểm tra 2 góc ở vị trí đồng vị có bằng nhau không. Nếu bằng nhau thì 2 đường thẳng song song.

Cách 3: Kiểm tra 2 đường thẳng có cùng song song với 1 đường thẳng không. Nếu có thì 2 đường thẳng song song.

Cách 4: Kiểm tra 2 đường thẳng có cùng vuông góc với 1 đường thẳng không. Nếu có thì 2 đường thẳng song song.

Giải bài 4 trang 80 Toán 7 tập 1

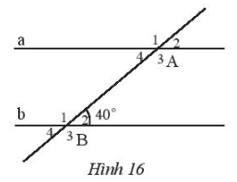
Cho Hình 16, biết a // b.

a) Chỉ ra góc ở vị trí so le trong, đồng vị với góc $\widehat {{B_2}}$

b) Tính số đo các góc$\widehat {{A_4}},\widehat {{A_2}},\widehat {{B_3}}$

c) Tính số đo các góc $\widehat {{B_1}},\widehat {{A_1}}$

Hướng dẫn giải:

a) Góc ở vị trí so le trong với góc $\widehat {{B_2}}$ là: $\widehat {{A_4}}$

Góc ở vị trí đồng vị với góc $\widehat {{B_2}}$ là: $\widehat {{A_2}}$

b) Vì a // b nên:

+)$\widehat {{A_4}} = \widehat {{B_2}}$(2 góc so le trong), mà $\widehat {{B_2}} = 40^\circ$ nên $\widehat {{A_4}} = 40^\circ$

+) $\widehat {{A_2}} = \widehat {{B_2}}$ (2 góc đồng vị), mà  $\widehat {{B_2}} = 40^\circ$nên $\widehat {{A_2}} = 40^\circ$

Ta có: $\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ$(2 góc kề bù) nên $40^\circ + \widehat {{B_3}} = 180^\circ \Rightarrow \widehat {{B_3}} = 180^\circ – 40^\circ = 140^\circ$

c) Ta có: $\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ$(2 góc kề bù) nên $40^\circ + \widehat {{B_1}} = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ – 40^\circ = 140^\circ$

Vì a // b nên $\widehat {{A_1}} = \widehat {{B_1}}$ (2 góc đồng vị) nên $\widehat {{A_1}} = 140^\circ$

Giải bài 5 trang 80 Toán 7 tập 1

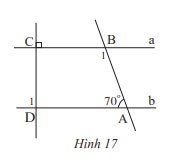
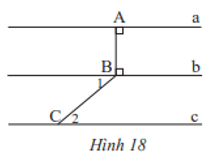
Cho Hình 17, biết a // b.

Tính số đo các góc $\widehat {{B_1}}$ và $\widehat {{D_1}}$

Hướng dẫn giải:

Vì a // b nên

+) $\widehat {{C_1}} = \widehat {{D_2}}$ (2 góc đồng vị), mà  $\widehat {{C_1}} = 90^\circ$ nên $\widehat {{D_2}} = 90^\circ$ . Do đó, $b \bot CD$ nên $\widehat {{D_1}}= 90^\circ$

+) $\widehat {{A_1}} = \widehat {{B_2}}$ (2 góc so le trong) nên $\widehat {{B_2}} = 70^\circ$

Ta có:$\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ$ (2 góc kề bù) nên$\widehat {{B_1}} + 70^\circ = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ – 70^\circ = 110^\circ$

Giải Toán 7 tập 1 Trang 81

Giải bài 6 trang 81 Toán 7 tập 1

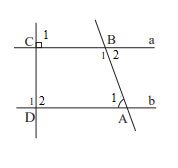
Cho Hình 18, biết $\widehat {{B_1}} = 40^\circ ,\widehat {{C_2}} = 40^\circ$

a) Đường thẳng a có song song với đường thẳng b không? Vì sao?

b) Đường thẳng b có song song với đường thẳng c không? Vì sao?

c) Đường thẳng a có song song với đường thẳng c không? Vì sao

Hướng dẫn giải:

a) Vì a, b cùng vuông góc với đường thẳng AB nên a // b

b) Vì $\widehat {{B_1}} = \widehat {{C_2}}( = 40^\circ )$. Mà 2 góc này ở vị trí so le trong nên b // c (Dấu hiệu nhận biết 2 đường thẳng song song)

c) Vì a // b (câu a) và b // c (câu b).

Nên a // c (cùng song song với đường thẳng b).

Vậy đường thẳng a song song với đường thẳng c.

Giải bài 7 trang 81 Toán 7 tập 1

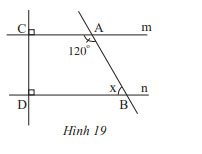
Quan sát Hình 19 và cho biết:

a) Vì sao m // n?

b) Số đo x của góc $\widehat {ABD}$ là bao nhiêu?

Hướng dẫn giải:

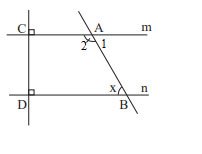
a) Vì m và n cùng vuông góc với BC nên m // n

a) Vì m và n cùng vuông góc với BC nên m // n

b) Ta có: $\widehat {{A_2}} + \widehat {{A_1}} = 180^\circ \Rightarrow 120^\circ + \widehat {{A_1}} = 180^\circ \Rightarrow \widehat {{A_1}} = 180^\circ – 120^\circ = 60^\circ$

Vì m // n nên $\widehat {{A_1}} = \widehat {ABD}$ ( 2 góc so le trong) nên $\widehat {ABD} = 60^\circ$

Vậy $x = 60^\circ$