Luyện tập chung

Giải toán 8 tập 1 trang 88 Bài luyện tập chung sách Kết nối tri thức có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 8 Kết nối tri thức. Mời các em học sinh cùng quý phụ huynh tham khảo.

Toán 8 tập 1 trang 88

Giải bài 4.13 Toán 8 tập 1

Tìm độ dài x trong Hình 4.30

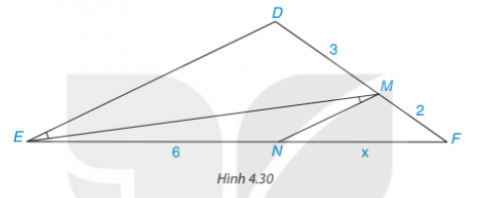
Hướng dẫn giải:

Ta có: $\widehat{NME}=\widehat{MED}$, hai góc ở vị trí so le trong suy ra MN//DE

$\Rightarrow \frac{FN}{NE}=\frac{FM}{MD}$

$\Rightarrow \frac{x}{6}=\frac{2}{3}\Rightarrow x=4$

Giải bài 4.14 Toán 8 tập 1

Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC

a) Chứng minh EF // CD, FK // AB

b) So sánh EF và $\frac{1}{2}(AB+CD)$

Hướng dẫn giải:

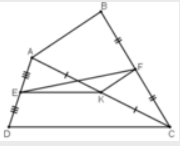
a) Xét ΔADC có

E là trung điểm của AD

K là trung điểm của AC

Do đó: EK là đường trung bình của ΔADC

Suy ra: EK//DC

Xét ΔABC có

K là trung điểm của AC

F là trung điểm của BC

Do đó: KF là đường trung bình của ΔABC

Suy ra: KF//AB

b) EK là đường trung bình của ΔADC suy ra $EK=\frac{CD}{2}$

KF là đường trung bình của ΔABC suy ra $KF=\frac{AB}{2}$

Ta có: $EF\leq EK+KF=\frac{CD}{2}+\frac{AB}{2}=\frac{AB+CD}{2}$

Giải bài 4.15 trang 88 Toán 8 tập 1

Cho tam giác ABC, phân giác AD ($D\in BC$). Đường thẳng qua D song song với AB cắt AC tại E. Chứng minh rằng $\frac{AC}{AB}=\frac{EC}{EA}$

Hướng dẫn giải:

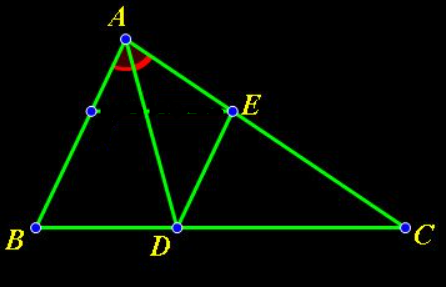
Xét tam giác ABC có AD là phân giác góc A suy ra $\frac{AC}{AB}=\frac{CD}{DB}$ (1)

ED // AB suy ra $\frac{EC}{EA}=\frac{CD}{DB}$ (2)

Từ (1) và (2) $\Rightarrow \frac{AC}{AB}=\frac{EC}{EA}$

Giải bài 4.16 trang 88 Toán 8 tập 1

Tam giác ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt cạnh BC tại D

a) Tính độ dài đoạn thẳng DB và DC

b) Tính tỉ số diện tích của hai tam giác ABD và ACD

Hướng dẫn giải:

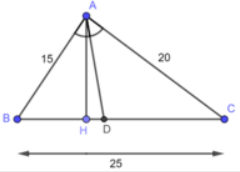
a) Trong tam giác ABC, ta có: AD là đường phân giác góc A

$\Rightarrow \frac{DB}{DC}=\frac{AB}{AC}$

Mà AB = 15 cm và AC = 20 cm (gt)

Nên $\frac{DB}{DC}=\frac{15}{20}$

$\Rightarrow \frac{DB}{DB+DC}=\frac{15}{15+20}$ (tính chất tỉ lệ thức)

$\Rightarrow \frac{DB}{BC}=\frac{15}{35}$

$\Rightarrow  DB=\frac{15}{35}\times BC=\frac{15}{35}\times 25=\frac{75}{7}$ (cm)

b) Kẻ $AH\perp  BC$

Ta có $S_{ABD}=\frac{1}{2}AH\times  BD$

$S _{ACD}=\frac{1}{2}AH\times  CD$

$\Rightarrow \frac{S_{ABD}}{S_{ACD}}=\frac{\frac{1}{2}AH\times BD}{\frac{1}{2}AH\times CD}=\frac{BD}{DC}$

Mà $\frac{DB}{DC}=\frac{15}{12}=\frac{3}{4}$

$\Rightarrow \frac{S_{ABD}}{S_{ACD}}=\frac{3}{4}$$

Giải bài 4.17 trang 88 Toán 8 tập 1

Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo thứ tự tại M, N, K. Chứng minh rằng: $DM^{2}=MN\times MK$

Hướng dẫn giải:

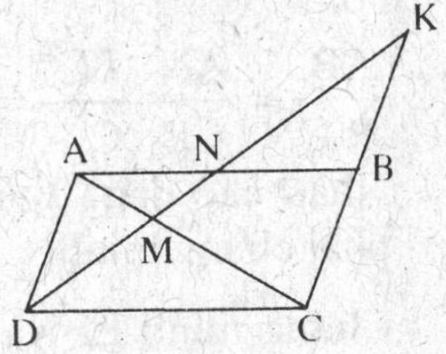
a) AD // BC (ABCD là hình bình hành) $\Rightarrow \frac{DM}{MK}=\frac{MA}{MC}$

AB // CD $\Rightarrow \frac{MA}{MC}=\frac{MN}{DM}$

Suy ra $\frac{DM}{MK}=\frac{MN}{DM}$ hay $DM^{2}=MN\times MK$