Giải toán 8 tập 2 trang 82 Bài 7: Trường hợp đồng dạng thứ hai của tam giác
Giải toán 8 tập 2 trang 82 Bài 7: Trường hợp đồng dạng thứ hai của tam giác
Giải toán 8 tập 2 trang 82 bài 7 sách Cánh diều có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 8 Cánh diều. Mời các em học sinh cùng quý phụ huynh tham khảo.
Giải toán 8 tập 2 trang 79
HĐ1 trang 79 toán 8 tập 2
Quan sát hình 68 và so sánh:
a) Các tỉ số $\frac{{A’B’}}{{AB}}$ và $\frac{{A’C’}}{{AC}}$
b) Các góc $\widehat A$ và $\widehat {A’}$
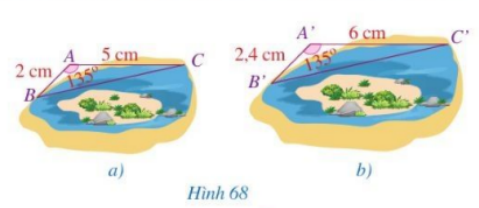
Phương pháp giải:
Quan sát hình và so sánh các góc và tỉ số các cạnh.
Lời giải chi tiết:
a) Ta có:
$\begin{array}{l}\frac{{A’B’}}{{AB}} = \frac{2,4}{{2}} = \frac{6}{5}\\\frac{{A’C’}}{{AC}} = \frac{6}{5}\end{array}$
Vậy $\frac{{A’B’}}{{AB}} = \frac{{A’C’}}{{AC}}$
b) Ta có: $\widehat A = \widehat {A’} = 135^\circ $
LT1 trang 79 toán 8 tập 2
Cho hai tam giác ABC và A’B’C’ thỏa mãn $AB = 2,AC = 3,A’B’ = 6,A’C’ = 9$ và $\widehat A = \widehat {A’}$. Chứng minh $\widehat B = \widehat {B’},\,\,\widehat C = \widehat {C’}$.
Lời giải chi tiết:
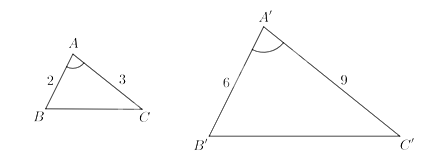
Ta thấy
$\begin{array}{l}\frac{{AB}}{{A’B’}} = \frac{2}{6} = \frac{1}{3}\\\frac{{AC}}{{A’C’}} = \frac{3}{9} = \frac{1}{3}\\ \Rightarrow \frac{{AB}}{{A’B’}} = \frac{{AC}}{{A’C’}}\end{array}$
Xét tam giác ABC và tam giác A’B’C’ có:
$\frac{{AB}}{{A’B’}} = \frac{{AC}}{{A’C’}}$ và $\widehat A = \widehat {A’}$
$ \Rightarrow \Delta ABC \backsim \Delta A’B’C’$ (c-g-c)
$ \Rightarrow $$\widehat B = \widehat {B’},\,\,\widehat C = \widehat {C’}$
Giải toán 8 tập 2 trang 80
LT2 trang 80 toán 8 tập 2
Cho góc $xOy$. Trên tia Ox lấy các điểm A, B sao cho $OA = 2cm,\,\,OB = 9cm$. Trên tia Oy lấy các điểm M, N sao cho $OM = 3cm,\,\,ON = 6cm$. ChỨNG minh $\widehat {OBM} = \widehat {ONA}$.
Lời giải chi tiết:

Ta thấy
$\begin{array}{l}\frac{{OA}}{{OM}} = \frac{2}{3};\,\,\frac{{ON}}{{OB}} = \frac{6}{9} = \frac{2}{3}\\ \Rightarrow \frac{{OA}}{{OM}} = \frac{{ON}}{{OB}}\end{array}$
Xét tam giác OAN và tam giác OMB có:
$\frac{{OA}}{{OM}} = \frac{{ON}}{{OB}}$ và $\widehat O$ chung
$ \Rightarrow \Delta OAN \backsim \Delta OMB$ (c-g-c)
$ \Rightarrow \widehat {OBM} = \widehat {ONA}$
HĐ2 trang 81 toán 8 tập 2
Cho hai tam giác ABC và A’B’C’ có $\widehat {A’} = \widehat A = 90^\circ ,\,\,\frac{{A’B’}}{{AB}} = \frac{{A’C’}}{{AC}}$ (Hình 72). Chứng minh $\Delta A’B’C’ \backsim \Delta ABC$
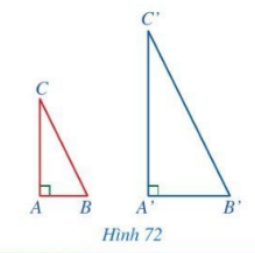
Phương pháp giải:
Dựa vào trường hợp đồng dạng thứ hai để chứng minh hai tam giác đồng dạng.
Lời giải chi tiết:
Xét tam giác A’B’C’ và tam giác ABC có:
$\frac{{A’B’}}{{AB}} = \frac{{A’C’}}{{AC}}$ và $\widehat {A’} = \widehat A = 90^\circ $
$ \Rightarrow \Delta A’B’C’ \backsim \Delta ABC$ (c-g-c)
Giải toán 8 tập 2 trang 81
LT3 trang 81 toán 8 tập 2
Cho hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ sao cho $\frac{{AB}}{{AC}} = \frac{{A’B’}}{{A’C’}}$. Chứng minh $\widehat B = \widehat {B’}$.
Lời giải chi tiết:
Ta có: $\frac{{AB}}{{AC}} = \frac{{A’B’}}{{A’C’}} \Rightarrow \frac{{AB}}{{A’B’}} = \frac{{AC}}{{A’C’}}$
Hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ nên $\widehat {A’} = \widehat A = 90^\circ $.
Xét tam giác ABC và tam giác A’B’C’ có:
$\frac{{AB}}{{A’B’}} = \frac{{AC}}{{A’C’}}$ và $\widehat {A’} = \widehat A$
$ \Rightarrow \Delta ABC \backsim \Delta A’B’C’$ (c-g-c)
$ \Rightarrow \widehat B = \widehat {B’}$.
Giải Bài 1 trang 81 Toán 8 Cánh diều tập 2
Cho Hình 74.
a) Chứng minh $\triangle$ABC $\sim$ $\triangle$MNP.
b) Góc nào của tam giác MNP bằng góc B?
c) Góc nào của tam giác ABC bằng góc P?
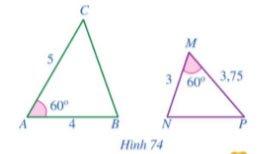
Hướng dẫn giải
a) Ta có: $\frac{AB}{MN}=\frac{4}{3}$; $\frac{CA}{PM}=\frac{5}{3,75}=\frac{4}{3}$
Suy ra: $\frac{AB}{MN}=\frac{CA}{PM}$ mà $\widehat{A}=\widehat{M}=60^{\circ}$
Do đó: $\triangle$ABC $\sim$ $\triangle$MNP.
b) Góc N của tam giác MNP bằng góc B.
c) Góc C của tam giác ABC bằng góc P.
Giải toán 8 tập 2 trang 82
Giải Bài 2 trang 82 Toán 8 Cánh diều tập 2
Cho Hình 75, chứng minh:
a) $\triangle$IAB $\sim$ $\triangle$IDC;
b) $\triangle$IAD $\sim$ $\triangle$IBC.
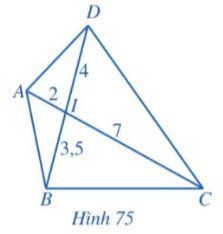
Hướng dẫn giải
a) Ta có: $\frac{IA}{ID}=\frac{2}{4}=\frac{1}{2}$; $\frac{IB}{IC}=\frac{3,5}{7}=\frac{1}{2}$
Suy ra: $\frac{IA}{ID}=\frac{IB}{IC}$
Mà $\widehat{AIB}=\widehat{DIC}$ (hai góc đối đỉnh)
Do đó: $\triangle$IAB $\sim$ $\triangle$IDC (c.g.c).
b) Ta có: $\frac{IA}{IB}=\frac{2}{3,5}=\frac{4}{7}$; $\frac{ID}{IC}=\frac{4}{7}$
Suy ra: $\frac{IA}{IB}=\frac{ID}{IC}$
Mà $\widehat{AID}=\widehat{BIC}$ (hai góc đối đỉnh)
Do đó: $\triangle$IAD $\sim$ $\triangle$IBC (c.g.c)
Giải Bài 3 trang 82 Toán 8 Cánh diều tập 2
Cho Hình 76, biết AB = 4, BC = 3, BE = 2, BD = 6. Chứng minh:
a) $\triangle$ABD $\sim$ $\triangle$EBC;
b) $\widehat{DAB}=\widehat{DEG}$;
c) Tam giác DGE vuông.
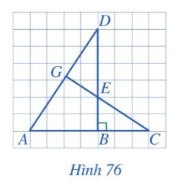
Hướng dẫn giải
a) Ta có: $\frac{AB}{EB}=\frac{4}{2}=2$; $\frac{BD}{BC}=\frac{6}{3}=2$
Suy ra: $\frac{AB}{EB}=\frac{BD}{BC}$
Mà $\widehat{ABD}=\widehat{EBC}=90^{\circ}$
Do đó: $\triangle$ABD $\sim$ $\triangle$EBC (c.g.c).
b) Vì $\triangle$ABD $\sim$ $\triangle$EBC (cmt) nên $\widehat{DAB}=\widehat{CEB}$
Mà $\widehat{CEB}=\widehat{DEG}$ (hai góc đối đỉnh)
Suy ra: $\widehat{DAB}=\widehat{DEG}$.
c) Tam giác DAB vuông tại B có: $\widehat{DAB}+\widehat{D}=90^{\circ}$
Mà $\widehat{DAB}=\widehat{DEG}$ (cmt)
Suy ra: $\widehat{DEG}+\widehat{D}=90^{\circ}$ hay $\widehat{DGE}=90^{\circ}$
Do đó: Tam giác DGE vuông tại G.
Giải Bài 4 trang 82 Toán 8 Cánh diều tập 2
Cho Hình 77, chứng minh:
a) $\widehat{ABC}=\widehat{BED}$;
b) BC $\perp$ BE.
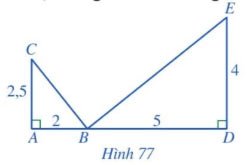
Hướng dẫn giải
a) Ta có: $\frac{AB}{DE}=\frac{2}{4}=\frac{1}{2}$; $\frac{AC}{DB}=\frac{2,5}{5}=\frac{1}{2}$
Suy ra: $\frac{AB}{DE}=\frac{AC}{DB}$
Mà $\widehat{A}=\widehat{D}=90^{\circ}$
Do đó: $\triangle$ABC $\sim$ $\triangle$DEB (c.g.c)
Nên $\widehat{ABC}=\widehat{BED}$.
b) Tam giác BED vuông tại D có: $\widehat{BED}+\widehat{DBE}=90^{\circ}$
Mà $\widehat{ABC}=\widehat{BED}$ (cmt)
Suy ra: $\widehat{ABC}+\widehat{DBE}=90^{\circ}$
Mà $\widehat{CBE}=180^{\circ}-\widehat{ABC}-\widehat{DBE}$
Do đó: $\widehat{CBE}=90^{\circ}$
Hay BC $\perp$ BE.
Giải Bài 5 trang 82 Toán 8 Cánh diều tập 2
Cho $\triangle$ABC $\sim$ $\triangle$MNP.
a) Gọi D và Q lần lượt là trung điểm của BC và NP. Chứng minh $\triangle$ABD $\sim$ $\triangle$MNQ.
b) Gọi G và K lần lượt là trọng tâm của hai tam giác ABC và MNP. Chứng minh $\triangle$ABG $\sim$ $\triangle$MNK.
Hướng dẫn giải
a) Ta có: $\triangle$ABC $\sim$ $\triangle$MNP
Suy ra: $\frac{AB}{MN}=\frac{BC}{NP}$ và $\widehat{B}=\widehat{N}$
Mà BC = 2BD (D là trung điểm BC); NP = 2NQ (Q là trung điểm NP)
Do đó: $\frac{AB}{MN}=\frac{BD}{NQ}$ và $\widehat{B}=\widehat{N}$
Suy ra: $\triangle$ABD $\sim$ $\triangle$MNQ (c.g.c).
b) Ta có: $\triangle$ABD $\sim$ $\triangle$MNQ (cmt)
Suy ra: $\frac{AB}{MN}=\frac{AD}{MQ}$ và $\widehat{BAD}=\widehat{NMQ}$
Mà AD = $\frac{3}{2}$AG (G là trọng tâm tam giác ABC); MQ = $\frac{3}{2}$MK (K là trọng tâm tam giác MNP)
Do đó: $\frac{AB}{MN}=\frac{AG}{MK}$ và $\widehat{BAG}=\widehat{NMK}$
Suy ra: $\triangle$ABG $\sim$ $\triangle$MNK (c.g.c).
Giải Bài 6 trang 82 Toán 8 Cánh diều tập 2
Cho Hình 78, biết $AH^{2}$ = BH.CH. Chứng minh:
a) $\triangle$HAB $\sim$ $\triangle$HCA;
b) Tam giác ABC vuông tại A.

Hướng dẫn giải
a) Ta có: $AH^{2}$ = BH.CH hay $\frac{AH}{CH}=\frac{BH}{AH}$
Mà $\widehat{AHB}=\widehat{CHA}=90^{\circ}$
Do đó: $\triangle$HAB $\sim$ $\triangle$HCA (c.g.c)
b) Do $\triangle$HAB $\sim$ $\triangle$HCA nên $\widehat{HAB}=\widehat{HCA}$ (1)
Tam giác HAC vuông tại H có: $\widehat{HCA}+\widehat{HAC}=90^{\circ}$ (2)
Từ (1)(2) suy ra: $\widehat{HAB}+\widehat{HAC}=90^{\circ}$
Do đó: $\widehat{BAC}=90^{\circ}$
Nên tam giác ABC vuông tại A.
Giải Bài 7 trang 82 Toán 8 Cánh diều tập 2
Đố. Chỉ sử dụng thước thẳng có chia đơn vị đến milimét và thước đo góc, làm thế nào đo được khoảng cách giữa hai vị trí B, C trên thực tế, biết rằng có vị trí A thỏa mãn AB = 20 m, AC = 50 m, $\widehat{BAC}=135^{\circ}$.
Bạn Vy làm như sau: Vẽ tam giác A’B’C’ có A’B’ = 2 cm, A’C’ = 5 cm, $\widehat{B’A’C’}=135^{\circ}$. Bạn Vy lấy thước đo khoảng cách giữa hai điểm B’, C’ và nhận được kết quả B’C’ $\approx$ 6,6 cm. Từ đó, bạn Vy kết luận khoảng cách giữa hai vị trí B, C trên thực tế khoảng 66 m. Em hãy giải thích tại sao bạn Vy có thể kết luận như vậy.
Hướng dẫn giải
Đổi 20 m = 2000 cm; 50 m = 5000 cm
Ta có: $\frac{AB}{A’B’}=\frac{2000}{2}=1000$; $\frac{AC}{A’C’}=\frac{5000}{5}=1000$
Suy ra: $\frac{AB}{A’B’}=\frac{AC}{A’C’}$
Mà $\widehat{BAC}=\widehat{B’A’C’}=135^{\circ}$
Do đó: $\triangle$ABC $\sim$ $\triangle$A’B’C’ (c.g.c)
Suy ra: $\frac{BC}{B’C’}=1000$ mà B’C’ $\approx$ 6,6 cm
Do đó: BC $\approx$ 6600 cm hay 66 m.
