Giải toán 8 tập 2 trang 54 Bài 2: Đường trung bình của tam giác
Giải toán 8 tập 2 trang 54 Bài 2: Đường trung bình của tam giác
Giải toán 8 tập 2 trang 54 bài 2 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 8 CTST. Mời các em học sinh cùng quý phụ huynh tham khảo.
Giải toán 8 tập 2 trang 52
Khởi động trang 52 toán 8 tập 2
Giữa hai điểm $B$ và $C$ có một hồ nước (xem hình bên). Biết $DE = 45m$. Làm thế nào để tính được khoảng cách giữa hai điểm $B$ và $C$?
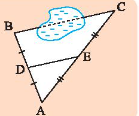
Hướng dẫn giải
Vì $BD = DA \Rightarrow D$ là trung điểm của $AB$;
Vì $EC = EA \Rightarrow E$ là trung điểm của $AC$.
Do đó, $DE$ là đường trung bình của tam giác $ABC$
$ \Rightarrow \left\{ \begin{array}{l}DE//BC\\DE = \frac{1}{2}BC\end{array} \right. \Rightarrow 45 = \frac{1}{2}BC \Leftrightarrow BC = 45.2 = 90\left( m \right)$
Vậy khoảng các của hai điểm $B$ và $C$ là 90 m.
HĐ1 trang 52 toán 8 tập 2
Cho tam giác $ABC$, vẽ đường thẳng $d$ đi qua trung điểm $M$ của cạnh $AB$, song song với cạnh $BC$ và cắt $AC$ tại $N$ (Hình 1). Hãy chứng minh $N$ là trung điểm của $AC$.
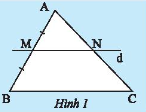
Hướng dẫn giải:
Xét tam giác $ABC$ có $MN//BC$ nên áp dụng định lí Thales cho tam giác ta có:
$\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}$.
Mà $M$ là trung điểm của $AB$ nên $AM = \frac{1}{2}BC$ hay $\frac{{AM}}{{BC}} = \frac{1}{2}$.
Do đó, $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow \frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow AN = \frac{1}{2}AC$.
Do đó, $N$ là trung điểm của $AC$.
THựC HÀNH 1 trang 52 toán 8 tập 2
Tìm độ dài đoạn thẳng $NQ$ trong Hình 4.
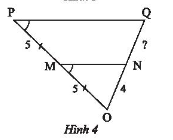
Hướng dẫn giải:
Từ hình vẽ ta có: $\widehat {OMN} = \widehat {OPQ}$.
Mà hai góc này ở vị trí đồng vị nên $MN//PQ$
Xét tam giác $OPQ$ có $MN//PQ$ nên áp dụng định lí Thales cho tam giác ta có:
$\frac{{OM}}{{MP}} = \frac{{ON}}{{NQ}} \Leftrightarrow \frac{5}{5} = \frac{4}{{NQ}} \Rightarrow NQ = \frac{{4.5}}{5} = 4$.
Vậy $NQ = 4$.
Giải toán 8 tập 2 trang 53
VậN DụNG 1 trang 53 toán 8 tập 2
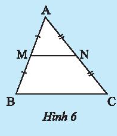
Trong Hình 5, chứng minh $MN$ là đường trung bình của tam giác $ABC$.
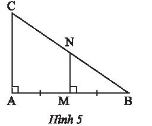
Hướng dẫn giải:
Vì $\left\{ \begin{array}{l}MN \bot AB\\CA \bot AB\end{array} \right. \Rightarrow MN//CA$ (Quan hệ từ vuông góc đến song song).
Ta có:
$AM = BM \Rightarrow BM = \frac{1}{2}AB \Leftrightarrow \frac{{BM}}{{AB}} = \frac{1}{2}$ hay $M$ là trung điểm của $AB$.
Xét tam giác $ABC$ có $NM//AC;MN$ cắt $BA;BC$ lần lượt tại $M;N$. Theo hệ quả của định lí Thales ta có:
$\frac{{BM}}{{AB}} = \frac{{BN}}{{BC}} \Leftrightarrow \frac{{BN}}{{BC}} = \frac{1}{2}$
Hay $2BN = BC$. Do đó, $N$ là trung điểm của $BC$.
Xét tam giác $ABC$ có:
$M$ là trrung điểm của $AB$
$N$ là trrung điểm của $BC$
Do đó, $MN$ là đường trung bình của tam giác $ABC$ (điều phải chứng minh).
HOạT ĐộNG 2 trang 53 toán 8 tập 2
Cho $M,N$ lần lượt là trung điểm của hai cạnh $AB;AC$ của tam giác $ABC$.
a) Tính các tỉ số $\frac{{AM}}{{AB}},\frac{{AN}}{{AC}}$;
b) Cứng mình $MN//BC$;
c) Chứng minh $\frac{{MN}}{{BC}} = \frac{1}{2}$.
Hướng dẫn giải:
a) Vì $AM = MB \Rightarrow M$ là trung điểm của $AB$ (do $M$ thuộc $AB$)
$ \Rightarrow AM = \frac{1}{2}AB \Leftrightarrow \frac{{AM}}{{AB}} = \frac{1}{2}$;
Vì $AN = NC \Rightarrow N$ là trung điểm của $AC$ (do $N$ thuộc $AC$)
$ \Rightarrow AN = \frac{1}{2}AC \Leftrightarrow \frac{{AN}}{{AC}} = \frac{1}{2}$.
b) Vì $\frac{{AM}}{{AB}} = \frac{1}{2};\frac{{AN}}{{AC}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}$.
Xét tam giác $ABC$ có $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}$ nên áp dụng định lí Thales đảo ta được $MN//BC$.
c) Xét tam giác $ABC$ có $MN//BC$ nên áp dụng hệ quả định lí Thales ta được $\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}$
Mà $\frac{{AM}}{{AB}} = \frac{1}{2} \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}$.
Vậy $\frac{{MN}}{{BC}} = \frac{1}{2}$ (điều phải chứng minh).
THựC HÀNH 2 trang 53 toán 8 tập 2
Trong Hình 8, cho biết $JK = 10cm;DE = 6,5cm;EL = 3,7cm$. Tính $DJ;EF;DF;KI$.
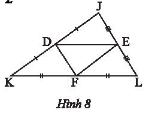
Hướng dẫn giải:
Vì $DJ = KD \Rightarrow D$ là trung điểm của $JK$
$ \Rightarrow DJ = DK = \frac{1}{2}JK = \frac{1}{2}.10 = 5cm$;
Vì $EJ = EL \Rightarrow E$ là trung điểm của $JL$.
$ \Rightarrow 2EL = JL \Leftrightarrow JL = 2.3,7 = 7,4cm$.
Vì $KF = LF \Rightarrow F$ là trung điểm của $KL$.
– Vì $D$ là trung điểm của $JK$; $E$ là trung điểm của $JL$ nên $ED$ là đường trung bình của tam giác $JLK$$ \Rightarrow ED = \frac{1}{2}KL$ (tính chất đường trung bình)
Do đó, $KL = 2ED = 2.6,5 = 13cm$;
– Vì $E$ là trung điểm của $JL$; $F$ là trung điểm của $KL$ nên $EF$ là đường rung bình của tam giác $JLK$$ \Rightarrow EF = \frac{1}{2}JK$ (tính chất đường trung bình)
$ \Leftrightarrow EF = \frac{1}{2}.10 = 5cm$.
– Vì $D$ là trung điểm của $KJ$; $F$ là trung điểm của $KL$ nên $DF$ là đường rung bình của tam giác $JLK$$ \Rightarrow DF = \frac{1}{2}JL$ (tính chất đường trung bình)
$ \Leftrightarrow DF = \frac{1}{2}.7,4 = 3,7cm$.
Vậy $DJ = 5cm;EF = 5cm;DF = 3,7cm;KL = 13cm$
VậN DụNG 2 trang 53 toán 8 tập 2
Hãy tính khoảng cách $BC$ trong phần câu hỏi khởi động trang 52.
Hướng dẫn giải:
Vì $BD = DA \Rightarrow D$ là trung điểm của $AB$;
Vì $EC = EA \Rightarrow E$ là trung điểm của $AC$.
Do đó, $DE$ là đường trung bình của tam giác $ABC$
$ \Rightarrow \left\{ \begin{array}{l}DE//BC\\DE = \frac{1}{2}BC\end{array} \right.$ (tính chất đường trung bình).
$ \Rightarrow 45 = \frac{1}{2}BC \Leftrightarrow BC = 45.2 = 90\left( m \right)$
Vậy khoảng các của hai điểm $B$ và $C$ là 90 m.
Bài 1 trang 53 Toán 8 Tập 2:
Cho MN là đường trung bình của mỗi tam giác ABC trong Hình 9. Hãy tìm giá trị x trong mỗi hình.
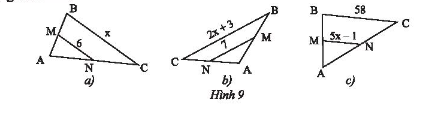
Hướng dẫn giải
– Hình a:
Vì $MN$ là đường trung bình của tam giác $ABC$ nên theo tính chất đường trung bình ta có:
$\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}x \Leftrightarrow 6 = \frac{1}{2}x \Leftrightarrow x = 6:\frac{1}{2} = 12$
– Hình b:
Vì $MN$ là đường trung bình của tam giác $ABC$ nên theo tính chất đường trung bình ta có:
$\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}\left( {2x + 3} \right) \Leftrightarrow 7 = \frac{1}{2}\left( {2x + 3} \right) \Leftrightarrow \left( {2x + 3} \right) = 7:\frac{1}{2} = 14$
$ \Rightarrow 2x = 14 – 3 \Leftrightarrow 2x = 11 \Leftrightarrow x = 5,5$.
– Hình c
Vì $MN$ là đường trung bình của tam giác $ABC$ nên theo tính chất đường trung bình ta có:
$\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}.58 \Leftrightarrow \left( {5x – 1} \right) = \frac{1}{2}.58$
$ \Leftrightarrow \left( {5x – 1} \right) = 29 \Leftrightarrow 5x = 30 \Leftrightarrow x = 30:5 \Leftrightarrow x = 6$.
Giải toán 8 tập 2 trang 54
Giải Bài 2 trang 54 Toán 8 Tập 2:
Tính độ dài đoạn PQ (Hình 10).
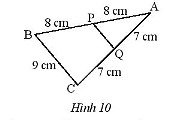
Hướng dẫn giải
Vì $PA = 8cm;PB = 8cm \Rightarrow PA = PB \Rightarrow P$ là trung điểm của $AB$.
Vì $CQ = 7cm;AQ = 7cm \Rightarrow CQ = AQ \Rightarrow Q$ là trung điểm của $AC$.
Xét tam giác $ABC$ có:
$P$ là trung điểm của $AB$; $Q$ là trung điểm của $AC$ nên $PQ$ là đường trung bình của tam giác $ABC$.
$ \Rightarrow PQ = \frac{1}{2}BC$ (tính chất đường trung bình)
$ \Leftrightarrow PQ = \frac{1}{2}.9 = 4,5cm$.
Vậy $PQ = 4,5cm$.
Giải Bài 3 trang 54 toán 8 tập 2
Cho biết cạnh mỗi ô vuông bằng $1cm$. Tính độ dài các đoạn $PQ,PR,RQ,AB,BC,CA$ trong Hình 11.

Hướng dẫn giải
Đoạn thẳng $AB$ là đường chéo của hình chữ nhật với chiều dài là $4cm;$ chiều rộng là $2cm$. Áp dụng định lí Py – ta – go ta được: $A{B^2} = {2^2} + {4^2} = 4 + 16 = 20 \Rightarrow AB = \sqrt {20} = 2\sqrt 5 $
Đoạn thẳng $AC$ là đường chéo của hình chữ nhật với chiều dài là $4cm;$ chiều rộng là $2cm$. Áp dụng định lí Py – ta – go ta được: $A{C^2} = {2^2} + {4^2} = 4 + 16 = 20 \Rightarrow AC = \sqrt {20} = 2\sqrt 5 $
Đoạn thẳng $BC$ là đường chéo của hình chữ nhật với chiều dài là $6cm;$ chiều rộng là $2cm$. Áp dụng định lí Py – ta – go ta được: $B{C^2} = {2^2} + {6^2} = 4 + 36 = 40 \Rightarrow BC = \sqrt {40} = 2\sqrt {10} $
Từ hình vẽ ta thấy:
$Q$ là trung điểm của $AC$;
$R$ là trung điểm của $AB$;
$P$ là trung điểm của $BC$.
– Vì $Q$ là trung điểm của $AC$; $R$ là trung điểm của $AB$ nên $QR$ là đường trung bình của tam giác $ABC \Rightarrow QR = \frac{1}{2}BC$ (tính chất đường trung bình)
$ \Leftrightarrow QR = \frac{1}{2}.2\sqrt {10} = \sqrt {10} \left( {cm} \right)$.
– Vì $Q$ là trung điểm của $AC$; $P$ là trung điểm của $BC$ nên $QP$ là đường trung bình của tam giác $ABC \Rightarrow QP = \frac{1}{2}AB$ (tính chất đường trung bình)
$ \Leftrightarrow QP = \frac{1}{2}.2\sqrt 5 = \sqrt 5 \left( {cm} \right)$.
– $R$ là trung điểm của $AB$; $P$ là trung điểm của $BC$ nên $RP$ là đường trung bình của tam giác $ABC \Rightarrow RP = \frac{1}{2}AC$ (tính chất đường trung bình)
$ \Leftrightarrow RP = \frac{1}{2}.2\sqrt 5 = \sqrt 5 \left( {cm} \right)$.
Giải Bài 4 trang 54 toán 8 tập 2
Cho hình thang $ABCD\left( {AB//CD} \right)$ có $E$ và $F$ lần lượt là trung điểm hai cạnh bên $AD$ và $BC$. Gọi $K$là giao điểm của $AF$ và $DC$ (Hình 12).
a) Tam giác $FBA$ và tam giác $FCK$ có bằng nhau không? Vì sao?
b) Chứng minh: $EF//CD//AB$.
c) Chứng minh $EF = \frac{{AB + CD}}{2}$.

Hướng dẫn giải
a) Vì $K$là giao điểm của $AF$ và $DC$ nên $K \in CD$.
Vì $ABCD$ là hình thang nên $AB//CD \Rightarrow AB//CK$.
Xét tam giác $ABF$ có $CK//AB$ ta có:
$\frac{{FA}}{{FK}} = \frac{{FB}}{{FC}}$ (hệ quả của định lí Thales)
Mà $F$ lần lượt là trung điểm $BC$ nên $\frac{{FB}}{{FC}} = 1 \Rightarrow \frac{{FA}}{{FK}} = 1 \Rightarrow FA = FK$
Xét tam giác $ABF$ và tam giác $KCF$ có:
$FB = FC$ (chứng minh trên)
$FK = FA$ (chứng minh trên)
$\widehat {{F_1}} = \widehat {{F_2}}$
Do đó, tam giác $ABF$ bằng tam giác $KCF$ (c – g – c).
b) Vì $E$ là trung điểm của $AD$;$F$ là trung điểm của $BC$ nên $EF$ là đường trung bình của tam giác $ADK$.
Do đó, $EF//DK$ (tính chất)$ \Rightarrow EF//DC$
Mà $AB//CD \Rightarrow EF//AB//CD$ (điều phải chứng minh).
c) Vì $EF$ là đường trung bình của tam giác $ADK$ nên $EF = \frac{1}{2}DK$.
Tam giác $ABF$ bằng tam giác $KCF$ nên $AB = CK$ (hai cạnh tương ứng)
Ta có: $DK = DC + CK \Rightarrow DK = DC + AB$.
Do đó, \[EF = \frac{1}{2}DK = \frac{1}{2}\left( {DC + AB} \right) = \frac{{DC + AB}}{2}\] (điều phải chứng minh).
Giải Bài 5 trang 54 Toán 8 Tập 2:
Cho tam giác ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.
Hướng dẫn giải
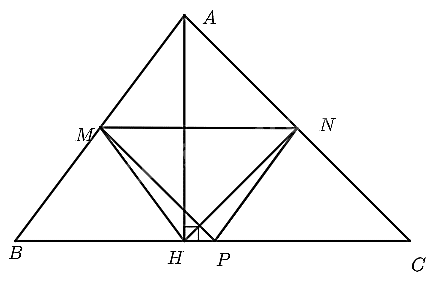
Xét tam giác ABC ta có:
M là trung điểm của AB (gt);
N là trung điểm của AC (gt);
Do đó MN là đường trung bình của tam giác ABC nên MN // BC.
Suy ra tứ giác MNPH là hình thang.
Xét tam giác ABC ta có:
M là trung điểm của AB (gt);
P là trung điểm của BC;
Do đó MP là đường trung bình của tam giác ABC nên MN=$\frac{1}{2}$AC
Vì ΔACH vuông tại H có HN là trung tuyến (N là trung điểm của AC) nên NH=$\frac{1}{2}$AC
Mà MP=$\frac{1}{2}$AC (cmt) nên NH = MP.
Hình thang MNPH (MN // PH) có MP = NH nên là hình thang cân.
Giải Bài 6 trang 54 Toán 8 Tập 2:
Một mái nhà được vẽ lại như Hình 13. Tính độ dài x trong hình mái nhà.
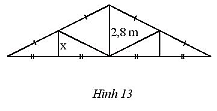
Hướng dẫn giải
Vẽ lại hình và đặt tên các điểm ta được như sau:
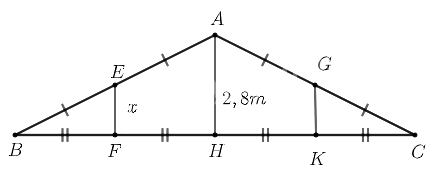
Theo hình vẽ ta có:
$BE = EA \Rightarrow E$ là trung điểm của $AB$;
$BF = FH \Rightarrow F$ là trung điểm của $BH$.
Vì $E$là trung điểm của $AB$; $F$là trung điểm của $BH$ nên $EF$ là đường trung bình của tam giác $ABH$.
$ \Rightarrow EF = \frac{1}{2}AH$ (tính chất đường trung bình)
$ \Leftrightarrow EF = \frac{1}{2}.2,8 = 1,4$.
Vậy $x = 1,4m$.
Giải Bài 7 trang 54 Toán 8 Tập 2:
Ảnh chụp từ Google Maps của một trường học được cho trong Hình 14. Hãy tính chiều dài cạnh DE, cho biết BC = 232 m và B, C lần lượt là trung điểm AD và AE.
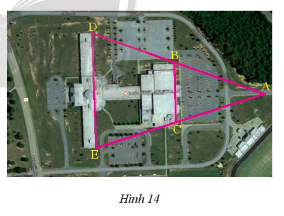
Hướng dẫn giải
Xét tam giác $ADE$ có:
$B,C$ lần lượt là trung điểm của $AD$ và $AE$
$ \Rightarrow BC$ là đường trung bình của tam giác $ADE$.
$ \Rightarrow BC = \frac{1}{2}DE$ (tính chất đường trung bình của tam giác).
$ \Leftrightarrow DE = 2BC = 2.232 = 464\left( m \right)$
Vậy chiều dài cạnh $DE$ là $464m$.
