Giải Toán 11 tập 1 trang 50 bài 1: Dãy số
Giải Toán 11 tập 1 trang 50 bài 1: Dãy số
Giải toán 11 tập 1 trang 50 Bài 1 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 11 Chân trời sáng tạo. Mời các em học sinh cùng quý phụ huynh tham khảo.
Giải Toán 11 tập 1 trang 45
Hoạt động 1 trang 45 Toán 11 tập 1
$u:{\mathbb{N}^*} \to \mathbb{R}$
$n \mapsto {u(n)} = {n^2}$
Tính $u\left( 1 \right);u\left( 2 \right);u\left( {50} \right);u\left( {100} \right)$.
Lời giải:
$\begin{array}{l}u\left( 1 \right) = {1^2} = 1\\u\left( 2 \right) = {2^2} = 4\\u\left( {50} \right) = {50^2} = 2500\\u\left( {100} \right) = {100^2} = 10000\end{array}$
Hoạt động 2 trang 46 Toán 11 tập 1
Cho hàm số:
$v:\left\{ {1;2;3;4;5} \right\} \to \mathbb{R}$
$n \to {\rm{ }}v\left( n \right) = 2n$
Tính $v\left( 1 \right),v\left( 2 \right),v\left( 3 \right),v\left( 4 \right),v\left( 5 \right)$.
Lời giải:
$\begin{array}{l}v\left( 1 \right) = 2.1 = 2\\v\left( 2 \right) = 2.2 = 4\\v\left( 3 \right) = 2.3 = 6\\v\left( 4 \right) = 2.4 = 8\\v\left( 5 \right) = 2.5 = 10\end{array}$
Giải Toán 11 tập 1 trang 46
Thực hành 1 trang 46 Toán 11 tập 1
Cho dãy số:
$u:{\mathbb{N}^*} \to \mathbb{R}$
$n \mapsto {u_n} = {n^3}$
a) Hãy cho biết dãy số trên là hữu hạn hay vô hạn.
b) Viết năm số hạng đầu tiên của dãy số đã cho.
Lời giải:
a) Vì hàm số $u$ xác định trên tập hợp các số nguyên dương ${\mathbb{N}^*}$ nên nó là một dãy số vô hạn.
b) Ta có:
$\begin{array}{l}{u_1} = {1^3} = 1\\{u_2} = {2^3} = 8\\{u_3} = {3^3} = 27\\{u_4} = {4^3} = 64\\{u_5} = {5^3} = 125\end{array}$
Vận dụng 1 trang 46 Toán 11 tập 1
Cho 5 hình tròn theo thứ tự có bán kính 1; 2; 3; 4; 5.
a) Viết dãy số chỉ diện tích của 5 hình tròn này.
b) Tìm số hạng đầu và số hạng cuối của dãy số trên.
Lời giải:
a) Gọi $\left( {{S_n}} \right)$ là dãy số chỉ diện tích của 5 hình tròn với ${S_n} = \pi {n^2}$. Ta có:
$\begin{array}{l}{S_1} = \pi {.1^2} = \pi \\{S_2} = \pi {.2^2} = 4\pi \\{S_3} = \pi {.3^2} = 9\pi \\{S_4} = \pi {.4^2} = 16\pi \\{S_5} = \pi {.5^2} = 25\pi \end{array}$
Vậy dãy số chỉ diện tích của 5 hình tròn là: $\pi ;4\pi ;9\pi ;16\pi ;25\pi $.
b) Số hạng đầu: ${S_1} = \pi $; số hạng cuối: ${S_5} = 25\pi $.
Hoạt động 3 trang 46 Toán 11 tập 1
Cho các dãy số $\left( {{a_n}} \right),\left( {{b_n}} \right),\left( {{c_n}} \right),\left( {{d_n}} \right)$ được xác định như sau.
• ${a_1} = 0;{a_2} = 1;{a_3} = 2;{a_4} = 3;{a_5} = 4$.
• ${b_n} = 2n$.
• $\left\{ \begin{array}{l}{c_1} = 1\\{c_n} = {c_{n – 1}} + 1\left( {n \ge 2} \right)\end{array} \right.$.
• ${d_n}$ là chu vi của đường tròn có bán kính $n$.
Tìm bốn số hạng đầu tiên của các dãy số trên.
Lời giải:
Ta có:
${a_1} = 0;{a_2} = 1;{a_3} = 2;{a_4} = 3;{a_5} = 4$.
${b_1} = 2.1 = 2;{b_2} = 2.2 = 4;{b_3} = 2.3 = 6;{b_4} = 2.4 = 8$.
${c_1} = 1;{c_2} = {c_1} + 1 = 1 + 1 = 2;{c_3} = {c_2} + 1 = 2 + 1 = 3;{c_4} = {c_3} + 1 = 3 + 1 = 4$.
+ Chu vi đường tròn có bán kính $n$ là ${d_n} = 2\pi n$.
Ta có: ${d_1} = 2\pi .1 = 2\pi ;{d_2} = 2\pi .2 = 4\pi ;{d_3} = 2\pi .3 = 6\pi ;{d_4} = 2\pi .4 = 8\pi $.
Giải Toán 11 tập 1 trang 47
Thực hành 2 trang 47 Toán 11 tập 1
Cho dãy số $\left( {{u_n}} \right)$ xác định bởi: $\left\{ \begin{array}{l}{u_1} = 3\\{u_{n + 1}} = 2{u_n}\left( {n \ge 1} \right)\end{array} \right.$.
a) Chứng minh ${u_2} = 2.3;{u_3} = {2^2}.3;{u_4} = {2^3}.3$.
b) Dự đoán công thức số hạng tổng quát của dãy số $\left( {{u_n}} \right)$.
Lời giải:
a) Ta có: ${u_2} = 2{u_1} = 2.3;{u_3} = 2{u_2} = 2.2.3 = {2^2}.3;{u_4} = 2{u_3} = {2.2^2}.3 = {2^3}.3$
b) ${u_n} = {2^{n – 1}}.3$.
Vận dụng 2 trang 47 Toán 11 tập 1
Một chồng cột gỗ được xếp thành các lớp, hai lớp liên tiếp hơn kém nhau 1 cột gỗ (Hình 1). Gọi ${u_n}$ là số cột gỗ nằm ở lớp thứ 2 tính từ trên xuống và cho biết lớp trên cùng có 14 cột gỗ. Hãy xác định dãy số $\left( {{u_n}} \right)$ bằng hai cách:
a) Viết công thức số hạng tổng quát ${u_n}$.
b) Viết hệ thức truy hồi.

Lời giải:
a) Ta có:
$\begin{array}{l}{u_1} = 14 = 13 + 1\\{u_2} = 15 = 13 + 2\\{u_3} = 16 = 13 + 3\\ \vdots \end{array}$
Vậy công thức số hạng tổng quát: ${u_n} = 13 + n$.
b) Ta có:
$\begin{array}{l}{u_1} = 14\\{u_2} = 15 = {u_1} + 1\\{u_3} = 16 = {u_2} + 1\\ \vdots \end{array}$
Vậy công thức truy hồi: ${u_n} = {u_{n – 1}} + 1\left( {n \ge 2} \right)$.
Giải Toán 11 tập 1 trang 48
Hoạt động 4 trang 48 Toán 11 tập 1
Cho hai dãy số $\left( {{a_n}} \right)$ và $\left( {{b_n}} \right)$ được xác định như sau: ${a_n} = 3n + 1;$ ${b_n} = – 5n$.
a) So sánh ${a_n}$ và ${a_{n + 1}},\forall n \in {\mathbb{N}^*}$.
b) So sánh ${b_n}$ và ${b_{n + 1}},\forall n \in {\mathbb{N}^*}$.
Lời giải:
a) Ta có: ${a_{n + 1}} = 3\left( {n + 1} \right) + 1 = 3n + 3 + 1 = 3n + 4$
Xét hiệu: ${a_{n + 1}} – {a_n} = \left( {3n + 4} \right) – \left( {3n + 1} \right) = 3n + 4 – 3n – 1 = 3 > 0,\forall n \in {\mathbb{N}^*}$
Vậy ${a_{n + 1}} > {a_n}$.
a) Ta có: ${b_{n + 1}} = – 5\left( {n + 1} \right) = – 5n – 5$
Xét hiệu: ${b_{n + 1}} – {b_n} = \left( { – 5n – 5} \right) – \left( { – 5n} \right) = – 5n – 5 + 5n = – 5 < 0,\forall n \in {\mathbb{N}^*}$
Vậy ${b_{n + 1}} < {b_n}$.
Thực hành 3 trang 48 Toán 11 tập 1
Xét tính tăng, giảm của các dãy số sau:
a) $\left( {{u_n}} \right)$ với ${u_n} = \frac{{2n – 1}}{{n + 1}}$;
b) $\left( {{x_n}} \right)$ với ${x_n} = \frac{{n + 2}}{{{4^n}}}$;
c) $\left( {{t_n}} \right)$ với ${t_n} = {\left( { – 1} \right)^n}.{n^2}$.
Lời giải:
a) Ta có: ${u_{n + 1}} = \frac{{2\left( {n + 1} \right) – 1}}{{\left( {n + 1} \right) + 1}} = \frac{{2n + 2 – 1}}{{n + 1 + 1}} = \frac{{2n + 1}}{{n + 2}}$
Xét hiệu:
$\begin{array}{l}{u_{n + 1}} – {u_n} = \frac{{2n + 1}}{{n + 2}} – \frac{{2n – 1}}{{n + 1}} = \frac{{\left( {2n + 1} \right)\left( {n + 1} \right) – \left( {2n – 1} \right)\left( {n + 2} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\ = \frac{{\left( {2{n^2} + n + 2n + 1} \right) – \left( {2{n^2} – n + 4n – 2} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\ = \frac{{2{n^2} + n + 2n + 1 – 2{n^2} + n – 4n + 2}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} = \frac{3}{{\left( {n + 2} \right)\left( {n + 1} \right)}} > 0,\forall n \in {\mathbb{N}^*}\end{array}$
Vậy ${u_{n + 1}} – {u_n} > 0 \Leftrightarrow {u_{n + 1}} > {u_n}$. Vậy dãy số $\left( {{u_n}} \right)$ là dãy số tăng.
b) Ta có: ${x_{n + 1}} = \frac{{\left( {n + 1} \right) + 2}}{{{4^{n + 1}}}} = \frac{{n + 1 + 2}}{{{{4.4}^n}}} = \frac{{n + 3}}{{{{4.4}^n}}}$
Xét hiệu:
${x_{n + 1}} – {x_n} = \frac{{n + 3}}{{{{4.4}^n}}} – \frac{{n + 2}}{{{4^n}}} = \frac{{n + 3 – 4\left( {n + 2} \right)}}{{{{4.4}^n}}} = \frac{{n + 3 – 4n – 8}}{{{{4.4}^n}}} = \frac{{ – 3n – 5}}{{{{4.4}^n}}} < 0,\forall n \in {\mathbb{N}^*}$
Vậy ${x_{n + 1}} – {x_n} < 0 \Leftrightarrow {x_{n + 1}} < {x_n}$. Vậy dãy số $\left( {{x_n}} \right)$ là dãy số giảm.
c) Ta có: ${t_1} = {\left( { – 1} \right)^1}{.1^2} = – 1;{t_2} = {\left( { – 1} \right)^2}{.2^2} = 4;{t_3} = {\left( { – 1} \right)^3}{.3^2} = – 9$, suy ra ${t_1} < {t_2},{t_2} > {t_3}$. Vậy $\left( {{t_n}} \right)$ là dãy số không tăng không giảm.
a) Ta có: ${u_{n + 1}} = \frac{{2\left( {n + 1} \right) – 1}}{{\left( {n + 1} \right) + 1}} = \frac{{2n + 2 – 1}}{{n + 1 + 1}} = \frac{{2n + 1}}{{n + 2}}$
Xét hiệu:
$\begin{array}{l}{u_{n + 1}} – {u_n} = \frac{{2n + 1}}{{n + 2}} – \frac{{2n – 1}}{{n + 1}} = \frac{{\left( {2n + 1} \right)\left( {n + 1} \right) – \left( {2n – 1} \right)\left( {n + 2} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\ = \frac{{\left( {2{n^2} + n + 2n + 1} \right) – \left( {2{n^2} – n + 4n – 2} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\ = \frac{{2{n^2} + n + 2n + 1 – 2{n^2} + n – 4n + 2}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} = \frac{3}{{\left( {n + 2} \right)\left( {n + 1} \right)}} > 0,\forall n \in {\mathbb{N}^*}\end{array}$
Vậy ${u_{n + 1}} – {u_n} > 0 \Leftrightarrow {u_{n + 1}} > {u_n}$. Vậy dãy số $\left( {{u_n}} \right)$ là dãy số tăng.
b) Ta có: ${x_{n + 1}} = \frac{{\left( {n + 1} \right) + 2}}{{{4^{n + 1}}}} = \frac{{n + 1 + 2}}{{{{4.4}^n}}} = \frac{{n + 3}}{{{{4.4}^n}}}$
Xét hiệu:
${x_{n + 1}} – {x_n} = \frac{{n + 3}}{{{{4.4}^n}}} – \frac{{n + 2}}{{{4^n}}} = \frac{{n + 3 – 4\left( {n + 2} \right)}}{{{{4.4}^n}}} = \frac{{n + 3 – 4n – 8}}{{{{4.4}^n}}} = \frac{{ – 3n – 5}}{{{{4.4}^n}}} < 0,\forall n \in {\mathbb{N}^*}$
Vậy ${x_{n + 1}} – {x_n} < 0 \Leftrightarrow {x_{n + 1}} < {x_n}$. Vậy dãy số $\left( {{x_n}} \right)$ là dãy số giảm.
c) Ta có: ${t_1} = {\left( { – 1} \right)^1}{.1^2} = – 1;{t_2} = {\left( { – 1} \right)^2}{.2^2} = 4;{t_3} = {\left( { – 1} \right)^3}{.3^2} = – 9$, suy ra ${t_1} < {t_2},{t_2} > {t_3}$. Vậy $\left( {{t_n}} \right)$ là dãy số không tăng không giảm.
Giải Toán 11 tập 1 trang 49
Vận dụng 3 trang 49 Toán 11 tập 1
Một chồng cột gỗ được xếp thành các lớp, hai lớp liên tiếp hơn kém nhau 1 cột gỗ (Hình 2).
a) Gọi ${u_1} = 25$ là số cột gỗ có ở hàng dưới cùng của chồng cột gỗ, ${u_n}$ là số cột gỗ có ở hàng thứ $n$ tính từ dưới lên trên. Xét tính tăng, giảm của dãy số này.
b) Gọi ${v_1} = 14$ là số cột gỗ có ở hàng trên cùng của chồng cột gỗ, ${v_n}$ là số cột gỗ có ở hàng thứ $n$ tính từ trên xuống dưới. Xét tính tăng, giảm của dãy số này.
Lời giải:
a) Ta có:
$\begin{array}{l}{u_1} = 25\\{u_2} = 24 = {u_1} – 1\\{u_3} = 23 = {u_2} – 1\\ \vdots \end{array}$
Vậy công thức truy hồi: ${u_n} = {u_{n – 1}} – 1\left( {n \ge 2} \right) \Leftrightarrow {u_n} – {u_{n – 1}} = – 1 < 0$.
Vậy $\left( {{u_n}} \right)$ là dãy số giảm.
b) Ta có:
$\begin{array}{l}{v_1} = 14\\{v_2} = 15 = {v_1} + 1\\{v_3} = 16 = {v_2} + 1\\ \vdots \end{array}$
Vậy công thức truy hồi: ${v_n} = {v_{n – 1}} + 1\left( {n \ge 2} \right) \Leftrightarrow {v_n} – {v_{n – 1}} = 1 > 0$.
Vậy $\left( {{v_n}} \right)$ là dãy số tăng.
Hoạt động 5 trang 49 Toán 11 tập 1
Cho dãy số $\left( {{u_n}} \right)$ với ${u_n} = \frac{1}{n}$. So sánh các số hạng của dãy số với 0 và 1.
Lời giải:
$\forall n \in {\mathbb{N}^*}$ ta có:
$\left. \begin{array}{l}1 > 0\\n > 0\end{array} \right\} \Leftrightarrow \frac{1}{n} > 0 \Leftrightarrow {u_n} > 0$
$n \ge 1 \Leftrightarrow {u_n} = \frac{1}{n} \le \frac{1}{1} \Leftrightarrow {u_n} \le 1$
Thực hành 4 trang 49 Toán 11 tập 1
Xét tính bị chặn của các dãy số sau:
a) $\left( {{a_n}} \right)$ với ${a_n} = \cos \frac{\pi }{n}$;
b) $\left( {{b_n}} \right)$ với ${b_n} = \frac{n}{{n + 1}}$
Lời giải:
a) Ta có: $ – 1 \le \cos \frac{\pi }{n} \le 1,\forall n \in {\mathbb{N}^*} \Leftrightarrow – 1 \le {a_n} \le 1,\forall n \in {\mathbb{N}^*}$.
Vậy dãy số $\left( {{a_n}} \right)$ bị chặn.
b) $\forall n \in {\mathbb{N}^*}$ ta có:
$n > 0 \Leftrightarrow n + 1 > 0 \Leftrightarrow \frac{n}{{n + 1}} > 0 \Leftrightarrow {b_n} > 0$. Vậy $\left( {{b_n}} \right)$ bị chặn dưới.
${b_n} = \frac{n}{{n + 1}} = \frac{{\left( {n + 1} \right) – 1}}{{n + 1}} = 1 – \frac{1}{{n + 1}}$
Vì $n + 1 > 0 \Leftrightarrow \frac{1}{{n + 1}} > 0 \Leftrightarrow – \frac{1}{{n + 1}} < 0 \Leftrightarrow 1 – \frac{1}{{n + 1}} < 1 \Leftrightarrow {b_n} < 1$. Vậy $\left( {{b_n}} \right)$ bị chặn trên.
Ta thấy dãy số $\left( {{b_n}} \right)$ bị chặn trên và bị chặn dưới nên dãy số $\left( {{b_n}} \right)$ bị chặn.
Giải Toán 11 tập 1 trang 50
Giải bài 1 trang 50 Toán 11 tập 1
Tìm $u_{2}, u_{3}$ và dự đoán công thức số hạng tổng quát $u_{n}$ của dãy số:
$\left\{\begin{matrix}u_{1}=1\\u_{n+1}=\frac{u_{n}}{1+u_{n}} (n\geq 1)\end{matrix}\right.$
Lời giải
$u_{2}= \frac{1}{2}; u_{3}= \frac{1}{3}$
$u_{n}=\frac{1}{n}$
Giải bài 2 trang 50 Toán 11 tập 1
Cho dãy số $(u_{n}) với u_{n}=\frac{1}{1.2}+\frac{1}{2.3}+…+\frac{1}{n(n+1)}$. Tìm $u_{1}, u_{2}, u_{3}$ và dự đoán công thức số hạng tổng quát $u_{n}$
Lời giải
$u_{1}= \frac{1}{2}; u_{2}=\frac{2}{3}; u_{3} = \frac{3}{4}$
$u_{n}= \frac{n}{n+1}$
Giải bài 3 trang 50 Toán 11 tập 1
Xét tính tăng, giảm của dãy số $(y_{n}) với y_{n}=\sqrt{n+1}-\sqrt{n}$
Lời giải
Ta có:
$y_{n} = \sqrt{n+1}-\sqrt{n} = \frac{(\sqrt{n+1}-\sqrt{n}).(\sqrt{n+1}+\sqrt{n})}{\sqrt{n+1}+\sqrt{n}} = \frac{1}{\sqrt{n+1}+\sqrt{n}}$
$y_{n+1} = \frac{1}{\sqrt{n+2}+\sqrt{n+1}}$
$\forall n \in N* , y_{n+1} < y_{n}$
Vậy dãy số $(y_{n})$ là dãy số giảm
Giải bài 4 trang 50 Toán 11 tập 1
Xét tính bị chặn của các dãy số sau:
a) $(a_{n}) với a_{n}=sin^{2}\frac{n\pi }{3}+cos\frac{n\pi }{4}$
b) $(u_{n}) với u_{n}=\frac{6n-4}{n+2}$
Lời giải
a) $\forall n\in \mathbb{N}^{*}$, Ta có:
$0\leq sin^{2}\frac{n\pi }{3} \leq 1$
$-1\leq cos\frac{n\pi }{4} \leq 1$
Suy ra $- 1\leq a_{n} \leq 2$
Vậy dãy số $(a_{n})$ bị chặn
b) $u_{n}=\frac{6n-4}{n+2} = 6 -\frac{16}{n+2}$
$u_{n} < 6, \forall n\in \mathbb{N}^{*}$. Vậy dãy số $(u_{n})$ bị chặn trên
$u_{n} >-2, \forall n\in \mathbb{N}^{*}$. Vậy dãy số $(u_{n})$ bị chặn dưới
Suy ra, dãy số $(u_{n})$ bị chặn
Giải bài 5 trang 50 Toán 11 tập 1
Cho dãy số $(u_{n}) với u_{n}=\frac{2n-1}{n+1}$
Chứng minh $(u_{n})$ là dãy số tăng và bị chặn
Lời giải
$u_{n}=\frac{2n-1}{n+1} = 2 – \frac{3}{n+1}$
Ta có $\forall n\in \mathbb{N}^{*}, u_{n+1}=2 – \frac{3}{n+2}> u_{n} = 2 – \frac{3}{n+1}$
Vậy dãy số $(u_{n})$ là dãy số tăng
$u_{n}= 2 – \frac{3}{n+1} > -1, \forall n\in \mathbb{N}^{*}$. Vậy dãy số $(u_{n})$ bị chặn dưới
$u_{n}= 2 – \frac{3}{n+1} < 2, \forall n\in \mathbb{N}^{*}$. Vậy dãy số $(u_{n})$ bị chặn trên
Suy ra dãy số $(u_{n})$ bị chặn
Giải bài 6 trang 50 Toán 11 tập 1
Cho dãy số $(u_{n}) với u_{n}=\frac{na+2}{n+1}$. Tìm giá trị của a để:
a) $(u_{n})$ là dãy số tăng
b) $(u_{n})$ là dãy số giảm
Lời giải
a) $(u_{n})$ là dãy số tăng khi $\forall x \in \mathbb{N}^{*} thì: u_{n+1}>u_{n}$
$\Leftrightarrow \frac{(n+1)a+2}{n+1+1}>\frac{na+2}{n+1}; \forall x \in \mathbb{N}^{*}$
$\Leftrightarrow a+\frac{2-a}{n+2}>a+\frac{2-a}{n+1}; \forall x \in \mathbb{N}^{*}$
$\Leftrightarrow \frac{2-a}{n+2}>\frac{2-a}{n+1}; \forall x \in \mathbb{N}^{*}$
$\Leftrightarrow 2-a <0$
$\Leftrightarrow a>2$
b) $(u_{n})$ là dãy số tăng khi $\forall x \in \mathbb{N}^{*}$ thì: $u_{n+1} < u_{n}$
$\Leftrightarrow \frac{(n+1)a+2}{n+1+1}<\frac{na+2}{n+1}; \forall x \in \mathbb{N}^{*}$
$\Leftrightarrow a+\frac{2-a}{n+2}< a+\frac{2-a}{n+1}; \forall x \in \mathbb{N}^{*}$
$\Leftrightarrow \frac{2-a}{n+2}<\frac{2-a}{n+1}; \forall x \in \mathbb{N}^{*}$
$\Leftrightarrow 2-a >0$
$\Leftrightarrow a<2$
Giải bài 7 trang 50 Toán 11 tập 1
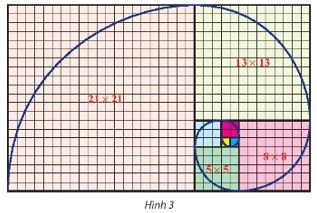
Trên lưới ô vuông, mỗi ô cạnh 1 đơn vị, người ta vẽ 8 hình vuông và tô màu khác nhau như Hình 3. Tìm dãy số biểu diễn độ dài cạnh của 8 hình vuông đó từ nhỏ đến lớn. Có nhận xét gì về dãy số trên?
Lời giải
$u_{1}=1; u_{2}=1; u_{3}=2; u_{4}=3; u_{5}=5; u_{6}=8; u_{7}=13; u_{8}=21$
Ta có dãy số $(u_{n}) : \left\{\begin{matrix}u_{1}=1\\ u_{2}=1\\u_{n} = u_{n-1}+u_{n-2}\end{matrix}\right.$

Lời giải:
a) Ta có:
$\begin{array}{l}{u_1} = 25\\{u_2} = 24 = {u_1} – 1\\{u_3} = 23 = {u_2} – 1\\ \vdots \end{array}$
Vậy công thức truy hồi: ${u_n} = {u_{n – 1}} – 1\left( {n \ge 2} \right) \Leftrightarrow {u_n} – {u_{n – 1}} = – 1 < 0$.
Vậy $\left( {{u_n}} \right)$ là dãy số giảm.
b) Ta có:
$\begin{array}{l}{v_1} = 14\\{v_2} = 15 = {v_1} + 1\\{v_3} = 16 = {v_2} + 1\\ \vdots \end{array}$
Vậy công thức truy hồi: ${v_n} = {v_{n – 1}} + 1\left( {n \ge 2} \right) \Leftrightarrow {v_n} – {v_{n – 1}} = 1 > 0$.
Vậy $\left( {{v_n}} \right)$ là dãy số tăng.
