Giải toán 11 tập 2 trang 81 bài 4: Khoảng cách trong không gian
Giải toán 11 tập 2 trang 81 bài 4: Khoảng cách trong không gian
Giải toán 11 tập 2 trang 81 Bài 4 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 11 Chân trời sáng tạo. Mời các em học sinh cùng quý phụ huynh tham khảo.
Giải toán 11 tập 2 trang 74
Hoạt động 1 trang 74 toán 11 tập 2
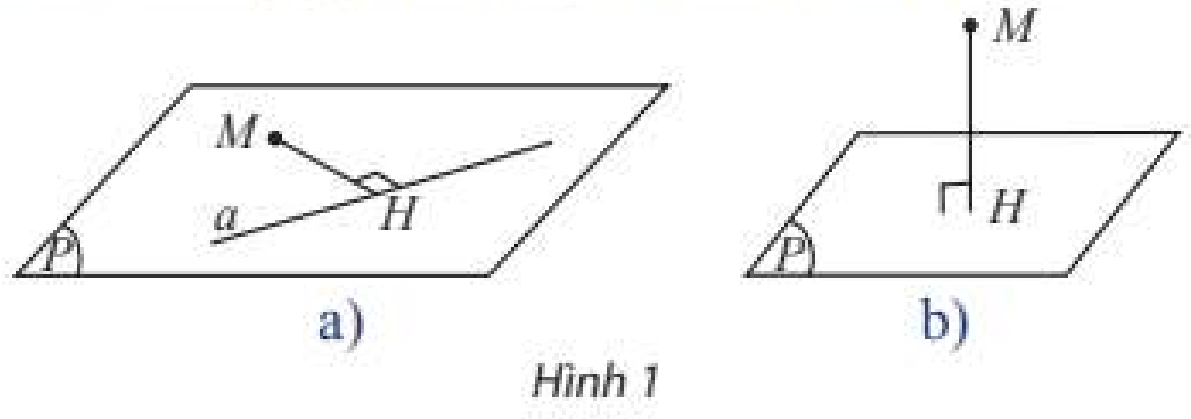
a) Cho điểm $M$ và đường thẳng $a$ không đi qua $M$. Trong mặt phẳng $\left( {M,a} \right)$, dùng êke để tìm điểm $H$ trên $a$ sao cho $MH \bot a$ (Hình 1a). Đo độ dài đoạn $MH$.
b) Cho điểm $M$ không nằm trên mặt phẳng sàn nhà $\left( P \right)$. Dùng dây dọi để tìm hình chiếu vuông góc $H$ của $M$ trên $\left( P \right)$ (Hình 1b). Đo độ dài đoạn $MH$.
Giải toán 11 tập 2 trang 75
Thực hành 1 trang 75 toán 11 tập 2
Cho hình chóp $S.ABCD$ với đáy $ABCD$ là hình vuông cạnh $a$. Cho biết $SA = a$ và $SA$ vuông góc với $\left( {ABCD} \right)$.
a) Tính khoảng cách từ điểm $B$ đến $\left( {SAD} \right)$.
b) Tính khoảng cách từ điểm $A$ đến cạnh $SC$.
Lời giải:

a) Ta có:
$\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB\\AB \bot A{\rm{D}}\end{array} \right\} \Rightarrow AB \bot \left( {SA{\rm{D}}} \right)\\ \Rightarrow d\left( {B,\left( {SA{\rm{D}}} \right)} \right) = AB = a\end{array}$
b) Kẻ $AH \bot SC \Rightarrow d\left( {A,SC} \right) = AH$
Tam giác $ABC$ vuông tại $B$$ \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 $
Tam giác $SAC$ vuông tại $A$$ \Rightarrow SC = \sqrt {S{A^2} + A{C^2}} = a\sqrt 3 $
Tam giác $SAC$ vuông tại $A$ có đường cao $AH$$ \Rightarrow AH = \frac{{SA.AC}}{{SC}} = \frac{{a\sqrt 6 }}{3}$
Vậy $d\left( {A,SC} \right) = \frac{{a\sqrt 6 }}{3}$.
Vận dụng 1 trang 75 toán 11 tập 2
Một quạt trần có bề dày của thân quạt là 20 cm. Người muốn treo quạt sao cho khoảng cách từ đỉnh quạt đến sàn nhà là 2,5 m. Hỏi phải làm cán quạt dài bao nhiêu? Cho biết trần nhà cao 3,6 m
Lời giải:
Đổi $20cm = 0,2m$
Độ dài của cán quạt là: $3,6 – 2,5 – 0,2 = 0,9\left( m \right)$.
Giải toán 11 tập 2 trang 76
Hoạt động 2 trang 76 toán 11 tập 2
a) Cho đường thẳng $a$ song song với mặt phẳng $\left( P \right)$. Lấy hai điểm $A,B$ tuỳ ý trên $a$ và gọi $H,K$ lần lượt là hình chiếu vuông góc của $A$ và $B$ trên $\left( P \right)$ (Hình 4a). So sánh độ dài hai đoạn thẳng $AH$ và $BK$.
b) Cho hai mặt phẳng song song $\left( P \right)$ và $\left( Q \right)$. Lấy hai điểm $A,B$ tuỳ ý trên $\left( P \right)$ và gọi $H,K$ lần lượt là hình chiếu vuông góc của $A$ và $B$ trên $\left( Q \right)$ (Hình 4b). So sánh độ dài hai đoạn thẳng $AH$ và $BK$.

Lời giải:
a) Ta có:
$\left. \begin{array}{l}AH \bot \left( P \right)\\BK \bot \left( P \right)\end{array} \right\} \Rightarrow AH\parallel BK$
Mà $AB\parallel HK$
$ \Rightarrow ABKH$ là hình bình hành có $AH \bot \left( P \right) \Rightarrow AH \bot HK \Rightarrow \widehat {AHK} = {90^ \circ }$
Vậy $ABKH$ là hình chữ nhật.
Vậy $AH = BK$.
b) Ta có:
$\left. \begin{array}{l}AH \bot \left( Q \right)\\BK \bot \left( Q \right)\end{array} \right\} \Rightarrow AH\parallel BK$
Mà $AB\parallel HK$
$ \Rightarrow ABKH$ là hình bình hành có $AH \bot \left( Q \right) \Rightarrow AH \bot HK \Rightarrow \widehat {AHK} = {90^ \circ }$
Vậy $ABKH$ là hình chữ nhật.
Vậy $AH = BK$.
Giải toán 11 tập 2 trang 77
Thực hành 2 trang 77 toán 11 tập 2
Cho hình lập phương $ABCD.A’B’C’D’$ có cạnh bằng $a$. Tính khoảng cách:
a) Giữa hai mặt phẳng $\left( {ACD’} \right)$ và $\left( {A’C’B} \right)$.
b) Giữa đường thẳng $AB$ và $\left( {A’B’C’D’} \right)$.
Lời giải:

a) $AA’C’C$ là hình chữ nhật
$\left. \begin{array}{l} \Rightarrow AC\parallel A’C’\\A’C’ \subset \left( {A’C’B} \right)\end{array} \right\} \Rightarrow AC\parallel \left( {A’C’B} \right)$
$ABC’D’$ là hình bình hành
$\left. \begin{array}{l} \Rightarrow AD’\parallel BC’\\BC’ \subset \left( {A’C’B} \right)\end{array} \right\} \Rightarrow AD’\parallel \left( {A’C’B} \right)$
Ta có:
$\left. \begin{array}{l}AC\parallel \left( {A’C’B} \right)\\AD’\parallel \left( {A’C’B} \right)\\AC,A{\rm{D}}’ \subset \left( {AC{\rm{D}}’} \right)\end{array} \right\} \Rightarrow \left( {AC{\rm{D}}’} \right)\parallel \left( {A’C’B} \right) \Rightarrow \left( {\left( {AC{\rm{D}}’} \right),\left( {A’C’B} \right)} \right) = {0^ \circ }$
b) Ta có:
$\left. \begin{array}{l}AB\parallel A’B’\\A’B’ \subset \left( {A’B’C’D’} \right)\end{array} \right\} \Rightarrow AB\parallel \left( {A’B’C’D’} \right) \Rightarrow \left( {AB,\left( {A’B’C’D’} \right)} \right) = {0^ \circ }$
Hoạt động 3 trang 77 toán 11 tập 2
Cho hai đường thẳng chéo nhau $a$ và $b$. Gọi $\left( Q \right)$ là mặt phẳng chứa $b$ và song song với $a$. Gọi $\left( P \right)$ là mặt phẳng chứa đường thẳng $a$, vuông góc với $\left( Q \right)$ và cắt $b$ tại điểm $J$. Trong $\left( P \right)$, gọi $c$ là đường thẳng đi qua $J$, vuông góc với $a$ và cắt $a$ tại điểm $I$.
Đường thẳng $IJ$ có vuông góc với $b$ không? Giải thích.

Lời giải:
Gọi $\left( R \right)$ là mặt phẳng chứa $a$và song song với $\left( Q \right)$. Ta có:
$\left. \begin{array}{l}\left( Q \right)\parallel \left( R \right)\\\left( P \right) \cap \left( Q \right) = a’\\\left( P \right) \cap \left( R \right) = a\end{array} \right\} \Rightarrow a\parallel a’$
Mà $IJ \bot a \Rightarrow IJ \bot a’$
$\left. \begin{array}{l}\left( P \right) \bot \left( Q \right)\\\left( P \right) \cap \left( Q \right) = a’\\IJ \subset \left( P \right),IJ \bot a’\end{array} \right\} \Rightarrow IJ \bot \left( Q \right)$
Mà $b \subset \left( Q \right) \Rightarrow IJ \bot b$.
Giải toán 11 tập 2 trang 78
Thực hành 3 trang 78 toán 11 tập 2
Cho tứ diện $OABC$ có ba cạnh $OA,OB,OC$ đều bằng $a$ và vuông góc từng đôi một. Tính khoảng cách giữa hai đường thẳng:
a) $OA$ và $BC$;
b) $OB$ và $AC$.
Lời giải:

a) Gọi $M$ là trung điểm của $BC$.
Tam giác $OBC$ vuông cân tại $O \Rightarrow OM \bot BC$
$\left. \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OA \bot \left( {OBC} \right) \Rightarrow OA \bot OM$
$ \Rightarrow d\left( {OA,BC} \right) = OM = \frac{1}{2}BC = \frac{1}{2}\sqrt {O{B^2} + O{C^2}} = \frac{{a\sqrt 2 }}{2}$
b) Gọi $N$ là trung điểm của $AC$.
Tam giác $OAC$ vuông cân tại $O \Rightarrow ON \bot AC$
$\left. \begin{array}{l}OA \bot OB\\OB \bot OC\end{array} \right\} \Rightarrow OB \bot \left( {OAC} \right) \Rightarrow OB \bot ON$
$ \Rightarrow d\left( {OB,AC} \right) = ON = \frac{1}{2}AC = \frac{1}{2}\sqrt {O{A^2} + O{C^2}} = \frac{{a\sqrt 2 }}{2}$
Vận dụng 2 trang 78 toán 11 tập 2
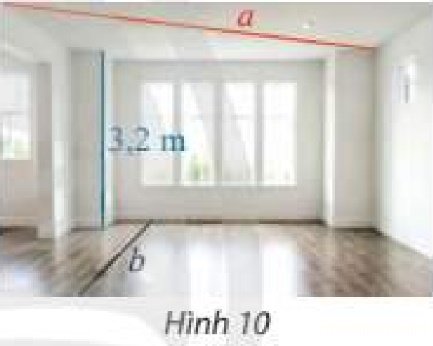
Một căn phòng có trần cao 3,2 m. Tỉnh khoảng cách giữa một đường thẳng $a$ trên trần nhà và đường thẳng $b$ trên sàn nhà.
Lời giải:
Vì trần nhà và sàn nhà song song với nhau nên đường thẳng $a$ nằm trên trần nhà song song với sàn nhà.
Vậy khoảng cách giữa đường thẳng $a$ trên trần nhà và đường thẳng $b$ trên sàn nhà bằng khoảng cách giữa trần nhà và sàn nhà. Khoảng cách đó bằng 3,2 m.
Hoạt động 4 trang 78 toán 11 tập 2
Cho một khối hộp chữ nhật với các kích thước là $a,b,c$ đều là số nguyên dương. Về các mặt phẳng song song với các mặt của hình hộp và chia nó thành các khối lập phương có cạnh bằng 1 (Hình 11). Tìm số hình lập phương đơn vị có trong hình hộp.

Lời giải:
Số hình lập phương đơn vị có trong hình hộp là: $abc$.
Giải toán 11 tập 2 trang 79
Hoạt động 5 trang 79 toán 11 tập 2
Cho khối lăng trụ tam giác $ABC.A’B’C’$ (Hình 14). Tìm cách chia khối lăng trụ thành ba khối chóp có cùng chiều cao và diện tích đáy.

Lời giải:
Chia khối lăng trụ tam giác $ABC.A’B’C’$ thành ba khối chóp: $A.A’B’C’,B’.ABC$ và $C.A’B’C’$.
Giải toán 11 tập 2 trang 81
Thực hành 4 trang 81 toán 11 tập 2
Tính thể tích của một bồn chứa có dạng khối chóp cụt đều có kích thước được cho như trong Hình 20.

Lời giải:
Diện tích đáy lớn là: $S = {5^2} = 25\left( {{m^2}} \right)$
Diện tích đáy bé là: $S’ = {2^2} = 4\left( {{m^2}} \right)$
Thể tích của bồn chứa là: $V = \frac{1}{3}.3\left( {25 + \sqrt {25.4} + 4} \right) = 39\left( {{m^3}} \right)$
Vận dụng 3 trang 81 toán 11 tập 2
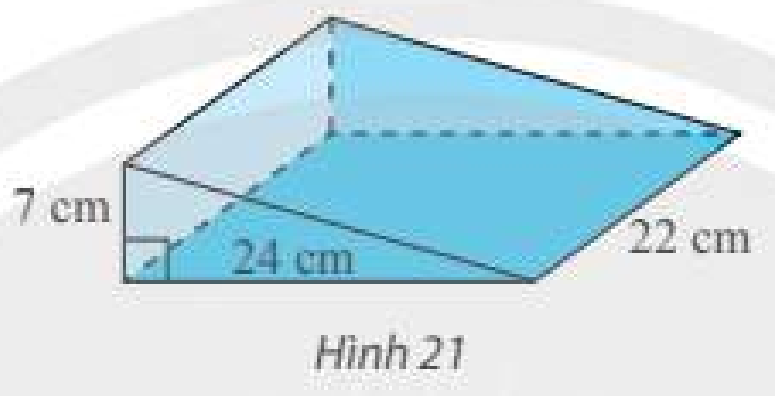
Tính thể tích cái nêm hình lăng trụ đứng có kích thước như trong Hình 21.
Lời giải:
Diện tích đáy của lăng trụ là: $\frac{1}{2}.7.24 = 84\left( {c{m^2}} \right)$
Thể tích cái nêm hình lăng trụ đứng là: $84.22 = 1848\left( {c{m^3}} \right)$
Giải bài 1 trang 81 Toán 11 tập 2
Cho hình chóp S.ABCD, đáy ABCD là hình thoi cạnh a có O là giao điểm của hai đường chéo, $\widehat{ABC} = 60^{o}, SO\perp (ABCD), SO = a\sqrt{3}$. Tính khoảng cách từ O đến mặt phẳng (SCD)
Bài làm
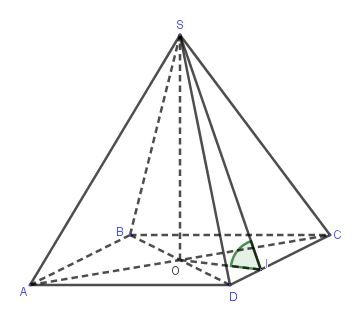
Kẻ OI $\perp$ CD; OH $\perp$ SI
SO $\perp$ (ABCD) nên SO $\perp$ CD
Ta có: CD $\perp$ SO, CD $\perp$ OI nên CD $\perp$ (SOI) . Suy ra CD $\perp$ OH
Mà OH $\perp$ SI nên OH $\perp$ (SCD)
Ta có ABCD là hình thoi cạnh a, $\widehat{ABC} = 60^{o} nên AC = a, OC = \frac{a}{2}, \widehat{ACD} = 60^{o}$
$OI = \frac{a}{2}.sin60^{o} = \frac{a\sqrt{3}}{4}$
Tam giác SOI vuông tại O có đường cao OH: $\frac{1}{OH^{2}}=\frac{1}{OI^{2}}+\frac{1}{SO^{2}} Suy ra OH = \frac{a\sqrt{51}}{17}$
$d(SO,(SCD)) = d(O,(SCD))= OH = \frac{a\sqrt{51}}{17}$
Giải bài 2 trang 81 Toán 11 tập 2
Cho hai tam giác cân ABC và ABD có đáy chung AB và không cùng nằm trong một mặt phẳng.
a) Chứng minh rằng AB ⊥ CD
b) Xác định đoạn vuông góc chung của AB và CD
Bài làm
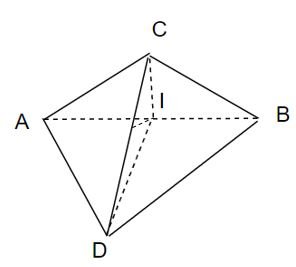
a) Gọi I là trung điểm AB.
Tam giác ABC cân tại C có I là trung điểm nên CI ⊥ AB
Tam giác ABD cân tại D có I là trung điểm nên DI ⊥ AB
Suy ra AB ⊥ (CID)
Nên AB ⊥ CD
b) Kẻ IH ⊥ CD
Mà AB ⊥ (CID) nên AB ⊥ IH
Vậy đoạn vuông góc chung giữa AB và CD là IH
Giải bài 3 trang 81 Toán 11 tập 2
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA = SB = SC = SD = $a\sqrt{2}$. Gọi I, J lần lượt là trung điểm của AB và CD
a) Chứng minh AB ⊥ (SIJ)
b) Tính khoảng cách giữa hai đường thẳng AB và SC
Bài làm
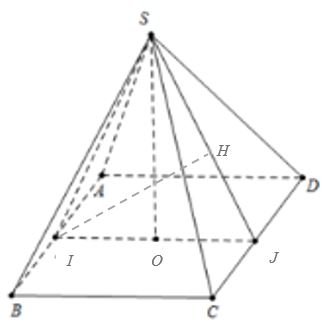
a) S.ABCD là hình chóp đều, O là tâm của đáy nên SO ⊥ (ABCD)
Nên SO ⊥ AB
Mà I, J lần lượt là trung điểm của AB và CD nên IJ ⊥ AB
Suy ra: AB ⊥ (SIJ)
b) Kẻ IH ⊥ SJ
Vì AB ⊥ (SIJ) nên AB ⊥ IH
Ta có: SO ⊥ (ABCD) nên SO ⊥ CD. Mà CD ⊥ IJ nên CD ⊥ SIJ)
Suy ra: CD ⊥ IH. Mà IH ⊥ SJ nên IH ⊥ (SCD) và IH ⊥ CD
Ta có: SJ = $\sqrt{SC^{2}-CJ^{2}}=\frac{a\sqrt{7}}{2}$
SO = $\sqrt{SC^{2}-OC^{2}} = \frac{a\sqrt{6}}{2}$
$S_{SIJ} = \frac{1}{2}.IH.SJ=\frac{1}{2}.SO.IJ . Suy ra: IH=\frac{a\sqrt{42}}{7}$
$d(AB,SC) = IH = \frac{a\sqrt{42}}{7}$
Giải bài 4 trang 81 Toán 11 tập 2
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có AB = a, góc giữa hai mrụặt phẳng (A’BC) và (ABC) bằng 60o.
a) Tính khoảng cách giữa hai đáy của hình lăng trụ
b) Tính thể tích của khối lăng trụ
Bài làm

a) Gọi M là trung điểm của BC. Tam giác ABC đều nên AM⊥BC
Mà BC ⊥ AA′ nên BC ⊥ (AA′M). Suy ra BC ⊥ A′M
Mặt khác (ABC) ∩ (A′BC) = BC
Nên ((ABC);(A’BC)) = $\widehat{A’MA} = 60^{o}$
Tam giác ABC đều cạnh a nên AM = $\frac{a\sqrt{3}}{2}$
$AA’=AM.tan60^{o} = \frac{3a}{2}$
b) $S_{ABC} = \frac{a^{2}\sqrt{3}}{4}$
$V_{ABC.A’B’C’} = \frac{3a}{2}.\frac{a^{2}\sqrt{3}}{4} = \frac{3a^{3}\sqrt{3}}{8}$
Giải bài 5 trang 81 Toán 11 tập 2
Một cây cầu dành cho người đi bộ (Hình 22) có mặt sàn cầu cách mặt đường 3,5 m, khoảng cách từ đường thẳng a nằm trên tay vịn của cầu đến mặt sàn cầu là 0,8 m. Gọi b là đường thẳng kẻ theo tim đường. Tính khoảng cách giữa hai đường thẳng a và b

Bài làm
Vì tay vịn cầu song song với mặt đường nên khoảng cách giữa hai đường thẳng $a$ và $b$ chính bằng khoảng cách từ đường thẳng $a$ xuống mặt đường.
Khoảng cách giữa hai đường thẳng $a$ và $b$ bằng: $3,5 + 0,8 = 4,3\left( m \right)$.
Giải toán 11 tập 2 trang 82
Giải bài 6 trang 82 Toán 11 tập 2
Cho hình hộp đứng ABCD.A’B’C’D’ có cạnh bên AA’ = 2a và đáy ABCD là hình thoi có AB = a và AC = $a\sqrt{3}$
a) Tính khoảng cách giữa hai đường thẳng BD và AA’
b) Tính thể tích của khối hộp
Bài làm
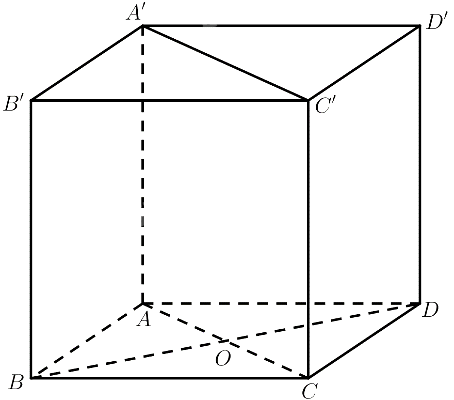
a) Gọi $O = AC \cap B{\rm{D}}$
$ABCD$ là hình thoi $ \Rightarrow AC \bot B{\rm{D}} \Rightarrow AO \bot B{\rm{D}}$
$AA’ \bot \left( {ABCD} \right) \Rightarrow AA’ \bot AO$
$ \Rightarrow d\left( {B{\rm{D}},AA’} \right) = AO = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}$
b) Tam giác $OAB$ vuông tại $O$
$\begin{array}{l} \Rightarrow BO = \sqrt {A{B^2} – A{O^2}} = \frac{a}{2} \Rightarrow B{\rm{D}} = 2BO = a\\{S_{ABC{\rm{D}}}} = \frac{1}{2}AC.B{\rm{D}} = \frac{{{a^2}\sqrt 3 }}{2}\\{V_{ABC.A’B’C’}} = {S_{ABC{\rm{D}}}}.AA’ = \frac{{3{a^3}}}{4}\end{array}$
Giải bài 7 trang 82 Toán 11 tập 2
Cho khối chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a và có O là giao điểm hai đường chéo của đáy.
a) Tính khoảng cách giữa hai đường thẳng AC và SB
b) Tính thể tích của khối chóp
Lời giải
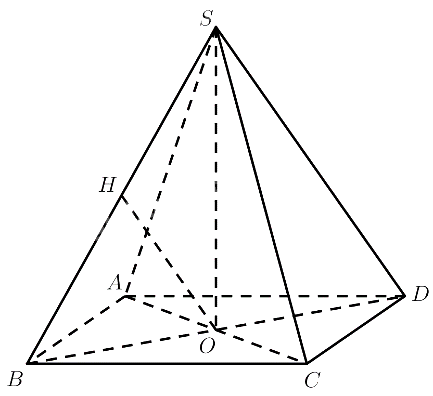
a) Kẻ $OH \bot SB\left( {H \in SB} \right)$
$S.ABC{\rm{D}}$ là chóp tứ giác đều $ \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AC$
$ABC{\rm{D}}$ là hình vuông $ \Rightarrow AC \bot B{\rm{D}}$
$ \Rightarrow AC \bot \left( {SB{\rm{D}}} \right) \Rightarrow AC \bot OH$
Mà $OH \bot SB$
$ \Rightarrow d\left( {AC,SB} \right) = OH$
$B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2}} = a\sqrt 2 \Rightarrow BO = \frac{1}{2}B{\rm{D}} = \frac{{a\sqrt 2 }}{2}$
$\Delta SBO$ vuông tại $O \Rightarrow SO = \sqrt {S{B^2} – B{O^2}} = \frac{{a\sqrt 2 }}{2}$
$\Delta SBO$ vuông cân tại $O$ có đường cao $OH$
$ \Rightarrow d\left( {AC,SB} \right) = OH = \frac{1}{2}SB = \frac{a}{2}$
b) ${S_{ABC{\rm{D}}}} = A{B^2} = {a^2}$
${V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SO = \frac{{{a^3}\sqrt 2 }}{6}$
Giải bài 8 trang 82 Toán 11 tập 2
Tính thể tích của khối chóp cụt lục giác đều ABCDEF.A’B’C’D’E’F’ với O và O’ là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là a và $\frac{a}{2}$, OO’ = a
Lời giải

Diện tích đáy lớn là: $S = 6{S_{ABO}} = 6.\frac{{A{B^2}\sqrt 3 }}{4} = \frac{{3{a^2}\sqrt 3 }}{2}$
Diện tích đáy bé là: $S’ = 6{S_{A’B’O’}} = 6.\frac{{A’B{‘^2}\sqrt 3 }}{4} = \frac{{3{a^2}\sqrt 3 }}{8}$
Thể tích khối chóp cụt lục giác đều là:
$V = \frac{1}{3}.a\left( {\frac{{3{a^2}\sqrt 3 }}{2} + \sqrt {\frac{{3{a^2}\sqrt 3 }}{2}.\frac{{3{a^2}\sqrt 3 }}{8}} + \frac{{3{a^2}\sqrt 3 }}{8}} \right) = \frac{{3{a^3}\sqrt 3 }}{8}$
