Toán 11 tập 1 trang 40 Bài 4: Phương trình lượng giác cơ bản
Toán 11 tập 1 trang 40 Bài 4: Phương trình lượng giác cơ bản
Giải toán 11 tập 1 trang 40 Bài 4 sách Cánh diều có đáp án chi tiết cho từng Bài trong sách giáo khoa Toán lớp 11 Cánh diều. Mời các em học sinh cùng quý phụ huynh tham khảo.
Trang 32 toán 11 tập 1
HĐ 1 trang 32 toán 11 tập 1
Cho hai phương trình (với cùng ẩn x): ${x^2} – 3x + 2 = 0\,\,\,\left( 1 \right)$và $\left( {x – 1} \right)\left( {x – 2} \right) = 0\,\,\,\left( 2 \right)$
a) Tìm tập nghiệm ${S_1}$ của phương trình (1) và tập nghiệm ${S_2}$ của phương trình (2)
b) Hai tập ${S_1},{S_2}$ có bằng nhau hay không?
Lời giải:
a) Phương trình: ${x^2} – 3x + 2 = 0\,\,\,\left( 1 \right)$
Ta có: $\Delta = 9 – 4.2 = 1 > 0$
Phương trình (1) có hai nghiệm $\left\{ \begin{array}{l}{x_1} = \frac{{3 + 1}}{{2.1}} = 2\\{x_1} = \frac{{3 – 1}}{{2.1}} = 1\end{array} \right.$ => ${S_1} = \left\{ {1;2} \right\}$
Phương trình: $\left( {x – 1} \right)\left( {x – 2} \right) = 0\,\,\,\left( 2 \right)$$ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.$ => ${S_2} = \left\{ {1;2} \right\}$
b) Hai tập ${S_1};{S_2}$ có bằng nhau
LT – VD 1 trang 32 toán 11 tập 1
Hai phương trình $x – 1 = 0$ và $\frac{{{x^2} – 1}}{{x + 1}}$ có tương đương không vì sao?
Lời giải:
Hai phương trình $x – 1 = 0$và $\frac{{{x^2} – 1}}{{x + 1}} = 0$ có tương đương vì:
$\begin{array}{l}\frac{{{x^2} – 1}}{{x + 1}} = 0\\ \Leftrightarrow \frac{{\left( {x – 1} \right).\left( {x + 1} \right)}}{{x + 1}} = 0\\ \Leftrightarrow x – 1 = 0\end{array}$
Trang 33 toán 11 tập 1
HĐ 2 trang 33 toán 11 tập 1
Khẳng định $3x – 6 = 0 \Leftrightarrow 3x = 6$ đúng hay sai?
Lời giải:
Khẳng định $3x – 6 = 0 \Leftrightarrow 3x = 6$ đúng
LT – VD 2 trang 33 toán 11 tập 1
Giải phương trình: ${\left( {x – 1} \right)^2} = 5x – 11$
Lời giải:
$\begin{array}{l}{\left( {x – 1} \right)^2} = 5x – 11\\ \Leftrightarrow {x^2} – 2x + 1 = 5x – 11\\ \Leftrightarrow {x^2} – 2x + 1 – 5x + 11 = 0\\ \Leftrightarrow {x^2} – 7x – 10 = 0\\ \Leftrightarrow (x – 5)(x – 2) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 5\\x = 2\end{array} \right.\end{array}$
HĐ 3 trang 33 toán 11 tập 1
a) Đường thẳng $d:y = \frac{1}{2}$ cắt đồ thị hàm số $y = \sin x,x \in \left[ { – \pi ;\pi } \right]$ tại hai giao điểm ${A_0},{B_0}$ (Hình 34). Tìm hoành độ của hai giao điểm ${A_0},{B_0}$.
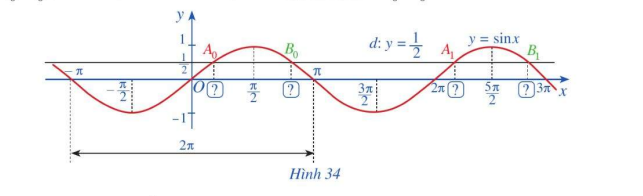
b) Đường thẳng $d:y = \frac{1}{2}$ cắt đồ thị hàm số $y = \sin x,x \in \left[ {\pi ;3\pi } \right]$ tại hai giao điểm ${A_1},{B_1}$ (Hình 34). Tìm hoành độ của hai giao điểm ${A_1},{B_1}$.
Lời giải:
a) Hoành độ của ${A_0}$ là $\frac{\pi }{6}$
Hoành độ của ${B_0}$ là $\frac{{5\pi }}{6}$
b) Hoành độ của ${A_1}$ là $\frac{{13\pi }}{6}$
Hoành độ của ${B_1}$ là $\frac{{17\pi }}{6}$
Trang 34 toán 11 tập 1
LT – VD 3 trang 34 toán 11 tập 1
a) Giải phương trình: $\sin x = \frac{{\sqrt 3 }}{2}$
b) Tìm góc lượng giác x sao cho $\sin x = \sin {55^ \circ }$
Lời giải:
a) $\sin x = \frac{{\sqrt 3 }}{2} \Leftrightarrow \sin x = \sin \frac{\pi }{3} \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = \pi – \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k2\pi \\x = \frac{{2\pi }}{3} + k2\pi \end{array} \right.$
b)
$\begin{array}{l}\sin x = \sin {55^ \circ } \Leftrightarrow \left[ \begin{array}{l}x = {55^ \circ } + k{.360^ \circ }\\x = {180^ \circ } – {55^ \circ } + k{.360^ \circ }\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = {55^ \circ } + k{.360^ \circ }\\x = {125^ \circ } + k{.360^ \circ }\end{array} \right.\\\end{array}$
Trang 35 toán 11 tập 1
LT – VD 4 trang 35 toán 11 tập 1
Giải phương trình $\sin 2x = \sin \left( {x + \frac{\pi }{4}} \right)$
Lời giải:
$\sin 2x = \sin \left( {x + \frac{\pi }{4}} \right) \Leftrightarrow \left[ \begin{array}{l}2x = x + \frac{\pi }{4} + k2\pi \\2x = \pi – \left( {x + \frac{\pi }{4}} \right) + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{4} + k2\pi \\3x = \frac{{3\pi }}{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{4} + k2\pi \\x = \frac{\pi }{4} + \frac{{k2\pi }}{3}\end{array} \right.$
HĐ 4 trang 35 toán 11 tập 1
a) Đường thẳng $d:y = \frac{1}{2}$ cắt đồ thị hàm số $y = \cos x,x \in \left[ { – \pi ;\pi } \right]$ tại hai giao điểm ${C_0},{D_0}$ (Hình 35). Tìm hoành độ giao điểm của hai giao điểm ${C_0},{D_0}$.
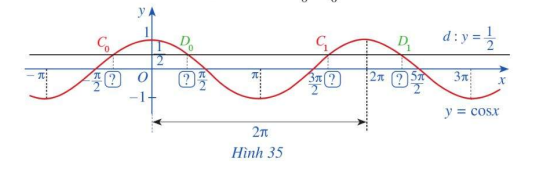
b) Đường thẳng $d:y = \frac{1}{2}$ cắt đồ thị hàm số $y = \cos x,x \in \left[ {\pi ;3\pi } \right]$ tại hai giao điểm ${C_1},{D_1}$ (Hình 35). Tìm hoành độ giao điểm của hai giao điểm ${C_1},{D_1}$.
Lời giải:
a) Hoành độ của ${C_0}$ là $ – \frac{\pi }{3}$
Hoành độ của ${D_0}$ là $\frac{\pi }{3}$
b) Hoành độ của ${C_1}$ là $\frac{{5\pi }}{3}$
Hoành độ của ${D_1}$ là $\frac{{7\pi }}{3}$
Trang 36 toán 11 tập 1
LT – VD 5 trang 36 toán 11 tập 1
a) Giải phương trình $\cos x = – \frac{1}{2}$
b) Tìm góc lượng giác x sao cho $\cos x = \cos \left( { – {{87}^ \circ }} \right)$
Lời giải:
a) $\cos x = – \frac{1}{2} \Leftrightarrow \cos x = \cos \left( {\frac{{2\pi }}{3}} \right) \Leftrightarrow \left[ \begin{array}{l}x = \frac{{2\pi }}{3} + k2\pi \\x = – \frac{{2\pi }}{3} + k2\pi \end{array} \right.$
b) $\cos x = \cos \left( { – {{87}^ \circ }} \right) \Leftrightarrow \left[ \begin{array}{l}x = – {87^ \circ } + k.360\\x = {87^ \circ } + k{.360^ \circ }\end{array} \right.$
Trang 37 toán 11 tập 1
LT – VD 6 trang 37 toán 11 tập 1
Giải phương trình được nêu trong bài toán mở đầu.
Lời giải:
+) Vệ tinh cách mặt đất 1 000 km thì h=1 000
Khi đó
$\begin{array}{l}1000 = 550 + 450.\cos \frac{\pi }{{50}}t\\ \Leftrightarrow \cos \frac{\pi }{{50}}t = 1\\ \Leftrightarrow \cos \frac{\pi }{{50}}t = \cos 0\\ \Leftrightarrow \frac{\pi }{{50}}t = 0 + k2\pi \\ \Leftrightarrow t = 100.k\,\,\,\,;k \in N*\end{array}$
+) Vệ tinh cách mặt đất 250 km thì h=250
Khi đó
$\begin{array}{l}250 = 550 + 450.\cos \frac{\pi }{{50}}t\\ \Leftrightarrow \cos \frac{\pi }{{50}}t = – \frac{2}{3}\\ \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{{50}}t = \arccos \left( { – \frac{2}{3}} \right) + k2\pi \\\frac{\pi }{{50}}t = – \arccos \left( { – \frac{2}{3}} \right) + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}t = \frac{{50}}{\pi }\left[ {\arccos \left( { – \frac{2}{3}} \right) + k2\pi } \right]\\t = \frac{{50}}{\pi }\left[ { – \arccos \left( { – \frac{2}{3}} \right) + k2\pi } \right]\end{array} \right.;k \in N*\end{array}$
+) Vệ tinh cách mặt đất 100 km thì h=100
Khi đó
$\begin{array}{l}100 = 550 + 450.\cos \frac{\pi }{{50}}t\\ \Leftrightarrow \cos \frac{\pi }{{50}}t = – 1\\ \Leftrightarrow \cos \frac{\pi }{{50}}t = \cos \pi \\ \Leftrightarrow \frac{\pi }{{50}}t = \pi + k2\pi \\ \Leftrightarrow t = 50 + 100k\,\,\,\,;k \in N*\end{array}$
HĐ 5 trang 37 toán 11 tập 1
Quan sát giao điểm của đồ thị hàm số y = tan x và đường thẳng y = 1
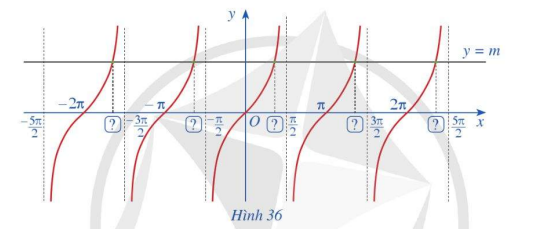
a) Từ hoành độ giao điểm của đồ thị hàm số y = tanx và đường thẳng y = m trên khoảng $\left( { – \frac{\pi }{2};\frac{\pi }{2}} \right)$, hãy xác định tất cả các hoành độ giao điểm của hai đồ thị đó
b) Có nhận xét gì về nghiệm của phương trình tanx = 1
Lời giải:
a) Do hoành độ giao điểm nằm trên khoảng $\left( { – \frac{\pi }{2};\frac{\pi }{2}} \right)$ nên: $\tan x = m \Leftrightarrow \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi $
b) Nhận xét: trên khoảng $\left( { – \frac{\pi }{2};\frac{\pi }{2}} \right)$, với mọi $m \in \mathbb{R}$ ta luôn có $x = \alpha + k\pi $
LT – VD 7 trang 37 toán 11 tập 1
a) Giải phương trình $\tan x = 1$
b) Tìm góc lượng giác x saoo cho $\tan x = \tan {67^ \circ }$
Lời giải:
a) $\tan x = 1 \Leftrightarrow \tan x = \tan \frac{\pi }{4} \Leftrightarrow x = \frac{\pi }{4} + k\pi $
b) $\tan x = \tan {67^ \circ } \Leftrightarrow x = {67^ \circ } + k{.180^ \circ }$
Trang 38 toán 11 tập 1
HĐ 6 trang 38 toán 11 tập 1
Quan sát các giao điểm của đồ thị hàm số y = cotx và đường thẳng y = -1 (Hình 37)
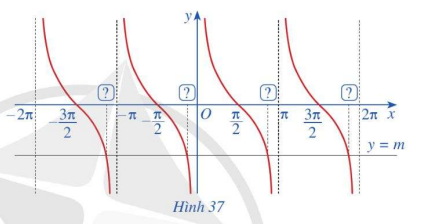
a) Từ hoành độ giao điểm của đồ thị hàm số y = cotx và đường thẳng y = m trên khoảng $\left( {0;\pi } \right)$, hãy xác định tất cả các hoành độ giao điểm của hai đồ thị đó.
b) Có nhận xét gì về nghiệm của phương trình cotx = -1?
Lời giải:
a) Do hoành độ giao điểm nằm trên khoảng $\left( {0;\pi } \right)$ nên: $\cot x = m \Leftrightarrow \cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi $
b) Nhận xét: trên khoảng $\left( {0;\pi } \right)$, với mọi $m \in \mathbb{R}$ ta luôn có $x = \alpha + k\pi $
Trang 39 toán 11 tập 1
LT – VD 8 trang 39 toán 11 tập 1
a) Giải phương trình $\cot x = 1$
b) Tìm góc lượng giác x sao cho $\cot x = \cot \left( { – {{83}^ \circ }} \right)$
Lời giải:
a) $\cot x = 1 \Leftrightarrow \cot x = \cot \frac{\pi }{4} \Leftrightarrow x = \frac{\pi }{4} + k\pi $
b) $\cot x = \cot \left( { – {{83}^ \circ }} \right) \Leftrightarrow x = – {83^ \circ } + k{.180^ \circ }$
Luyện tập 9 trang 39 toán 11 tập 1
Sử dụng MTCT để giải mỗi phương trình sau với kết quả là radian ( làm tròn kết quả đến hàng phần nghìn)
a) $\sin x = 0,2$
b) $\cos x = – \frac{1}{5}$
c) $\tan x = \sqrt 2 $
Lời giải
a) Bấm liên tiếp nút SHIFT, nút SIN, nút 0, nút . , nút 2, nút =
Ta được kết quả gần đúng là 11,537.
Vậy phương trình $\sin x = 0,2$ có các nghiệm là :
$x \approx 11,537 + k2\pi ,k \in Z$ và $x \approx \pi – 11,537 + k2\pi ,k \in Z$
b) Bấm liên tiếp nút SHIFT, nút COS, nút -, nút 1 , nút : ,nút 5; nút =
Ta được kết quả gần đúng là 101,537.
Vậy phương trình $\cos x = – \frac{1}{5}$ có các nghiệm là :
$x \approx 101,537 + k2\pi ,k \in Z$ và $x \approx – 101,537 + k2\pi ,k \in Z$
c) Bấm liên tiếp nút SHIFT, nút TAN, nút căn , nút 2 , nút =
Ta được kết quả gần đúng là 54,736.
Vậy phương trình $\tan x = \sqrt 2 $ có các nghiệm là :
$x \approx 54,736 + k\pi ,k \in Z$
Trang 40 toán 11 tập 1
Bài 1 trang 40 sgk Toán 11 tập 1 Cánh diều
Giải phương trình:
a) $sin(2\pi -\frac{\pi }{3})=-\frac{\sqrt{3}}{2}$;
b) $sin(3x+\frac{\pi }{4})=-\frac{1}{2}$;
c) $cos(\frac{x}{2}+\frac{\pi }{4})=\frac{\sqrt{3}}{2}$;
d) $2cos3x+5=3$;
e) $3tanx=-\sqrt{3}$;
g) $cotx-3=\sqrt{3}(1-cotx)$.
Bài giải:
a) $\sin \left( {2x – \frac{\pi }{3}} \right) = – \frac{{\sqrt 3 }}{2}$
$\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}2x – \frac{\pi }{3} = – \frac{\pi }{3} + k2\pi \\2x – \frac{\pi }{3} = \pi + \frac{\pi }{3} + k2\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}2x = k2\pi \\2x = \frac{{5\pi }}{3} + k2\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x = k\pi \\x = \frac{{5\pi }}{6} + k\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}$
Vậy phương trình có nghiệm là: $x \in \left\{ {k\pi ;\frac{{5\pi }}{6} + k\pi } \right\}$
b) $\sin \left( {3x + \frac{\pi }{4}} \right) = – \frac{1}{2}$
$\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}3x + \frac{\pi }{4} = – \frac{\pi }{6} + k2\pi \\3x + \frac{\pi }{4} = \frac{{7\pi }}{6} + k2\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}3x = – \frac{{5\pi }}{{12}} + k2\pi \\3x = \frac{{11\pi }}{{12}} + k2\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x = – \frac{{5\pi }}{{36}} + k\frac{{2\pi }}{3}\\x = \frac{{11\pi }}{{36}} + k\frac{{2\pi }}{3}\end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}$
c) $\cos \left( {\frac{x}{2} + \frac{\pi }{4}} \right) = \frac{{\sqrt 3 }}{2}$
$\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}\frac{x}{2} + \frac{\pi }{4} = \frac{\pi }{6} + k2\pi \\\frac{x}{2} + \frac{\pi }{4} = – \frac{\pi }{6} + k2\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}\frac{x}{2} = – \frac{\pi }{{12}} + k2\pi \\\frac{x}{2} = – \frac{{5\pi }}{{12}} + k2\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x = – \frac{\pi }{6} + k4\pi \\x = – \frac{{5\pi }}{6} + k4\pi \end{array} \right.\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}$
d) $2\cos 3x + 5 = 3$
$\begin{array}{l} \Leftrightarrow \cos 3x = – 1\\ \Leftrightarrow \left[ \begin{array}{l}3x = \pi + k2\pi \\3x = – \pi + k2\pi \end{array} \right.\,\,\,\,\left( {k \in \mathbb{Z}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{3} + k\frac{{2\pi }}{3}\\x = \frac{{ – \pi }}{3} + k\frac{{2\pi }}{3}\end{array} \right.\,\,\,\,\left( {k \in \mathbb{Z}} \right)\end{array}$
e)
$\begin{array}{l}3\tan x = – \sqrt 3 \\ \Leftrightarrow \tan x = \frac{{ – \sqrt 3 }}{3}\\ \Leftrightarrow \tan x = \tan \left( { – \frac{\pi }{6}} \right)\\ \Leftrightarrow x = – \frac{\pi }{6} + k\pi \end{array}$
g)
$\begin{array}{l}\cot x – 3 = \sqrt 3 \left( {1 – \cot x} \right)\\ \Leftrightarrow \cot x – 3 = \sqrt 3 – \sqrt 3 \cot x\\ \Leftrightarrow \cot x + \sqrt 3 \cot x = \sqrt 3 + 3\\ \Leftrightarrow (1 + \sqrt 3 )\cot x = \sqrt 3 + 3\\ \Leftrightarrow \cot x = \sqrt 3 \\ \Leftrightarrow \cot x = \cot \frac{\pi }{6}\\ \Leftrightarrow x = \frac{\pi }{6} + k\pi \end{array}$
Bài 2 trang 40 sgk Toán 11 tập 1 Cánh diều
Giải phương trình:
a) $sin(2x+\frac{\pi }{4})=sinx$;
b) $sin2x=cos3x$;
c) $cos^{2}2x=cos^{2}(x+\frac{\pi }{6})$.
Bài giải:
a)
$\sin \left( {2x + \frac{\pi }{4}} \right) = \sin x \Leftrightarrow \left[ \begin{array}{l}2x + \frac{\pi }{4} = x + k2\pi \\2x + \frac{\pi }{4} = \pi – x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = – \frac{\pi }{4} + k2\pi \\3x = \pi – \frac{\pi }{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = – \frac{\pi }{4} + k2\pi \\x = \frac{\pi }{4} + \frac{{k2\pi }}{3}\end{array} \right.;k \in Z$
b)
$\begin{array}{l}\sin 2x = \cos 3x\\ \Leftrightarrow \cos 3x = \cos \left( {\frac{\pi }{2} – 2x} \right)\\ \Leftrightarrow \left[ \begin{array}{l}3x = \frac{\pi }{2} – 2x + k2\pi \\3x = – \left( {\frac{\pi }{2} – 2x} \right) + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}5x = \frac{\pi }{2} + k2\pi \\x = – \frac{\pi }{2} + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{{10}} + \frac{{k2\pi }}{5}\\x = – \frac{\pi }{2} + k2\pi \end{array} \right.\end{array}$
c)
$\begin{array}{l}{\cos ^2}2x = {\cos ^2}\left( {x + \frac{\pi }{6}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}\cos 2x = \cos \left( {x + \frac{\pi }{6}} \right)\\\cos 2x = – \cos \left( {x + \frac{\pi }{6}} \right)\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\cos 2x = \cos \left( {x + \frac{\pi }{6}} \right)\\\cos 2x = \cos \left( {\pi – \left( {x + \frac{\pi }{6}} \right)} \right)\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\cos 2x = \cos \left( {x + \frac{\pi }{6}} \right)\\\cos 2x = \cos \left( {\frac{{5\pi }}{6} – x} \right)\end{array} \right.\end{array}$
Với $\cos 2x = \cos \left( {x + \frac{\pi }{6}} \right) \Leftrightarrow \left[ \begin{array}{l}2x = – \left( {x + \frac{\pi }{6}} \right) + k2\pi \\2x = x + \frac{\pi }{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}3x = – \frac{\pi }{6} + k2\pi \\x = \frac{\pi }{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = – \frac{\pi }{{18}} + \frac{{k2\pi }}{3}\\x = \frac{\pi }{6} + k2\pi \end{array} \right.$
Với $\cos 2x = \cos \left( {\frac{{5\pi }}{6} – x} \right) \Leftrightarrow \left[ \begin{array}{l}2x = \frac{{5\pi }}{6} – x + k2\pi \\2x = – \left( {\frac{{5\pi }}{6} – x} \right) + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}3x = \frac{{5\pi }}{6} + k2\pi \\x = – \frac{{5\pi }}{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{{5\pi }}{{18}} + \frac{{k2\pi }}{3}\\x = – \frac{{5\pi }}{6} + k2\pi \end{array} \right.$
Bài 3 trang 40 sgk Toán 11 tập 1 Cánh diều
Dùng đồ thị hàm số $y=sinx, y=cosx$ để xác định số nghiệm của phương trình:
a) $3sinx+2=0$ trên khoảng $(-\frac{5\pi }{2};\frac{5\pi }{2})$;
b) $cosx=0$ trên đoạn $\left [ -\frac{5\pi }{2};\frac{5\pi }{2} \right ]$.
Bài giải:
a) Vẽ đồ thị:
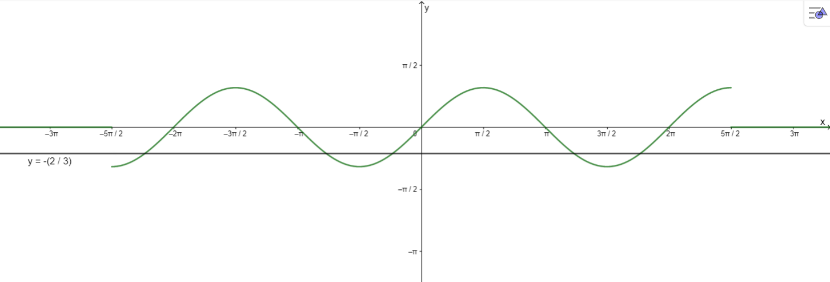
$3\sin x + 2 = 0$ trên đoạn $\left( { – \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)$ có 5 nghiệm
b) Vẽ đồ thị:
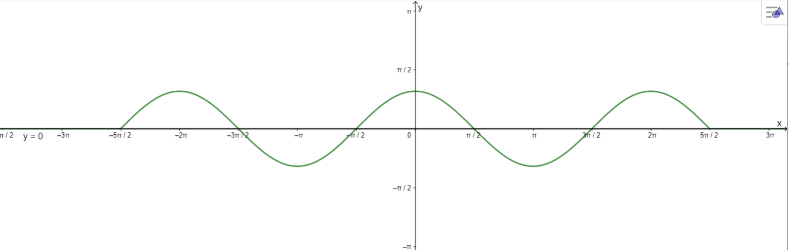
$\cos x = 0$ trên đoạn $\left[ { – \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right]$ có 6 nghiệm
Bài 4 trang 40 sgk Toán 11 tập 1 Cánh diều
Số giờ có ánh sáng mặt trời của một thành phố A ở vĩ độ $40^{\circ}$ Bắc trong ngày thứ $t$ của một năm không nhuận được cho bởi hàm số:
$d(t)=3sin\left [ \frac{\pi }{182}(t-80) \right ]+12$ với $t\in \mathbb{Z}$ và $0< t\leq 365$.
a) Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày nào trong năm?
b) Vào ngày nào trong năm thì thành phố A có đúng 9 giờ có ánh sáng mặt trời?
c) Vào ngày nào trong năm thì thành phố A có đúng 15 giờ có ánh sáng mặt trời?
Bài giải:
a) Thành phố A có đúng 12 giờ có ánh sáng mặt trời thì d(t) = 12.
Khi đó
$\begin{array}{l}12 = 3\sin \left[ {\frac{\pi }{{182}}\left( {t – 80} \right)} \right] + 12\\ \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t – 80} \right)} \right] = 0\\ \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t – 80} \right)} \right] = \sin 0\\ \Leftrightarrow \frac{\pi }{{182}}\left( {t – 80} \right) = k\pi \\ \Leftrightarrow t = 80 + 182k;k \in Z\end{array}$
Mà $t \in \mathbb{Z}$ và $0 < t \le 365$ nên
$\begin{array}{l}0 < 80 + 182k \le 365\\ \Rightarrow 0 \le k \le 1,56\end{array}$
Suy ra $k \in \left\{ {0;1} \right\}$
Khi đó $t \in \left\{ {80;262} \right\}$
Vậy Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày thứ 80 và 262 trong năm
b) Thành phố A có đúng 9 giờ có ánh sáng mặt trời thì d(t) = 9.
Khi đó
$\begin{array}{l}9 = 3\sin \left[ {\frac{\pi }{{182}}\left( {t – 80} \right)} \right] + 12\\ \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t – 80} \right)} \right] = – 1\\ \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t – 80} \right)} \right] = \sin \left( { – \frac{\pi }{2}} \right)\\ \Leftrightarrow \frac{\pi }{{182}}(t – 80) = – \frac{\pi }{2} + k2\pi \\ \Leftrightarrow t = – 11 + 364k;k \in Z\end{array}$
Mà $t \in \mathbb{Z}$ và $0 < t \le 365$ nên
$\begin{array}{l}0 < – 11 + 364k \le 365\\ \Rightarrow 0 < k \le 1,03\end{array}$.
Suy ra $k= 1$.
Khi đó $t= – 11 + 364.1 = 353$.
Vậy Thành phố A có đúng 9 giờ có ánh sáng mặt trời vào ngày thứ 353 trong năm.
c) Thành phố A có đúng 15 giờ có ánh sáng mặt trời thì d(t) = 15.
Khi đó
$\begin{array}{l}15 = 3\sin \left[ {\frac{\pi }{{182}}\left( {t – 80} \right)} \right] + 12\\ \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t – 80} \right)} \right] = 1\\ \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {t – 80} \right)} \right] = \sin \left( {\frac{\pi }{2}} \right)\\ \Leftrightarrow \frac{\pi }{{182}}(t – 80) = \frac{\pi }{2} + k2\pi \\ \Leftrightarrow t = 171 + 364k;k \in Z\end{array}$
Mà $t \in \mathbb{Z}$ và $0 < t \le 365$ nên
$\begin{array}{l}0 < 171 + 364k \le 365\\ \Rightarrow 0 \le k \le 0,53\end{array}$.
Suy ra $k=0$.
Khi đó $t= 171 + 364.0 = 171$.
Vậy Thành phố A có đúng 15 giờ có ánh sáng mặt trời vào ngày thứ 171 trong năm.
Bài 5 trang 40 sgk Toán 11 tập 1 Cánh diều
Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động quanh vị trí cân bằng (Hình 38). Nghiên cứu trò chơi này, người ta thấy khoảng cách $h$ (m) từ vị trí người chơi đu đến vị trí cân bằng được biểu diễn qua thời gian $t$ (s) (với $t\geq 0$) bởi hệ thức $h=\left | d \right |$ với $d=3cos\left [ \frac{\pi }{3}(2t-1) \right ]$, trong đó ta quy ước $d> 0$ khi vị trí cân bằng ở phía sau lưng người chơi đu và $d< 0$ trong trường hợp ngược lại (Nguồn: Đại số và Giải tích 11 Nâng cao, NXBGD Việt Nam, 2020). Vào thời gian $t$ nào thì khoảng cách $h$ là 3 m; 0 m?
Bài giải:

+) Khi khoảng cách từ người chơi đu đến vị trí cân bằng là 3m thì h = 3.
Khi đó
$\begin{array}{l}3 = \left| d \right| = \left| {3\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right]} \right|\\ \Rightarrow \left[ \begin{array}{l}3\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = 3\\3\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = – 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = 1\\\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = – 1\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = \cos 0\\\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = \cos \pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{3}\left( {2t – 1} \right) = k2\pi \\\frac{\pi }{3}\left( {2t – 1} \right) = \pi + k2\pi \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}t = \frac{{6k + 1}}{2}\\t = 3k + 2\end{array} \right.;k \in Z\end{array}$
+) Khi khoảng cách từ người chơi đu đến vị trí cân bằng là 0m thì h = 0.
Khi đó
$\begin{array}{l}0 = \left| d \right| = \left| {3\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right]} \right|\\ \Rightarrow 3\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = 0\\ \Leftrightarrow \cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = 0\\ \Leftrightarrow \cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = 0\\ \Leftrightarrow \cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right] = \cos \frac{\pi }{2}\\ \Leftrightarrow \frac{\pi }{3}\left( {2t – 1} \right) = \frac{\pi }{2} + k\pi \\ \Leftrightarrow t = \frac{5}{4} + \frac{{3k}}{2};k \in Z\end{array}$
