Giải Vật lí 10 trang 83 Bài 21: Moment lực. Cân bằng của vật rắn
Giải Vật lí 10 trang 83 Bài 21: Moment lực. Cân bằng của vật rắn
Giải Vật lí 10 trang 83 Bài 21: Moment lực. Cân bằng của vật rắn sách Kết nối tri thức có đáp án chi tiết cho từng bài tập trong sách giáo khoa vật lí 10 KNTT. Mời các em học sinh cùng quý phụ huynh tham khảo
Vật lí 10 trang 83 bài 21
Câu hỏi 1 trang 83 SGK vật lí 10
Mô tả thao tác dùng búa để nhổ đinh.
Lời giải
Thao tác dùng búa để nhổ đinh: Kẹp cây đinh vào giữa 2 khe nhọn của đầu nhổ đinh, bề mặt đầu đóng đinh vuông góc với mặt phẳng ngang. Dùng tay giữ chặt cán búa, dùng lực để kéo cán búa về phía mình, tạo lực kéo cây đinh lên.
Câu hỏi 2 trang 83 SGK vật lí 10
Lực \(\vec{F}\) nên đặt vào đâu trên cán búa để nhổ đinh được dễ dàng? Khi đó cánh tay đòn (d) của lực lớn hay nhỏ?
Lời giải
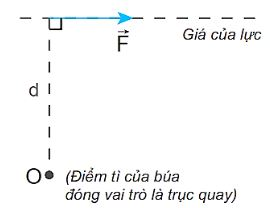
– Để nhổ đinh được dễ dàng, lực \(\vec{F}\) nên đặt vào điểm cuối trên cán búa (điểm xa đầu nhổ đinh nhất).
– Lực \(\vec{F}\) nên có giá vuông góc với cánh tay đòn d để thao tác nhổ đinh sẽ càng dễ hơn
– Khi đó cánh tay đòn d của lực lớn nhất.
Câu hỏi 3 trang 83 SGK vật lí 10
Tác dụng làm quay của lực phụ thuộc những yếu tố nào?
Lời giải
Tác dụng làm quay của lực phụ thuộc vào độ lớn của lực và cánh tay đòn.
Câu hỏi 4 trang 83 SGK vật lí 10
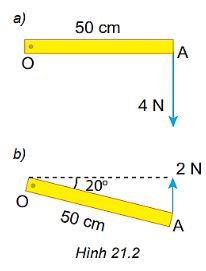
Hình 21.2 mô tả một chiếc thước mảnh OA, đồng chất, dài 50 cm, có thể quay quanh trục quay cố định ở đầu O.
Trong các tình huống ở Hình 21.2a, b thước OA quay theo chiều kim đồng hồ hay ngược chiều kim đồng hồ?
Lời giải
Trong tình huống ở Hình 21.2a thước OA quay theo chiều kim đồng hồ.
Trong tình huống ở Hình 21.2b thước OA quay ngược chiều kim đồng hồ.
Câu hỏi trang 83 SGK vật lí 10
Hình 21.2 mô tả một chiếc thước mảnh OA, đồng chất, dài 50 cm, có thể quay quanh trục quay cố định ở đầu O.
Tính moment lực ứng với mỗi tình huống trong Hình 21.2.
Đổi 50 cm = 0,5 m
– Moment lực trong Hình 21.2a: M = F.d = 4.0,5 = 2 N.
– Moment lực trong Hình 21.2b: M = F.d = 2.0,5.cos 20o ≈ 0,94 N.
Vật lí 10 trang 84 bài 21
Câu hỏi 1 trang 84 SGK vật lí 10
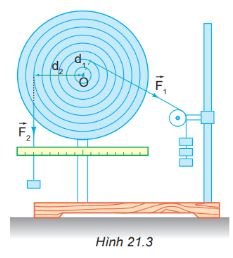
Nếu bỏ lực \(\vec{F_{1} }\) thì đĩa quay theo chiều nào?
Lời giải
Nếu bỏ lực \(\vec{F_{1} }\) thì đĩa quay ngược chiều kim đồng hồ.
Câu hỏi 2 trang 84 SGK vật lí 10
Nếu bỏ lực \(\vec{F_{2} }\) thì đĩa quay theo chiều nào?
Lời giải
Nếu bỏ lực \(\vec{F_{2} }\) thì đĩa quay theo chiều kim đồng hồ.
Câu hỏi 3 trang 84 SGK vật lí 10
Khi đĩa cân bằng lập tích F1.d1 và F2.d2 rồi so sánh.
Lời giải
Coi khối lượng mỗi quả nặng là 1 đơn vị, dựa vào hình vẽ ta có thể tính được các tích:
F1d1 = 3.2 = 6
F2d2 = 1.6 = 6
Khi đĩa cân bằng, ta có F1.d1 = F2.d2
Câu hỏi 4 trang 84 SGK vật lí 10
a) Sử dụng kiến thức về moment lực giải thích vì sao chiếc bập bênh đứng cân bằng.
b) Cho biết người chị (bên phải) có trọng lượng P2 = 300 N, khoảng cách d2 = 1 m, còn người em có trọng lượng P1 = 200 N. Hỏi khoảng cách d1 phải bằng bao nhiêu để bập bênh bằng nằm ngang?
Lời giải
a) Chiếc bập bênh có thể đứng cân bằng vì tổng các moment lực tác dụng lên trục quay của chiếc bập bênh bằng không.
+ Moment lực do người chị gây ra có tác dụng làm cho bập bênh quay cùng chiều kim đồng hồ.
+ Momen lực do người em gây ra có tác dụng làm cho bập bênh quay ngược chiều kim đồng hồ.
Do đó, hai moment lực này cân bằng.
b) Để bập bênh cân bằng, tổng các moment lực tác dụng lên bập bênh phải bằng 0.
Hay: P2.d2 = P1.d1 ⇒ d1 = \(\frac{P2.d2}{P1}\)= \(\frac{300.1}{200}\) = 1,5 m
Vậy để bập bênh cân bằng thì khoảng cách d1 phải bằng 1,5 m.
IV. Điều kiện cân bằng tổng quát của vật rắn
Vật lí 10 trang 85 bài 21
Câu hỏi trang 85 vật lí 10
Áp dụng điều kiện cân bằng tổng quát vào thanh cứng tựa tường (Hình 21.8).
a) Viết điều kiện cân bằng thứ nhất.
b) Viết điều kiện cân bằng thứ hai đối với trục quay A.

Lời giải
a) Điều kiện cân bằng thứ nhất là: Tổng các lực tác dụng lên thanh cứng bằng 0.
\(\vec{F_{msn} } + \vec{N_{A} } + \vec{P} + \vec{N_{B} } = \vec{0}\)
b) Điều kiện câng bằng thứ hai đối với trục quay A là: Tổng các moment lực tác dụng lên thanh cứng đối với trục quay A bằng 0
\(M_{\vec{N_{B} } } = M_{\vec{P} } \Leftrightarrow N_{B} .h = P\frac{d}{2}\)
