Bài 5. Elip Chuyên đề học tập Toán 10

Giải Bài 5 Elip Chuyên đề học tập Toán 10. Hướng dẫn giải bài tập theo từng bước, dễ hiểu sách chuyên đề học tập toán 10 Kết nối tri thức

HĐ1 Chuyên đề học tập Toán 10

Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (H.3.1)

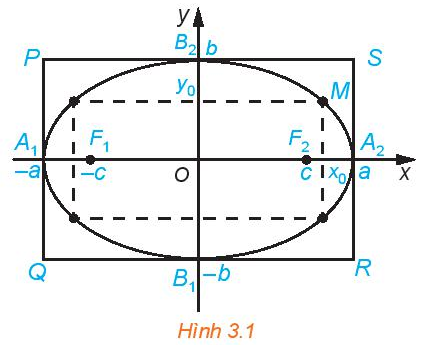
a) Tìm tọa độ các giao điểm của elip với các trục tọa độ

b) Hãy giải thích vì sao, nếu điểm \(M({x_0};{y_0})\) thuộc elip thì các điểm có tọa độ \(({x_0}; – {y_0}),( – {x_0};{y_0}),( – {x_0}; – {y_0})\) cũng thuộc Elip.

c) Với điểm \(M({x_0};{y_0})\) thuộc elip, hãy so sánh \(O{M^2}\) với \({a^2},{b^2}\)

Lời giải chi tiết:

a)

\(y = 0 \Rightarrow \frac{{{x^2}}}{{{a^2}}} = 1 \Rightarrow x = \pm a\)

Giao điểm của elip với Ox là \({A_1}\left( { – a;0} \right),{A_2}\left( {a;0} \right).\)

\(x = 0 \Rightarrow \frac{{{y^2}}}{{{b^2}}} = 1 \Rightarrow y = \pm b\)

Giao điểm của elip với Oy là \({B_1}\left( {0; – b} \right),{B_2}\left( {0;b} \right).\)

b) Nếu điểm \(M({x_0};{y_0})\) thuộc elip thì \(\frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} = 1\)

\( \Rightarrow \frac{{{x_0}^2}}{{{a^2}}} + \frac{{{{( – {y_0})}^2}}}{{{b^2}}} = 1;\frac{{{{( – {x_0})}^2}}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} = 1;\frac{{{{( – {x_0})}^2}}}{{{a^2}}} + \frac{{{{( – {y_0})}^2}}}{{{b^2}}} = 1\)

hay các điểm có tọa độ \(({x_0}; – {y_0}),( – {x_0};{y_0}),( – {x_0}; – {y_0})\) cũng thuộc Elip.

c) Từ H.3.1 dễ thấy \(a > b\)

\(\begin{array}{l} \Rightarrow \frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{a^2}}} \le \frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} \le \frac{{{x_0}^2}}{{{b^2}}} + \frac{{{y_0}^2}}{{{b^2}}}\\ \Leftrightarrow \frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{a^2}}} \le 1 \le \frac{{{x_0}^2}}{{{b^2}}} + \frac{{{y_0}^2}}{{{b^2}}}\\ \Leftrightarrow {b^2} \le {x_0}^2 + {y_0}^2 \le {a^2}\\ \Leftrightarrow {b^2} \le O{M^2} \le {a^2}\end{array}\)

 Luyện tập 1 Chuyên đề học tập Toán 10

Viết phương trình chính tắc của elip với độ dài trục lớn bằng 10 và tiêu cự bằng 6.

Lời giải chi tiết:

Ta có:

+ Độ dài trục lớn: \(2a = 10 \Rightarrow a = 5\)

+ Tiêu cự: \(2c = 2\sqrt {{a^2} – {b^2}} = 6 \Rightarrow \sqrt {{5^2} – {b^2}} = 3 \Rightarrow {b^2} = 16\)

Phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)

 Luyện tập 2 Chuyên đề học tập Toán 10

(Phép co đường tròn) Cho đường tròn có phương trình \({x^2} + {y^2} = {a^2}\) và số k \((0 < k < 1)\). Với mỗi điểm \(M({x_0};{y_0})\) thuộc đường tròn, gọi \(H({x_0};0)\) là hình chiếu vuông góc của M lên trục Ox và N là điểm thuộc đoạn MH sao cho \(HN = kHM\) (H.3.5)

a) Tính tọa độ của N theo \({x_0};{y_0};k.\)

b) Chứng minh rằng khi điểm M thay đổi trên đường tròn thì N thay đổi trên Elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{{(ka)}^2}}} = 1\)

Lời giải chi tiết:

Gọi \(N({x_N};{y_N})\).

N thuộc đoạn MH và \(HN = kHM \Rightarrow \overrightarrow {HN} = k\overrightarrow {HM} \)

\(\begin{array}{l} \Leftrightarrow ({x_N} – {x_0};{y_N}) = k(0;{y_0})\\ \Leftrightarrow \left\{ \begin{array}{l}{x_N} – {x_0} = k.0\\{y_N} = k.{y_0}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_N} = {x_0}\\{y_N} = k.{y_0}\end{array} \right.\end{array}\)

Vì \(M({x_0};{y_0})\) thuộc (C) \({x^2} + {y^2} = {a^2}\) nên

\({x_0}^2 + {y_0}^2 = {a^2} \Leftrightarrow {x_N}^2 + {\left( {\frac{{{y_N}}}{k}} \right)^2} = {a^2} \Leftrightarrow \frac{{{x_N}^2}}{{{a^2}}} + \frac{{{y_N}^2}}{{{{(ka)}^2}}} = 1\)

Vậy N thuộc Elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{{(ka)}^2}}} = 1\)

HĐ2 Chuyên đề học tập Toán 10

Cho Elip có hai tiêu điểm \({F_1}( – c;0),{F_2}(c;0)\) và độ dài trục lớn bằng 2a và điểm \(M(x;y)\).

a) Tính \(M{F_1}^2 – M{F_2}^2\)

b) Khi điểm M thuộc Elip (\(M{F_1} + M{F_2} = 2a\)), tính \(M{F_1} – M{F_2},M{F_1},M{F_2}.\)

Lời giải chi tiết:

a) Tính \(M{F_1}^2 – M{F_2}^2\)

Ta có: \(\overrightarrow {M{F_1}} ( – c – x; – y);\overrightarrow {M{F_2}} (c – x; – y)\)

\( \Rightarrow M{F_1}^2 = {( – c – x)^2} + {( – y)^2};M{F_2}^2 = {(c – x)^2} + {( – y)^2}\)

\( \Rightarrow M{F_1}^2 – M{F_2}^2 = {( – c – x)^2} – {(c – x)^2} = 4cx\)

b) Khi điểm M thuộc Elip (\(M{F_1} + M{F_2} = 2a\)),

\(\begin{array}{l}M{F_1} – M{F_2} = \frac{{M{F_1}^2 – M{F_2}^2}}{{M{F_1} + M{F_2}}} = \frac{{2c}}{a}x\\M{F_1} = \frac{{2a + \frac{{2c}}{a}x}}{2} = a + \frac{c}{a}x\\M{F_2} = \frac{{2a – \frac{{2c}}{a}x}}{2} = a – \frac{c}{a}x\end{array}\)

Luyện tập 3 Chuyên đề học tập Toán 10

Cho elip \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{20}} = 1\), điểm M thay đổi trên elip. Hỏi khoảng cách từ M tới một tiêu điểm của elip lớn nhất bằng bao nhiêu, nhỏ nhất bằng bao nhiêu?

Lời giải chi tiết:

Ta có: \({a^2} = 36,{b^2} = 20 \Rightarrow a = 6,b = 2\sqrt 5 \Rightarrow c = \sqrt {{a^2} – {b^2}} = 4\)

Xét tiêu điểm \({F_1}( – 4;0)\)

\(M{F_1}\) nhỏ nhất bằng \(a – c = 2\) khi M trùng \({A_1}( – 6;0)\)

\(M{F_1}\) lớn nhất bằng \(a + c = 10\) khi M trùng \({A_2}(6;0)\)

  Vận dụng 1 Chuyên đề học tập Toán 10

Với thông tin đưa ra trong tình huống mở đầu, lập phương trình chính tắc của elip quỹ đạo của Trái Đất, với 1 đơn vị đo trên mặt phẳng tọa độ ứng với \({10^6}km\) trên thực tế.

Lời giải chi tiết:

Coi tâm mặt trời là gốc tọa độ O.

Gọi PTCT của elip quỹ đạo của Trái Đất là (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)

M là vị trí của Trái Đất, rõ ràng \(M \in (E)\)

Vì \(b \le OM \le a\) nên \(a = {152.10^6};b = {147.10^6}\)

\( \Rightarrow \) Phương trình chính tắc của elip quỹ đạo của Trái Đất là (E): \(\frac{{{x^2}}}{{{{23104.10}^{12}}}} + \frac{{{y^2}}}{{{{21609.10}^{12}}}} = 1\)

 Hoạt động 3 Chuyên đề học tập Toán 10

Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), với các tiêu điểm \({F_1}( – c;0),{F_2}(c;0),\)ở đây \(c = \sqrt {{a^2} – {b^2}} \) (H.3.6). Xét các đường thẳng \({\Delta _1}:x = – \frac{{{a^2}}}{c}\) và \({\Delta _2}:x = \frac{{{a^2}}}{c}\).

Với điểm M (x; y) thuộc elip, tính các tỉ số \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}}\) và \(\frac{{M{F_2}}}{{d(M,{\Delta _2})}}\) theo a và c.

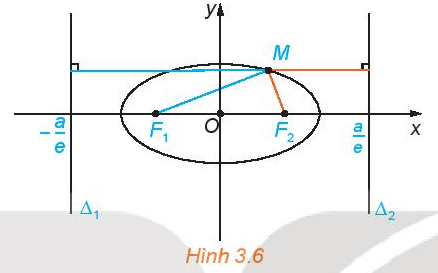
Lời giải chi tiết:

\(M{F_1} = a + \frac{c}{a}x = \frac{{{a^2} + cx}}{a};\;\;M{F_2} = a – \frac{c}{a}x = \frac{{{a^2} – cx}}{a}\)

\(d(M,{\Delta _1}) = \frac{{{a^2}}}{c} + x = \frac{{{a^2} + cx}}{c}\)

\(d(M,{\Delta _2}) = \frac{{{a^2}}}{c} – x = \frac{{{a^2} – cx}}{c}\)

\( \Rightarrow \frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{{a^2} + cx}}{a}:\frac{{{a^2} + cx}}{c} = \frac{c}{a}\) ; \(\frac{{M{F_2}}}{{d(M,{\Delta _2})}} = \frac{{{a^2} – cx}}{a}:\frac{{{a^2} – cx}}{c} = \frac{c}{a}\)

Vậy \(\frac{{M{F_1}}}{{d(M,{\Delta _1})}} = \frac{{M{F_2}}}{{d(M,{\Delta _2})}} = \frac{c}{a}.\)

Luyện tập 4 Chuyên đề học tập Toán 10

Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{25}} = 1\). Tìm tâm sai và các đường chuẩn của elip. Tính các bán kính qua tiêu của điểm M thuộc elip và có hoành độ bằng -2.

Lời giải chi tiết:

Ta có phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{25}} = 1\).

\( \Rightarrow a = 6,b = 5,c = \sqrt {{a^2} – {b^2}} = \sqrt {11} \)

+ Tâm sai của elip: \(e = \frac{{\sqrt {11} }}{6}\)

+ Đường chuẩn: \({\Delta _1}:x = – \frac{{36\sqrt {11} }}{{11}}\) và \({\Delta _2}:x = \frac{{36\sqrt {11} }}{{11}}\).

+ Bán kính qua tiêu của M (-2; y): \(M{F_1} = 6 + \frac{{\sqrt {11} }}{6}.( – 2) = 6 – \frac{{\sqrt {11} }}{3},\;M{F_2} = 6 – \frac{{\sqrt {11} }}{6}.( – 2) = 6 + \frac{{\sqrt {11} }}{3}.\)

Vận dụng 2 Chuyên đề học tập Toán 10

Mặt trăng chuyển động theo một quỹ đạo hình elip nhận tâm Trái Đất là một tiêu điểm. Các khoảng cách lớn nhất và nhỏ nhất từ các vị trí của Mặt Trăng đến tâm Trái Đất tương ứng là 400 000 km và 363 000 km (theo nssdc.gsfc.nasa.gov). Tìm tâm sai của quỹ đạo elip.

Lời giải chi tiết:

Gọi PTCT của quỹ đạo hình elip đó là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\),

Giả sử Trái Đất là tiêu điểm \({F_1}( – c;0)\).

Điểm M bất kì thuộc elip là vị trí của Mặt trăng trong quỹ đạo, khi đó:

\(M{F_1}\) nhỏ nhất bằng \(a – c = 363\;000\)

\(M{F_1}\) lớn nhất bằng \(a + c = 400\;000\)

\( \Rightarrow a = 381500,\;c = 18500\)

\( \Rightarrow \)Tâm sai của elip là: \(e = \frac{{18500}}{{381500}} = \frac{{37}}{{763}}.\)

Giải bài 3.1 trang 44 Chuyên đề học tập Toán 10

Cho elip \(\frac{{{x^2}}}{{12}} + \frac{{{y^2}}}{4} = 1\)

a) Xác định các đỉnh và độ dài các trục của elip

b) Xác định tâm sai và các đường chuẩn của elip

c) Tính bán kính qua tiêu của điểm M thuộc elip, biết điểm M có hoành độ bằng -3.

Lời giải chi tiết

Ta có phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{12}} + \frac{{{y^2}}}{4} = 1\).

\( \Rightarrow a = 2\sqrt 3 ,b = 2,c = \sqrt {{a^2} – {b^2}} = 2\sqrt 2 \)

a)

+ 4 đỉnh: \({A_1}\left( { – 2\sqrt 3 ;0} \right),{A_2}\left( {2\sqrt 3 ;0} \right),\)\({B_1}\left( {0; – 2} \right),{B_2}\left( {0;2} \right).\)

+ Độ dài trục lớn: \(2a = 4\sqrt 3 \), độ dài trục nhỏ: \(2b = 4.\)

b)+ Tâm sai của elip: \(e = \frac{{2\sqrt 2 }}{{2\sqrt 3 }} = \frac{{\sqrt 6 }}{3}\)

+ Đường chuẩn: \({\Delta _1}:x = – \frac{{2\sqrt 3 }}{{\frac{{\sqrt 6 }}{3}}} = – 3\sqrt 2 \) và \({\Delta _2}:x = 3\sqrt 2 \).

c) Bán kính qua tiêu của M (x; y):

\(M{F_1} = 2\sqrt 3 + \frac{{\sqrt 6 }}{3}.( – 3) = 2\sqrt 3 – \sqrt 6 ,\;M{F_2} = 2\sqrt 3 – \frac{{\sqrt 6 }}{3}.( – 3) = 2\sqrt 3 + \sqrt 6 .\)

 Giải bài 3.2 trang 44 Chuyên đề học tập Toán 10

Viết phương trình chính tắc của elip trong mỗi trường hợp sau:

a) Độ dài trục lớn bằng 8, tiêu cự bằng 6.

b) Độ dài trục lớn bằng 8 và tâm sai bằng \(\frac{{\sqrt 3 }}{2}\).

Lời giải chi tiết

a)

+ Độ dài trục lớn bằng \(2a = 8 \Rightarrow a = 4\),

+ Tiêu cự bằng \(2c = 2\sqrt {{a^2} – {b^2}} = 6 \Rightarrow {b^2} = 7\).

\( \Rightarrow \) PTCT của elip \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{7} = 1\)

b)

+ Độ dài trục lớn bằng \(2a = 8 \Rightarrow a = 4\),

+ Tâm sai của elip: \(e = \frac{c}{a} = \frac{{\sqrt 3 }}{2} \Rightarrow c = 2\sqrt 3 \Rightarrow b = 2\)

\( \Rightarrow \) PTCT của elip \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{4} = 1\)

Giải bài 3.3 trang 44 Chuyên đề học tập Toán 10

Cho elip \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{5} = 1\)

a) Qua tiêu điểm của elip vẽ đường thẳng vuông góc với trục Ox, cắt elip tại hai điểm A và B. Tính độ dài của đoạn thẳng AB.

b) Tìm điểm M trên elip sao cho \(M{F_1} = 2M{F_2}\) với \({F_1}\) and \({F_2}\) là hai tiêu điểm của elip (độ hoàn thành của \( {F_1}\) âm).

Lời giải chi tiết

a) Ta có PTCT của elip là: \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{5} = 1\).

\( \Rightarrow a = 3,b = \sqrt 5 ,c = 2\). Tiêu điểm \({F_1}( – 2;0),{F_2}(2;0)\) .

Do hai tiêu điểm đối xứng nhau qua O(0;0) nên ta chỉ cần khảo sát đường thẳng qua một tiêu điểm.

Gọi d là đường thẳng đi qua \({F_2}(2;0)\) góc với trục Ox, cắt elip tại A và B.

Khi đó \(d:x = 2\) và \(A\left( {2;{y_A}} \right),B\left( {2;{y_B}} \right)\) và \(AB = 2.|{y_A}|\).

Vì A thuộc elip nên \(\frac{{{2^2}}}{9} + \frac{{{y_A}^2}}{5} = 1 \Rightarrow \left| {{y_A}} \right | = \frac{5}{3}\).

Do đó chiều dài đoạn AB là \(\frac{{10}}{3}\).

b) Ta có: \(M{F_1} = a + \frac{c}{a}{x_M},\;M{F_2} = a – \frac{c}{a}{x_M}.\)

Mà \(a = 3\), \(c = 2\), \(M{F_1} = 2M{F_2}\) nên:

\(\begin{array}{l}3 + \frac{2}{3}{x_M} = 2.\left( {3 – \frac{2}{3}.{x_M}} \right)\\3 + \frac{2}{3}{x_M} = 6 – \frac{4}{3}{x_M}\\ \Rightarrow {x_M}\left( {\frac{2}{3} + \frac{4}{3}} \right) = 6 – 3\\ \Rightarrow {x_M} = \frac{3}{2}.\end{array}\)

Vì \(M\) thuộc elip nên \({\frac{{\left( {\frac{3}{2}} \right)}}{9}^2} + \frac{{{y^2}}}{5} = 1 \Rightarrow \frac{{{y^2}}}{5} = \frac{3}{4} \Rightarrow y = \pm \frac{{\sqrt {15} }}{2}\).

Do đó có hai điểm M thỏa mãn, có tọa độ là \(\left( {\frac{3}{2};\frac{{\sqrt {15} }}{2}} \right),\left( {\frac{3}{2}; – \frac{{\sqrt {15} }}{2}} \right)\).

Giải bài 3.4 trang 45 Chuyên đề học tập Toán 10

Đường tròn phụ của hình elip là đường tròn có đường kính là trục nhỏ của elip (H.3.8). Do đó, đường tròn phụ là đường tròn lớn nhất có thể nằm bên trong một hình elip. Tìm phương trình đường tròn phụ của elip \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) và chứng minh rằng, nếu điểm \(M({x_0};{y_0})\) thuộc elip thì điểm \(N(\frac{b}{a}{x_0};{y_0})\) thuộc đường tròn phụ.

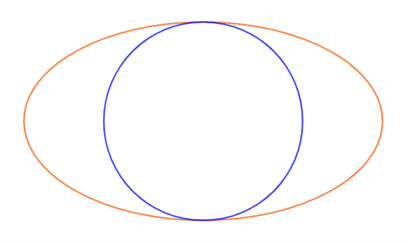
Lời giải chi tiết

PTCT của elip là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)

\( \Rightarrow \) Độ dài trục nhỏ là 2b.

Đường tròn phụ tâm O(0;0), đường kính 2b là: \({x^2} + {y^2} = {b^2}\)

Nếu \(M({x_0};{y_0})\) thuộc elip thì \(\frac{{{x_0}^2}}{{{a^2}}} + \frac{{{y_0}^2}}{{{b^2}}} = 1 \Leftrightarrow \frac{{{b^2}}}{{{a^2}}}{x_0}^2 + {y_0}^2 = {b^2}\) hay \({\left( {\frac{b}{a}{x_0}} \right)^2} + {y_0}^2 = {b^2}\)

\( \Rightarrow \) \(N(\frac{b}{a}{x_0};{y_0})\) thuộc đường tròn phụ.

Giải bài 3.5 trang 45 Chuyên đề học tập Toán 10

Với tâm sai khoảng 0,244, quỹ đạo elip của sao Diêm Vương “dẹt” hơn so với quỹ đạo của tám hành tinh trong hệ mặt trời (xem Em có biết? ở cuối bài). Nửa độ dài trục lớn của elip quỹ đạo là khoảng \(590\;{635.10^6}\)km. Tìm khoảng cách gần nhất và khoảng cách xa nhất giữa sao diêm vương và tâm mặt trời (tiêu điểm của quỹ đạo) (theo nssdc.gsfc.nasa.gov).

Lời giải chi tiết

\frac{{{y^2}}}{{{b^2}}} = 1\),

+ Nửa độ dài trục lớn: \(a = 590\;{635.10^6}\)

+ Tâm sai của elip: \(e = \frac{c}{a} = 0,244 \Rightarrow c = 14\;411\;{494.10^4}\)

Giả sử Mặt trời là tiêu điểm \({F_1}( – c;0)\).

Điểm M bất kì thuộc elip là vị trí của sao Diêm Vươn trong quỹ đạo, khi đó:

\(M{F_1}\) nhỏ nhất bằng \(a – c = 44\;652\;{006.10^4}\)

\(M{F_1}\) lớn nhất bằng \(a + c = 73\;474\;{994.10^4}\)

Vậy khoảng cách gần nhất và xa nhất là \(44\;652\;{006.10^4}\) km và \(73\;474\;{994.10^4}\) km.

Giải bài 3.6 trang 45 Chuyên đề học tập Toán 10

Một phòng thì thầm có trần vòm elip với hai tiêu điểm ở độ cao 1,6m (so với mặt sàn) và cách nhau 16m. Đỉnh của mái vòm cao 7,6 m (H.3.9). Hỏi âm thanh thì thầm từ một tiêu điểm thì sau bao nhiêu giây đến được tiêu điểm kia? Biết vận tốc âm thanh là 343,2 m/s và làm tròn đáp số tới 4 chữ số sau dấu phẩy.

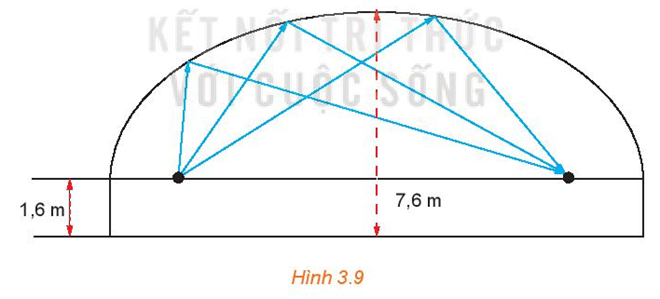
Lời giải chi tiết

Gọi PTCT của mái vòm đó là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\),

+ Khoảng cách giữa 2 tiêu điểm: 2c = 16 (m) \( \Rightarrow c = 8\)

+ Nửa độ dài trục nhỏ là \(b = 7,6 – 1,6 = 6.\)

\( \Rightarrow a = \sqrt {{c^2} + {b^2}} = 10\)

+ M bất kì thuộc elip, ta có: \(M{F_1} + M{F_2} = 2a\) (\({F_1},{F_2}\) là hai tiêu điểm)

Quãng đường âm thanh thì thầm từ tiêu điểm này đến tiêu điểm kia là \(20(m)\)

Thời gian âm thanh thì thầm từ tiêu điểm này đến tiêu điểm kia là: \(\frac{{20}}{{343,2}} \approx 0,0583\;(s)\)

Vậy mất khoảng 0,0583 giây để âm thanh thì thầm từ tiêu điểm này đến được tiêu điểm kia.