Bài tập cuối chuyên đề 1 Chuyên đề học tập Toán 10
Bài tập cuối chuyên đề 1 Chuyên đề học tập Toán 10
Giải Bài tập cuối chuyên đề 1 Chuyên đề học tập Toán 10. Hướng dẫn giải bài tập theo từng bước, dễ hiểu sách chuyên đề học tập toán 10 Kết nối tri thức
Giải bài 1.15 trang 23 Chuyên đề học tập Toán 10
Giải các hệ phương trình sau:
a) \(\left\{ \begin{array}{l}x + y + z = 6\\x + 2y + 3z = 14\\3x – 2y – z = – 4\end{array} \right.\)
b) \(\left\{ \begin{array}{l}2x – 2y + z = 6\\3x + 2y + 5z = 7\\7x + 3y – 6z = 1\end{array} \right.\)
c) \(\left\{ \begin{array}{l}2x + y – 6z = 1\\3x + 2y – 5z = 5\\7x + 4y – 17z = 7\end{array} \right.\)
d) \(\left\{ \begin{array}{l}5x + 2y – 7z = 6\\2x + 3y + 2z = 7\\9x + 8y – 3z = 1\end{array} \right.\)
Lời giải chi tiết
a) Dùng máy tính cầm tay, giải hệ pt ta được nghiệm\((x;y;z) = (1;2;3)\)
b) Dùng máy tính cầm tay, giải hệ pt ta được nghiệm\((x;y;z) = \left( {\frac{{79}}{{55}}; – \frac{{178}}{{165}};\frac{{32}}{{33}}} \right)\)
c) Dùng máy tính cần tay, ta biết phương trình có vô số nghiệm.
Ta tìm tập nghiệm bằng phương pháp Gauss:
\(\left\{ \begin{array}{l}2x + y – 6z = 1\\3x + 2y – 5z = 5\\7x + 4y – 17z = 7\end{array} \right.\)
Nhân phương trình thứ nhất với 2 và cộng với phương trình thứ hai theo từng vế tương ứng, ta được hệ phương trình:
\(\left\{ \begin{array}{l}2x + y – 6z = 1\\7x + 4y – 17z = 7\\7x + 4y – 17z = 7\end{array} \right.\)
Nhận thấy phương trình thứ hai và thứ ba của hệ giống nhau. Như vậy ta được hệ tương đương
\(\left\{ \begin{array}{l}2x + y – 6z = 1\\7x + 4y – 17z = 7\end{array} \right.\)
Nhân phương trình thứ nhất với -3 rồi cộng với PT thứ hai theo từng vế tương ứng ta được:
\(\left\{ \begin{array}{l}2x + y – 6z = 1\\x + y + z = 4\end{array} \right.\)
Nhân phương trình thứ hai với -2 rồi cộng với PT thứ nhất theo từng vế tương ứng ta được:
\(\left\{ \begin{array}{l} – y – 8z = – 7\\x + y + z = 4\end{array} \right.\)
Từ phương trình thứ nhất, ta có: \(y = – 8z + 7\)
Thay vào phương trình thứ hai, ta được: \(x – 8z + 7 + z = 4 \Rightarrow x = 7z – 3\)
Vậy tập nghiệm của hệ phương trình đã cho là \(S = \{ (7z – 3; – 8z + 7;z)|z \in \mathbb{R}\} \)
d) Dùng máy tính cần tay, ta biết phương trình vô nghiệm.
Ta kiểm tra lại bằng phương pháp Gauss:
\(\left\{ \begin{array}{l}5x + 2y – 7z = 6\\2x + 3y + 2z = 7\\9x + 8y – 3z = 1\end{array} \right.\)
Nhân phương trình thứ hai với 2 rồi cộng với phương trình thứ nhất theo từng vế tương ứng, ta được:
\(\left\{ \begin{array}{l}9x + 8y – 3z = 20\\2x + 3y + 2z = 7\\9x + 8y – 3z = 1\end{array} \right.\)
Từ phương trình thứ nhất và thứ ba ta suy ra \(20 = 1\) (Vô lí).
Vậy phương trình đã cho vô nghiệm.
Giải bài 1.16 trang 23 Chuyên đề học tập Toán 10
Tìm các số thực A, B và C thỏa mãn
\(\frac{1}{{{x^3} + 1}} = \frac{A}{{x + 1}} + \frac{{Bx + C}}{{{x^2} – x + 1}}\)
Lời giải chi tiết
Ta có
\(\begin{array}{l}\frac{A}{{x + 1}} + \frac{{Bx + C}}{{{x^2} – x + 1}} = \frac{{A.({x^2} – x + 1)}}{{{x^3} + 1}} + \frac{{\left( {Bx + C} \right).(x + 1)}}{{{x^3} + 1}}\\ = \frac{{A.({x^2} – x + 1) + \left( {Bx + C} \right).(x + 1)}}{{{x^3} + 1}} = \frac{{(A + B){x^2} + (B + C – A)x + A + C}}{{{x^3} + 1}}\\ \Rightarrow (A + B){x^2} + (B + C – A)x + A + C = 1\\ \Leftrightarrow \left\{ \begin{array}{l}A + B = 0\\B + C – A = 0\\A + C = 1\end{array} \right.\end{array}\)
Dùng máy tính cầm tay giải hệ pt ta được \(A = \frac{1}{3};B = – \frac{1}{3};C = \frac{2}{3}.\)
Giải bài 1.17 trang 23 Chuyên đề học tập Toán 10
Tìm parabol \(y = a{x^2} + bx + c\) trong mỗi trường hợp sau:
a) Parabol đi qua ba điểm A(2;-1), B(4;3) và C(-1;8);
b) Parabol nhận đường thẳng \(x = \frac{5}{2}\) làm trục đối xứng và đi qua hai điểm M(1;0), N(5;-4).
Lời giải chi tiết
a) \(A(2; – 1) \in \) parabol nên ta có: \( – 1 = a{.2^2} + b.2 + c\) hay \(4a + 2b + c = – 1\)
Tương tự, parabol đi qua B(4;3) và C(-1;8) nên:
\(3 = a{.4^2} + b.4 + c\) hay \(16a + 4b + c = 3\)
\(8 = a.{( – 1)^2} + b.( – 1) + c\) hay \(a – b + c = 8\)
Ta có hệ phương trình:
\(\left\{ \begin{array}{l}4a + 2b + c = – 1\\16a + 4b + c = 3\\a – b + c = 8\end{array} \right.\)
Dùng máy tính cầm tay giải HPT, ta được a = 1, b = -4, c = 3.
Vậy parabol cần tìm là: \(y = {x^2} – 4x + 3\)
b)
Parabol nhận \(x = \frac{5}{2}\) làm trục đối xứng nên \( – \frac{b}{{2a}} = \frac{5}{2}\) hay \(5a + b = 0\)
M(1;0) thuộc parabol nên ta có: \(0 = a{.1^2} + b.1 + c\) hay \(a + b + c = 0\)
N(5;-4) thuộc parabol nên ta có: \( – 4 = a{.5^2} + b.5 + c\) hay \(25a + 5b + c = – 4\)
Từ đó ta có hệ phương trình
\(\left\{ \begin{array}{l}5a + b = 0\\a + b + c = 0\\25a + 5b + c = – 4\end{array} \right.\)
Dùng máy tính cầm tay giải HPT, ta được a = -1, b = 5, c = -4.
Vậy parabol cần tìm là: \(y = – {x^2} + 5x – 4\)
Giải bài 1.18 trang 23 Chuyên đề học tập Toán 10
Trong mặt phẳng tọa độ, viết phương trình đường tròn đi qua ba điểm A(0;1), B(2;3) và C(4;1)
Lời giải chi tiết
Gọi phương trình đường tròn (I) đi qua 3 điểm A, B, C là: \({x^2} + {y^2} + 2ax + 2by + c = 0\)
\(A\left( {0;1} \right) \in (I):1 + 2b + c = 0\) hay \(2b + c = – 1\)
\(B\left( {2;3} \right) \in (I):4 + 9 + 4a + 6b + c = 0\) hay \(4a + 6b + c = – 13\)
\(C\left( {4;1} \right) \in (I):16 + 1 + 8a + 2b + c = 0\) hay \(8a + 2b + c = – 17\)
Từ đó ta có hệ phương trình
\(\left\{ \begin{array}{l}2b + c = – 1\\4a + 6b + c = – 13\\8a + 2b + c = – 17\end{array} \right.\)
Dùng máy tính cầm tay giải HPT, ta được \(a = – 2,{\rm{ }}b = – 1,{\rm{ }}c = 1.\)
Vậy phương trình đường tròn cần tìm là: \({x^2} + {y^2} -4x -2y + 1 = 0\)
Giải bài 1.19 trang 23 Chuyên đề học tập Toán 10
Một đoàn xe chở 255 tấn gạo tiếp tế cho đồng bào vùng bị lũ lụt. Đoàn xe có 36 chiếc gồm ba loại: xe chở 5 tấn, xe chở 7 tấn và xe chở 10 tấn. Biết rằng tổng số hai loại xe chở 5 tấn và chở 7 tấn nhiều gấp ba lần số xe chở 10 tấn. Hỏi mỗi loại xe có bao nhiêu chiếc?
Lời giải chi tiết
Gọi số xe mỗi loại lần lượt là x,y,z (\(x,y,z \in \mathbb{N}\))
Có tổng 36 chiếc nên \(x + y + z = 36\)
Cả đoàn chở được 255 tấn gạo nên ta có: \(5x + 7y + 10z = 255\)
Tổng số hai loại xe chở 5 tấn và chở 7 tấn nhiều gấp ba lần số xe chở 10 tấn nên ta có: \(x + y = 3z\) hay \(x + y – 3z = 0\)
Từ đó ta có hệ phương trình
\(\left\{ \begin{array}{l}x + y + z = 36\\5x + 7y + 10z = 255\\x + y – 3z = 0\end{array} \right.\)
Dùng máy tính cầm tay giải HPT, ta được \(x = 12,y = 15,z = 9.\)
Vậy có 12 xe loại 5 tấn, 15 xe loại 7 tấn và 9 xe loại 10 tấn.
Giải bài 1.20 trang 23 Chuyên đề học tập Toán 10
Bác An là chủ cửa hàng kinh doanh cà phê cho những người sành cà phê. Bác có ba loại cà phê nổi tiếng của Việt Nam: Aribica, Robusta và Moka với giá bán lần lượt là 320 nghìn đồng/kg, 280 nghìn đồng/kg và 260 nghìn đồng/kg. Bác muốn trộn ba loại cà phê này để được một hỗn hợp cà phê, sau đó đóng thành các gói 1kg, bán với giá 300 nghìn đồng/kg và lượng cà phê Moka gấp đôi lượng cà phê Robusta trong mỗi gói. Hỏi bác cần trộn ba loại cà phê này theo tỉ lệ nào?
Lời giải chi tiết
Gọi số kg mỗi loại cà phê Aribica, Robusta và Moka trong 1kg hỗn hợp mới là x:y:z (kg) (\(x,y,z \ge 0\))
Dễ thấy: \(x + y + z = 1\)
Giá bán của hỗn hợp cà phê thu được là 300 nghìn đồng nên ta có: \(320x + 280y + 260z = 300\)
Lượng cà phê Moka gấp đôi lượng cà phê Robusta trong mỗi gói nên: \(z = 2y\)
Từ đó ta có hệ phương trình:
\(\left\{ \begin{array}{l}x + y + z = 1\\320x + 280y + 260z = 300\\2y – z = 0\end{array} \right.\)
Dùng máy tính cầm tay giải hệ phương trình ta được \(x = \frac{5}{8},y = \frac{1}{8},z = \frac{1}{4}.\)
Vậy tỉ lệ trộn ba loại Aribica, Robusta và Moka là 5:1:2.
Giải bài 1.21 trang 23 Chuyên đề học tập Toán 10
Bác Việt có 12 ha đất canh tác để trồng ba loại cây: ngô, khoai tây và đậu tương. Chi phí trồng 1 ha ngô là 4 triệu đồng, 1 ha khoai tây là 3 triệu đồng và 1 ha đậu tương là 4,5 triệu đồng. Do nhu cầu thị trường, bác đã trồng khoai tây trên phần diện tích gấp đôi diện tích trồng ngô. Tổng chi phí trồng ba loại cây trên là 45,25 triệu đồng. Hỏi diện tích trồng mỗi loại cây là bao nhiêu?
Lời giải chi tiết
Gọi số ha trồng ngô, khoai tây và đậu tương là x:y:z (ha) (\(x,y,z > 0\))
Bác Việt có 12 ha đất canh tác để trồng nên ta có: \(x + y + z = 12\)
Bác đã trồng khoai tây trên phần diện tích gấp đôi diện tích trồng ngô hay \(y = 2x\)
Tổng chi phí là 45,25 triệu đồng nên: \(4x + 3y + 4,5z = 45,25\)
Từ đó ta có hệ phương trình:
\(\left\{ \begin{array}{l}x + y + z = 12\\2x – y = 0\\4x + 3y + 4,5z = 45,25\end{array} \right.\)
Dùng máy tính cầm tay giải hệ phương trình ta được \(x = 2,5;y = 5;z = 4,5.\)
Vậy bác đã trồng 2,5 ha ngô, 5 ha khoai tây và 4,5 ha đậu tương.
Giải bài 1.22 trang 24 Chuyên đề học tập Toán 10
Cân bằng phương trình phản ứng hóa học sau:
\(Fe{S_2} + {O_2} \to F{e_2}{O_3} + S{O_2}\)
Lời giải chi tiết
Giả sử x, y, z, t là bốn số nguyên dương thỏa mãn cân bằng phản ứng
\(xFe{S_2} + y{O_2} \to zF{e_2}{O_3} + tS{O_2}\)
Vì số nguyên tử iron, sulfur và oxygen ở hai vế phải bằng nhau nên ta có hệ
\(\left\{ \begin{array}{l}x = 2z\\2x = t\\2y = 3z + 2t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{x}{t} = 2\frac{z}{t}\\2\frac{x}{t} = 1\\2\frac{y}{t} = 3\frac{z}{t} + 2\end{array} \right.\)
Đặt \(X = \frac{x}{t};Y = \frac{y}{t};Z = \frac{z}{t}\) ta được hệ phương trình bậc nhất ba ẩn
\(\left\{ \begin{array}{l}X = 2Z\\2X = 1\\2Y = 3Z + 2\end{array} \right.\) hay \(\left\{ \begin{array}{l}X – 2Z = 0\\2X = 1\\2Y – 3Z = 2\end{array} \right.\)
Dùng máy tính cầm tay giải hệ sau cùng ta được \(X = \frac{1}{2},Y = \frac{{11}}{8},Z = \frac{1}{4}\). Từ đây suy ra \(22x = 8y = 44z = 11t\). Chọn \(y = 11\) ta được \(x = 4,z = 2,t = 8\).
Từ đó ta được phương trình cân bằng
\(4Fe{S_2} + 11{O_2} \to 2F{e_2}{O_3} + 8S{O_2}\)
Giải bài 1.23 trang 24 Chuyên đề học tập Toán 10
Bạn Mai có ba lọ dung dịch chứa một loại acid. Dung dịch A chứa 10%, dung dịch B chứa 30% và dung dịch C chứa 50% acid. Bạn Mai lấy từ mỗi lọ một lượng dung dịch và hòa với nhau để có 50g hỗn hợp chứa 32% acid này và lượng dung dịch loại C lấy nhiều gấp đôi dung dịch loại A. Tính lượng dung dịch mỗi loại bạn Mai đã lấy.
Lời giải chi tiết
Gọi lượng dung dịch A, B, C Mai đã lấy lần lượt là x, y, z (g) (\(x,y,z \ge 0\))
Khi hòa với nhau thu được 50g hỗn hợp mới nên ta có: \(x + y + z = 50\)
Phần trăm lượng acid trong dung dịch mới là: \(10x + 30y + 50z = 32.50\)
Lượng dung dịch loại C lấy nhiều gấp đôi dung dịch loại A hay \(z = 2x\)
Từ đó ta có hệ phương trình bậc nhất ba ẩn \(\left\{ \begin{array}{l}x + y + z = 50\\10x + 30y + 50z = 32.50\\2x – z = 0\end{array} \right.\)
Dùng máy tính cầm tay, giải hpt ta được \(x = 5,y = 35,z = 10\)
Vậy Mai cần hòa 5g dung dịch A cùng 35g dung dịch B với 10g dung dịch C.
Giải bài 1.24 trang 24 Chuyên đề học tập Toán 10
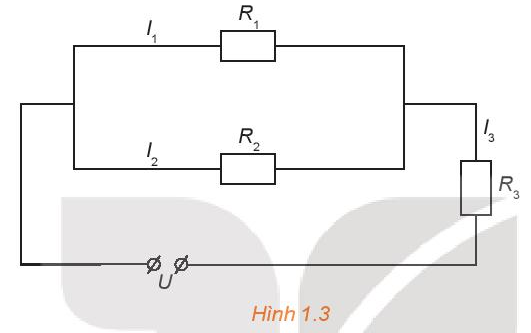
Cho đoạn mạch như Hình 1.3. Biết \({R_1} = 36\Omega ,{\rm{ }}{R_2} = 45\Omega ,{I_3} = 1,5A\) là cường độ dòng điện trong mạch chính và hiệu điện thế giữa hai đầu đoạn mạch U = 60V. Gọi \({I_1}\) và \({I_2}\) là cường độ dòng diện trong mạch rẽ. Tính \({I_1},{I_2}\)và \({R_3}.\)
Lời giải chi tiết
Với mạch nối tiếp: \({I_1} = {I_2} = {I_3} = …{I_n}\), \(U = {U_1} + {U_2} + {U_3} + …{U_n}\).
Với mạch song song: \({U_1} = {U_2} = {U_3} = …{U_n}\), \(I = {I_1} + {I_2} + {I_3} + … + {I_n}\).
Từ sơ đồ mạch điện, ta có:
\(\left\{ \begin{array}{l}{I_3} = {I_1} + {I_2}\\{I_1}.{R_1} + {I_3}.{R_3} = U\\{I_1}.{R_1} = {I_2}.{R_2}\end{array} \right.\)
hay \(\left\{ \begin{array}{l}{I_1} + {I_2} = 1,5\\{I_1}.36 + 1,5.{R_3} = 60\\{I_1}.36 = {I_2}.45\end{array} \right.\)
Vậy \({I_1} = \frac{5}{{6}};{I_2} = \frac{2}{3};{R_3} = 20\Omega .\)
Giải bài 1.24 trang 24 Chuyên đề học tập Toán 10
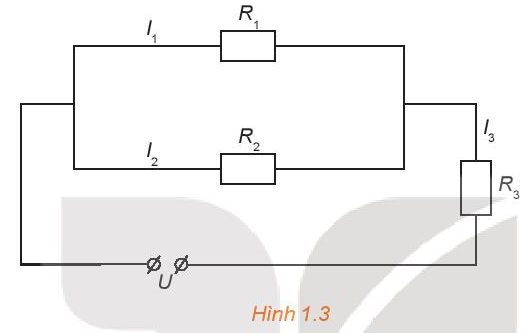
Cho đoạn mạch như Hình 1.3. Biết \({R_1} = 36\Omega ,{\rm{ }}{R_2} = 45\Omega ,{I_3} = 1,5A\) là cường độ dòng điện trong mạch chính và hiệu điện thế giữa hai đầu đoạn mạch U = 60V. Gọi \({I_1}\) và \({I_2}\) là cường độ dòng diện trong mạch rẽ. Tính \({I_1},{I_2}\)và \({R_3}.\)
Lời giải chi tiết
Với mạch nối tiếp: \({I_1} = {I_2} = {I_3} = …{I_n}\), \(U = {U_1} + {U_2} + {U_3} + …{U_n}\).
Với mạch song song: \({U_1} = {U_2} = {U_3} = …{U_n}\), \(I = {I_1} + {I_2} + {I_3} + … + {I_n}\).
Từ sơ đồ mạch điện, ta có:
\(\left\{ \begin{array}{l}{I_3} = {I_1} + {I_2}\\{I_1}.{R_1} + {I_3}.{R_3} = U\\{I_1}.{R_1} = {I_2}.{R_2}\end{array} \right.\)
hay \(\left\{ \begin{array}{l}{I_1} + {I_2} = 1,5\\{I_1}.36 + 1,5.{R_3} = 60\\{I_1}.36 = {I_2}.45\end{array} \right.\)
Vậy \({I_1} = \frac{5}{{6}};{I_2} = \frac{2}{3};{R_3} = 20\Omega .\)
Giải bài 1.25 trang 24 Chuyên đề học tập Toán 10
Giải bài toán dân gian sau:
Em đi chợ phiên
Anh gửi một tiền
Cam, thanh yên, quýt
Không nhiều thỉ ít
Mua đủ một trǎm
Cam ba đồng một
Quýt một đồng năm
Thanh yên tươi tôt
Năm đồng một trái.
Hỏi mỗi thứ mua bao nhiêu trái, biết một tiển bằng 60 đồng?
Lời giải chi tiết
Gọi số quả Cam, thanh yên, quýt lần lượt là x, y, z (\(x,y,z \in \mathbb{N}*\))
“Mua đủ một trǎm” tức là \(x + y + z = 100\)
“Cam ba đồng một” => giá một quả cam là 3 đồng
“Quýt một đồng năm” => giá một quả quýt là \(\frac{1}{5} = 0,2\) đồng
Thanh yên giá 5 đồng/quả.
Tổng số tiền là 1 tiền = 60 đồng nên ta có: \(3x + 0,2y + 5z = 60\)
Ta có hệ phương trình
\(\left\{ \begin{array}{l}x + y + z = 100\\3x + 0,2y + 5z = 60\end{array} \right.\)
Nhân phương trình thứ nhất với 3 rồi trừ đi phương trình thứ 2 theo từng vế tương ứng ta được
\(\left\{ \begin{array}{l}x + y + z = 100\\2,8y – 2z = 240\end{array} \right.\) hay \(\left\{ \begin{array}{l}x + y + z = 100\\1,4y – z = 120\end{array} \right.\)
Từ phương trình thứ hai ta có: \(z = 1,4y – 120\)
Thay vào phương trình thứ nhất ta được \(x = 220 – 2,4y\)
Vì \(x,y,z \in \mathbb{N}*\) nên \(y \vdots 10\) và \(\left\{ \begin{array}{l}1,4y – 120 > 0\\220 – 2,4y > 0\end{array} \right.\)
\( \Leftrightarrow \) \(y \vdots 10\) và \(\frac{{120}}{{1,4}} < y < \frac{{220}}{{2,4}}\) hay \(86 \le y \le 91\).
Do đó \(y = 90 \Rightarrow x = 4,z = 6\)
Vậy người đó đã mua 4 quả cam, 90 quả quýt và 6 quả thanh yên.
Giải bài 1.26 trang 24 Chuyên đề học tập Toán 10
Một con ngựa giá 204 đồng (đơn vị tiền cổ). Có ba người muốn mua nhung mỗi người không đủ tiển mua. Người thứ nhất nói với hai người kia: “Mỗi anh cho tôi vay một nửa số tiền của mình thì tôi đủ tiền mua ngựa”; Người thứ hai nói: “Mỗi anh cho tôi vay một phần ba số tiền của mỉnh, tôi sẽ mua được ngựa”; Người thú ba lại nói: “Chỉ cần mỗi anh cho tôi vay một phần tư số tiền của mình thi con ngựa sẽ là của tôi”. Hỏi mỗi người có bao nhiêu tiển?
Lời giải chi tiết
Gọi số tiền mỗi người có lần lượt là x, y, z (đồng) (\(x,y,z \ge 0\))
Người thứ nhất nói với hai người kia: “Mỗi anh cho tôi vay một nửa số tiền của mình thì tôi đủ tiền mua ngựa” tức là: \(x + \frac{1}{2}y + \frac{1}{2}z = 204\)
Người thứ hai nói: “Mỗi anh cho tôi vay một phần ba số tiền của mỉnh, tôi sẽ mua được ngựa” tức là: \(\frac{1}{3}x + y + \frac{1}{3}z = 204\)
Người thứ ba lại nói: “Chỉ cần mỗi anh cho tôi vay một phần tư số tiền của mình thi con ngựa sẽ là của tôi” tức là: \(\frac{1}{4}x + \frac{1}{4}y + z = 204\)
Từ đó ta có hệ phương trình bậc nhất ba ẩn \(\left\{ \begin{array}{l}x + \frac{1}{2}y + \frac{1}{2}z = 204\\\frac{1}{3}x + y + \frac{1}{3}z = 204\\\frac{1}{4}x + \frac{1}{4}y + z = 204\end{array} \right.\)
Dùng máy tính cầm tay, giải hpt ta được \(x = 60,y = 132,z = 156\)
Vậy người thứ nhất có 60 đồng, người thứ hai có 132 đồng và người thứ ba có 156 đồng.
