Toán 11 tập 1 trang 104 Bài 3: Đường thẳng và mặt phẳng song song

Giải toán 11 tập 1 trang 104 Bài 3 sách Cánh diều có đáp án chi tiết cho từng Bài trong sách giáo khoa Toán lớp 11 Cánh diều. Mời các em học sinh cùng quý phụ huynh tham khảo.

Trang 101 toán 11 tập 1

Hoạt động 1 trang 101 toán 11 tập 1

a) Trong Hình 44, thanh barrier và mặt đường gợi nên hình ảnh đường thẳng d và mặt phẳng (P).Cho biết đường thẳng d và mặt phẳng (P) có điểm chung hay không.

b) Cho đường thẳng d và mặt phẳng (P). Hãy cho biết các khả năng có thể xảy ra đối với số điểm chung của d và (P).

Lời giải:

a) Đường thẳng d và mặt phẳng (P) không có điểm chung

b) Có ba khả năng có thể xảy ra đối với số điểm chung của d và (P):

– d và (P) có từ hai điểm chung trở lên khi d nằm trong (P)

– d và (P) có một điểm chung duy nhất khi d và (P) cắt nhau

– d và (P) không có điểm chung khi d song song với (P)

Trang 102 toán 11 tập 1

Luyện tập 1 trang 102 toán 11 tập 1

Quan sát các xà ngang trên sân tập thể dục ở Hình 47. Hãy cho biết vị trí tương đối của các xà ngang đó với mặt sân.

Lời giải:

Các xà ngang song song với mặt sân

HĐ 2 trang 102 toán 11 tập 1

Cho đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) (Hình 48). Gọi (Q) là mặt phẳng xác định bởi hai đường thẳng song song a, a’.

a) Giả sử a cắt (P) tại M. Đường thẳng a có cắt đường thẳng a’ tại M hay không?

b) Nêu vị trí tương đối của đường thẳng a và mặt phẳng (P). Vì sao?

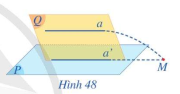
Lời giải:

a) Đường thẳng a không cắt đường thẳng a’ tại M

b) Đường thẳng a và mặt phẳng (P) song song với nhau vì chúng không có điểm chung

LT 2 trang 102 toán 11 tập 1

Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, AD. Các đường thẳng MN, NP, PM có song song với mặt phẳng (BCD) không? Vì sao?

Lời giải:

Tam giác ABC có: M, N là trung điểm của AB, AC

Suy ra MN // BC nên MN // (BCD)

Tam giác ACD có: N, P là trung điểm của AC, AD

Suy ra NP // CD nên NP // (BCD)

Tam giác ABD có: M, P là trung điểm của AB, AD

Suy ra MP // BD nên MP // (BCD)

HĐ 3 trang 102 toán 11 tập 1

Cho đường thẳng a song song với mặt phẳng (P). Cho mặt phẳng (Q) chứa a và cắt (P) theo giao tuyển b. (Hình 51)

a) Giả sử a cắt b tại M. Đường thẳng a có cắt mặt phẳng (P) tại M hay không?

b) Nêu vị trí tương đối của hai đường thẳng a và b. Vì sao?

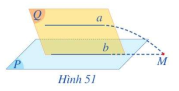
Lời giải:

a) Đường thẳng a không cắt mặt phẳng (P) tại M

b) Hai đường thẳng a và b song song với nhau

Trang 103 toán 11 tập 1

LT 3 trang 103 toán 11 tập 1

Ở Ví dụ 3, xác định giao tuyến của mặt phẳng (R) với các mặt phẳng (ABD), (BCD), (ACD).

Lời giải:

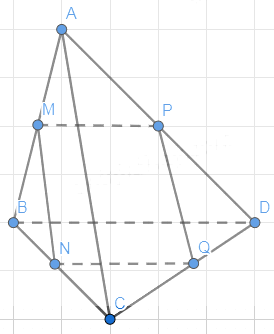
Ta có: M là giao điểm của (R) và (ABD)

Mà (R) // BD

Từ M kẻ MP // BD và cắt AD tại P

Suy ra MP là giao tuyến của (R) và (ABD)

Từ M kẻ MN // AC, cắt BC tại N

Do đó, N là giao điểm của (R) và (BCD)

Từ N kẻ Nx // BD, cắt CD tại Q

Suy ra NQ là giao tuyển của (R) và (BCD)

Ta có P là giao điểm của (R) và (ACD)

Từ P kẻ PH // AC, cắt CD tại H

Suy ra PH là giao tuyến của (R) và (ACD)

HĐ 4 trang 103 toán 11 tập 1

Cho hai mặt phẳng (P), (Q) cùng song song với đường thẳng a và (P) ∩ (Q) = b (Hình 54).

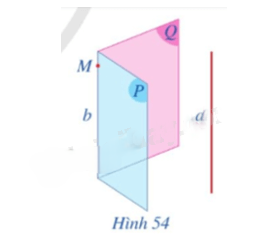
a) Lấy một điểm M trên đường thẳng b. Gọi b’, b” lần lượt là các giao tuyến của mặt phẳng (M, a) với (P) và mặt phẳng (M, a) với (Q). Cho biết b’ và b” có trùng với b hay không.

b) Nêu vị trí tương đối của hai đường thẳng a và b. Vì sao?

Lời giải:

a) • Ta có: M ∈ b và (P) ∩ (Q) = b;

Suy ra M ∈ (P).

Mà M ∈ (M, a)

Do đó M là giao điểm của (P) và (M, a).

Lại có b’ = (P) ∩ (M, a)

Suy ra đường thẳng b’ đi qua M.

Tương tự ta cũng chứng minh được b’’ đi qua điểm M.

• Ta có: a // (P);

a ⊂ (M, a)

(M, a) ∩ (P) = b’

Do đó a // b’.

Tương tự ta cũng có a // b’’.

Do đó b’ // b’’.

Mặt khác: (P) ∩ (Q) = b;

(M, a) ∩ (P) = b’;

(M, a) ∩ (Q) = b’’;

b // b’’.

Do đó b // b’ // b’’.

Mà cả ba đường thẳng cùng đi qua điểm M nên ba đường thẳng này trùng nhau.

b) Vì a // b’ nên a // b (do b ≡ b’).

Trang 104 toán 11 tập 1

LT 4 trang 104 toán 11 tập 1

Trong Hình 56, hai mặt tường của căn phòng gợi nên hình ảnh hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến b, mép cột gợi nên hình ảnh đường thẳng a. Cho biết đường thẳng a có song song với giao tuyến b hay không.

Lời giải:

Đường thẳng a song song với giao tuyến b

Bài 1 trang 104 sgk Toán 11 tập 1 Cánh diều

Trong phòng học của lớp, hãy nêu những hình ảnh về đường thẳng song song với mặt phẳng.

Bài giải:

Những hình ảnh về đường thẳng song song với mặt phẳng: mép cột dọc với bảng; xà ngang trần nhà với mặt sàn; …

Bài 2 trang 104 sgk Toán 11 tập 1 Cánh diều

Trong Hình 57, khi cắt bánh sinh nhật, mặt cắt và mặt khay đựng bánh lần lượt gợi nên hình ảnh mặt phẳng (Q) và mặt phẳng (P); mép trên và mép dưới lát cắt lần lượt gợi nên hình ảnh hai đường thẳng a và b trong đó a song song với mặt phẳng (P). Cho biết hai đường thẳng a, b có song song với nhau hay không.

Bài giải:

Hai đường thẳng a, b có song song với nhau vì a song song với (P) mà (Q) cắt (P) tại giao tuyến b.

Bài 3 trang 104 sgk Toán 11 tập 1 Cánh diều

Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABD, điểm I nằm trên cạnh BC sao cho BI = 2IC. Chứng minh rằng IG song song với mặt phẳng (ACD).

Bài giải:

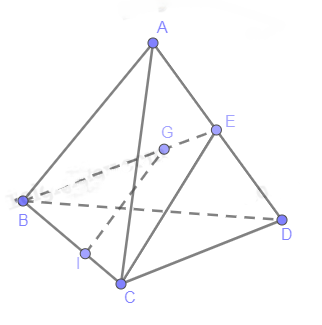
Tam giác BCE có E là trung điểm AD

Suy ra:$\frac{{BG}}{{BE}} = \frac{{BI}}{{BC}} = \frac{2}{3}$

Theo Ta lét, IG //CE

Mà CE thuộc (ACD)

Suy ra: IG // (ACD)

Bài 4 trang 104 sgk Toán 11 tập 1 Cánh diều

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng đường thẳng MN song song với giao tuyến d của hai mặt phẳng (SBC) và (SAD).

Bài giải:

Lời giải

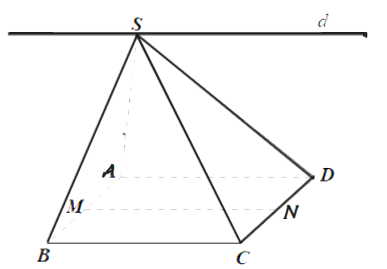
Ta có: S ∈ (SAD) và S ∈ (SBC) nên S là giao điểm của (SAD) và (SBC).

Lại có: AD // BC (do ABCD là hình bình hành);

AD ⊂ (SAD);

BC ⊂ (SBC).

Do đó giao tuyến d của hai mặt phẳng (SAD) và (SBC) là đường thẳng đi qua S và song song với AD, BC.

Vì M, N lần lượt là trung điểm của AB và CD nên MN là đường trung bình

Do đó MN // BC // AD.

Ta có: MN // BC mà BC ⊂ (SBC) nên MN // (SBC);

MN // AD mà AD ⊂ (SAD) nên MN // (SAD).

Có: MN // (SBC);

MN // (SAD);

(SAD) ∩ (SBC) = d

Suy ra MN // d.

Bài 5 trang 104 sgk Toán 11 tập 1 Cánh diều

Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi M, N lần lượt là trọng tâm của hai tam giác ABF và ABC. Chứng minh rằng đường thẳng MN song song với mặt phẳng (ACF).

Bài giải:

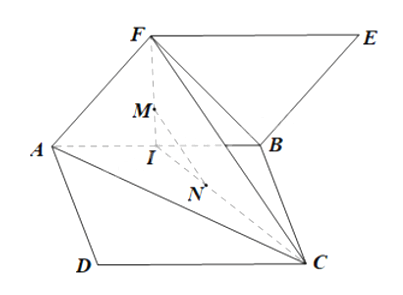
Gọi I là trung điểm của AB.

M là trọng tâm tam giác ABF suy ra $\frac{{IM}}{{IF}} = \frac{1}{3}$.

N là trọng tâm tam giác ABC suy ra $\frac{{IN}}{{IC}} = \frac{1}{3}$.

Xét tam giác ICF có $\frac{{IM}}{{IF}} = \frac{{IN}}{{IC}} = \frac{1}{3}$ suy ra MN//FC (định lí Thales đảo).

Mà FC thuộc mặt phẳng (AFC) suy ra MN//(AFC).

Bài 6 trang 104 sgk Toán 11 tập 1 Cánh diều

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Lấy điểm M trên cạnh AD sao cho AD = 3AM. Gọi G, N lần lượt là trọng tâm của tam giác SAB, ABC.

a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD).

b) Chứng minh rằng MN song song với mặt phẳng (SCD) và NG song song với mặt phẳng (SAC).

Bài giải:

a) S là điểm chung của hai mặt phẳng (SAB) và (SCD) mà AB // CD

Từ S kẻ Sx sao cho Sx // AB // CD nên Sx là giao tuyến của hai mặt phẳng (SAB) và (SCD).

b) Gọi I, K là trung điểm của BC, AC

mà hai đường chéo của hình bình hành cắt nhau tại trung điểm mỗi đường

Suy ra K là trung điểm của BD

$\triangle$DAB có: $\frac{DN}{DB}=\frac{DK+KN}{DB}=\frac{\frac{1}{2}DB+\frac{1}{6}DB}{DB}=\frac{2}{3}=\frac{DM}{DA}$

Suy ra: MN // AB mà AB // CD

Do đó: MN // CD nên MN // (SCD).

Gọi E là trung điểm của AB

G là trọng tâm $\triangle$SAB nên $\frac{EG}{SE}=\frac{1}{3}$

N là trọng tâm $\triangle$ABC nên $\frac{EN}{EC}=\frac{1}{3}$

$\triangle$ESC có: $\frac{EG}{SE}=\frac{EN}{EC}$ suy ra GN // SC

mà SC thuộc (SAC). Do đó: GN // (SAC).