Giải Toán 11 tập 1 trang 12 bài 1: Góc lượng giác
Giải Toán 11 tập 1 trang 12 bài 1: Góc lượng giác
Giải toán 11 tập 1 trang 12 Bài 1 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 11 Chân trời sáng tạo. Mời các em học sinh cùng quý phụ huynh tham khảo.
Giải Toán 11 tập 1 trang 7
Hoạt động 1 trang 7 Toán 11 tập 1
Một chiếc bánh lái tàu có thể quay theo cả hai chiều. Trong Hình 1 và Hình 2, lúc đầu thanh OM ở vị trí OA.
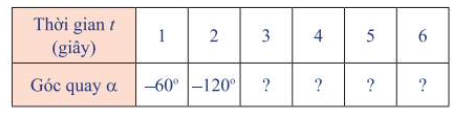
a) Khi quay bánh lái ngược chiều kim đồng hồ ( Hình 1), cứ mỗi giây, bánh lái quay một góc $ {60^0}$. Bảng dưới đây cho ta góc quay $\alpha $của thanh OM sau t giây kể từ lúc bắt đầu quay. Thay dấu ? bằng số đo thích hơp.
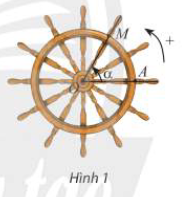

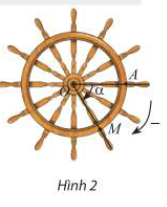
b) Nếu bánh lái được quay theo chiều ngược lại, nghĩa là quay cùng chiều kim đồng hồ ( Hình 2) với cùng tốc độ như trên, người ta ghi -${60^ \circ }$để chỉ góc mà thanh OM quay được sau mỗi giây. Bảng dưới đây cho ta góc quay $\alpha $của thanh OM sau t giây kể từ lúc bắt đầu quay. Thay dấu ? bằng số đo thích hợp.
Lời giải:
a)
| Thời gian t (giây) | 1 | 2 | 3 | 4 | 5 | 6 |
| Góc quay $\alpha $ | ${60^ \circ }$ | ${120^ \circ }$ | ${180^ \circ }$ | ${240^ \circ }$ | ${300^ \circ }$ | ${360^ \circ }$ |
b)
| Thời gian t (giây) | 1 | 2 | 3 | 4 | 5 | 6 |
| Góc quay $\alpha $ | -${60^ \circ }$ | -${120^ \circ }$ | -${180^ \circ }$ | -${240^ \circ }$ | -${300^ \circ }$ | -${360^ \circ }$ |
Giải Toán 11 tập 1 trang 9
Thực hành 1 trang 9 Toán 11 tập 1
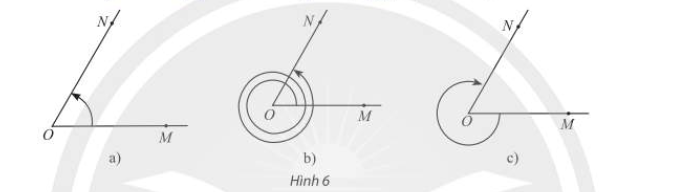
Cho $\widehat {MON} = {60^ \circ }$. Xác định số đo của các góc lượng giác được biểu diễn trong Hình 6 và viết công thức tổng quát của số đo góc lượng giác (OM,ON).
Lời giải:
a) Số đo của góc lượng giác (OM,ON) trong Hình 6 là ${60^ \circ }$
b) Số đo của góc lượng giác (OM,ON) trong Hình 6 là ${60^ \circ } + {2.360^ \circ } = {780^ \circ }$
c) Số đo của góc lượng giác (OM,ON) trong Hình 6 là $\frac{5}{6}.( – {360^ \circ }) = – {300^ \circ }$
Công thức tổng quát của số đo góc lượng giác $(OM,ON) = {60^ \circ } + k{360^ \circ }(k \in \mathbb{Z})$
Vận dụng 1 trang 9 Toán 11 tập 1
Trong khoảng thời gian từ 0 giờ đến 2 giờ 15 phút, kim phút quét một góc lượng giác là bao nhiêu độ?
Lời giải:
Đổi 2 giờ 15 phút = $\frac{9}{4}$giờ.
Trong khoảng thời gian từ 0 giờ đến 2 giờ 15 phút, kim phút quét một góc lượng giác là $\frac{9}{4}.( – {360^ \circ }) = – {810^ \circ }$
Hoạt động 2 trang 9 Toán 11 tập 1
Cho Hình 7.
a) Xác định số đo các góc lượng giác (Oa,Ob), (Ob,Oc) và (Oa,Oc).
b) Nhận xét về mối liên hệ giữa ba số đo góc này.
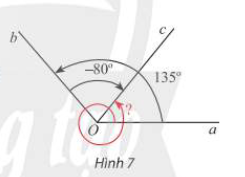
Lời giải:
a) Số đo của góc lượng giác (Oa,Ob) trong Hình 7 là ${135^ \circ } + n{.360^ \circ },(n \in \mathbb{Z})$
Số đo của góc lượng giác (Ob,Oc) trong Hình 7 là $ – {80^ \circ } + m{.360^ \circ },(m \in \mathbb{Z})$
Số đo của góc lượng giác (Oa,Oc) trong Hình 7 là ${415^ \circ } + k{.360^ \circ },(k \in \mathbb{Z})$
b)
$\begin{array}{l}(Oa,Ob) + (Ob,Oc) = {135^ \circ } + n{.360^ \circ } + ( – {80^ \circ }) + m{.360^ \circ }\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {55^ \circ } + (n + m){.360^ \circ } = {415^ \circ } + (n + m – 1){.360^ \circ }\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {415^ \circ } + k{.360^ \circ } = (Oa,Oc)\end{array}$
với $k = n + m – 1\,;n,m,k \in \mathbb{Z}$
Vận dụng 2 trang 9 Toán 11 tập 1
Trong Hình 8, chiếc quạt có ba cánh được phân bố đều nhau. Viết công thức tổng quát số đo của góc lượng giác (Ox,ON) và (Ox,OP).
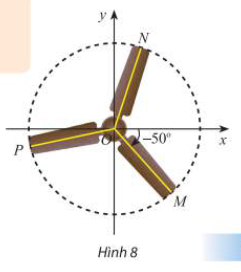
Lời giải:
Công thức tổng quát số đo của góc lượng giác $(Ox,ON) = {70^ \circ } + k{360^ \circ }(k \in \mathbb{Z})$
Công thức tổng quát số đo của góc lượng giác $(Ox,OP) = (Ox,OM) + (OM,OP) = – {50^ \circ } + ( – {120^ \circ }) + m{360^ \circ } = – {170^ \circ } + m{360^ \circ }\,\,\,\,,(m \in \mathbb{Z})$
Giải Toán 11 tập 1 trang 10
Hoạt động 3 trang 10 Toán 11 tập 1
Vẽ đường tròn tâm O bán kính R bất kì. Dùng một đoạn dây mềm đo bán kính và đánh dấu được một cung AB có độ dài đúng bằng R (Hình 9). Đo và cho biết $\widehat {AOB}$ có số đo bằng bao nhiêu độ.
Lời giải:
$ \Rightarrow \widehat {AOB} = 60^\circ $
Giải Toán 11 tập 1 trang 11
Thực hành 2 trang 11 Toán 11 tập 1
Hoàn thành bảng chuyển đổi đơn vị đo của các góc sau đây:
| Số đo theo độ | 0° | ? | 45° | 60° | ? | 120° | ? | 150° | 180° |
| Số đo theo rad | ? | $\frac{\pi }{6}(rad)$ | ? | ? | $\frac{\pi }{2}(rad)$ | ? | $\frac{{3\pi }}{4}(rad)$ | ? | $\pi (rad)$ |
Lời giải:
| Số đo theo độ | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° |
| Số đo theo rad | 0 | $\frac{\pi }{6}(rad)$ | $\frac{\pi }{4}\left( {rad} \right)$ | $\frac{\pi }{3}\left( {rad} \right)$ | $\frac{\pi }{2}(rad)$ | \[\frac{{2\pi }}{3}(rad)\] | $\frac{{3\pi }}{4}(rad)$ | $\frac{{5\pi }}{6}(rad)$ | $\pi (rad)$ |
Hoạt động 4 trang 11 Toán 11 tập 1
Trong mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O bán kính bằng 1 và điểm A(1; 0).
a) Cho điểm B(0; 1). Số đo góc lượng giác (OA; OB) bằng bao nhiêu radian?
b) Xác định các điểm A’ và B’ trên đường tròn sao cho các góc lượng giác (OA; OA’), (OA, OB’) có số đo lần lượt là $\pi \,$ và $ – \frac{\pi }{2}$
Lời giải:
a)
Góc lượng giác $\left( {OA;OB} \right) = 90^\circ = \frac{\pi }{2}$
b)
Học sinh vẽ hình theo yêu cầu
Giải Toán 11 tập 1 trang 12
Thực hành 3 trang 12 Toán 11 tập 1
Biểu diễn trên đường tròn lượng giác các góc lượng giác có số đo là:
a) $ – {1485^ \circ }$
b) $\frac{{19\pi }}{4}$
Lời giải:
a) Ta có $ – {1485^ \circ } = – {45^ \circ } + ( – 4){.360^ \circ }$. Vậy điểm biểu diễn góc lượng giác có số đo $ – {1485^ \circ }$là điểm M trên đường tròn lượng giác thuộc góc phần tư thứ IV sao cho $\widehat {AMO} = {45^ \circ }$
b) Ta có $\frac{{19\pi }}{4} = \frac{{3\pi }}{4} + 4\pi $. Vậy điểm biểu diễn góc lượng giác có số đo $\frac{{19\pi }}{4}$ là điểm N trên phần đường tròn lượng giác thuộc góc phần tư thứ II sao cho $\widehat {AMO} = \frac{{3\pi }}{4}$.
Giải bài 1 trang 12 Toán 11 tập 1
Đổi số đo của các góc sau đây sang radian:
a) 38o
b) -115o
c) ($\frac{3}{\pi }$)o
Lời giải
a) $38^{o} = \frac{19\pi }{90}$ rad
b) $-115^{o} = – \frac{23\pi }{36}$ rad
c) $\left ( \frac{3}{\pi } \right )^{o} = \frac{1}{60}$ rad
Giải bài 2 trang 12 Toán 11 tập 1
Đổi số đo của các góc sau đây sang độ:
a) $\frac{\pi }{12}$
b) -5
c) $\frac{13\pi }{9}$
Lời giải
$\frac{\pi }{12} = 15^{o}$
$-5 = – 286,5^{o}$
$\frac{13\pi }{9} = 260^{o}$
Giải bài 3 trang 12 Toán 11 tập 1
Biểu diễn các góc lượng giác sau trên đường tròn lượng giác
a) $\frac{-17\pi }{3}$
b) $\frac{13\pi }{4}$
c) $-765^{o}$
Lời giải
a) Ta có $\frac{-17\pi }{3} = \frac{\pi }{3} – 3.2\pi$. Vậy điểm biểu diễn góc lượng giác có số đo $\frac{-17\pi }{3}$ là điểm M trên phần đường tròn lượng giác thuộc góc phần tư thứ I sao cho $\widehat{AOM} = \frac{\pi }{3}$
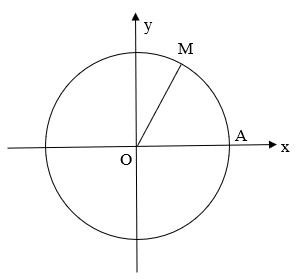
b) Ta có $\frac{13\pi }{4} = \frac{5\pi }{4} + 2\pi$. Vậy điểm biểu diễn góc lượng giác có số đo $\frac{13\pi }{4}$ là điểm N trên phần đường tròn lượng giác thuộc góc phần tư thứ III sao cho $\widehat{AON} = \frac{5\pi }{4}$
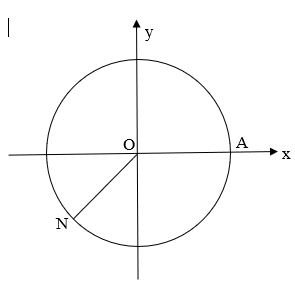
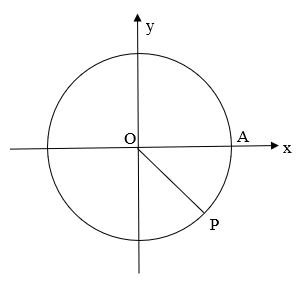
Ta có $-765^{o} = -45^{o} – 2.360^{o}$. Vậy điểm biểu diễn góc lượng giác có số đo $-765^{o}$ là điểm P trên phần đường tròn lượng giác thuộc góc phần tư thứ IV sao cho $\widehat{AOP} = -45^{o}$
Giải bài 4 trang 12 Toán 11 tập 1
Góc lượng giác $\frac{31\pi }{7}$ có cùng điểm biểu diễn trên đường tròn lượng giác với góc lượng giác nào sau đây?
$\frac{3\pi }{7} ; \frac{10\pi }{7} ; \frac{-25\pi }{7}$
Lời giải
Ta có:
$\frac{31\pi }{7} = \frac{3\pi }{7} + 2.2\pi$
$\frac{-25\pi }{7} = \frac{3\pi }{7} – 2.2\pi$
Vậy góc lượng giác $\frac{31\pi }{7}$ có cùng điểm biểu diễn với góc lượng giác $\frac{3\pi }{7} và \frac{-25\pi }{7}$
Giải bài 5 trang 12 Toán 11 tập 1
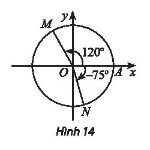
Viết công thức số đo tổng quát của các góc lượng giác (OA, OM) và (OA, ON) trong Hình 14
Lời giải
(OA, OM) = $\frac{2\pi }{3} + k.2\pi$
(OA, ON) = $\frac{5\pi }{12} + k.2\pi$
Giải bài 6 trang 12 Toán 11 tập 1
Viết công thức số đo tổng quát của góc lượng giác (Ox, ON).
Lời 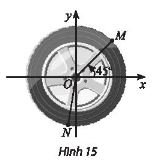 giải
giải
(Ox, ON) = −99o + k.360o
Giải Toán 11 tập 1 trang 13
Giải bài 7 trang 13 Toán 11 tập 1
Trên đường tròn lượng giác, hãy biểu diễn các góc lượng giác có số đo có dạng là:
a) $\frac{\pi }{2} + k\pi (k \epsilon \mathbb{Z})$
b) $k\frac{\pi }{4} (k \epsilon \mathbb{Z})$
Lời giải
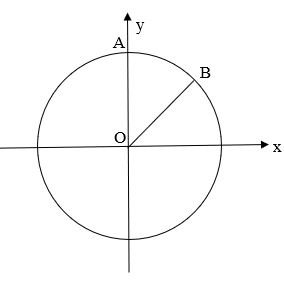
Góc lượng giác có số đo có dạng $\frac{\pi }{2} + k\pi (k\epsilon \mathbb{Z})$ được biểu diễn bằng điểm A trên đường tròn lượng giác.
Góc lượng giác có số đo có dạng $k\frac{\pi }{4} (k \epsilon \mathbb{Z})$ được biểu diễn bằng điểm B trên đường tròn lượng giác.
Giải bài 8 trang 13 Toán 11 tập 1
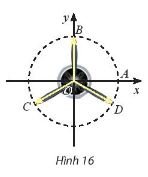
Vị trí các điểm B, C, D trên cánh quạt động cơ máy bay trong Hình 16 có thể được biểu diễn cho các góc lượng giác nào sau đây?
$\frac{\pi }{2} + k \frac{2\pi }{3} (k \epsilon \mathbb{Z}) ; \frac{-\pi }{6} + k \frac{2\pi }{3} (k \epsilon \mathbb{Z}) ; \frac{\pi }{3} + k \frac{\pi }{3} (k \epsilon \mathbb{Z})$
Lời giải
Điểm B, C, D biểu diễn cho góc lượng giác $\frac{\pi }{2} + k \frac{2\pi }{3} (k \epsilon \mathbb{Z})$
Giải bài 9 trang 13 Toán 11 tập 1
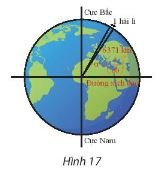
Hải li là một đơn vị chiều dài hàng hải, được tính bằng độ dài một cung chắn một góc α = ($\frac{1}{60}$)o của đường kinh tuyến (Hình 17). Đổi số đo α sang radian và cho biết 1 hải li bằng khoảng bao nhiêu kilômét, biết bán kính trung bình của Trái Đất là 6371km. Làm tròn kết quả đến hàng phần trăm.
Lời giải
$\alpha = \left ( \frac{1}{60}\right )^{o} = \frac{\pi }{10800}$ rad
1 hải li = $\frac{\pi }{10800} . 6371 \approx 1,85$ (km)
