Giải Toán 11 tập 1 trang 126 Bài 5: Phép chiếu song song
Giải Toán 11 tập 1 trang 126 Bài 5: Phép chiếu song song
Giải toán 11 tập 1 trang 126 Bài 5 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 11 Chân trời sáng tạo. Mời các em học sinh cùng quý phụ huynh tham khảo.
Giải Toán 11 tập 1 trang 121
Hoạt động 1 trang 121 Toán 11 tập 1
Trong hoạt động mở đầu:
a) Các tia sáng $AA’,BB’,DD’$ có song song với nhau hay không?
b) Nêu cách xác định bóng $C’$ của điểm $C$ trên mặt đường.
Lời giải:
a) $AA’\parallel BB’\parallel DD’$ vì cùng song song với đường thẳng $l$.
b) Cách xác định bóng $C’$ của điểm $C$ trên mặt đường:
‒ Qua $C$ dựng đường thẳng $d$ song song với đường thẳng $l$.
‒ Giao điểm của đường thẳng $d$ với mặt đường chính là bóng $C’$ của điểm $C$.
Giải Toán 11 tập 1 trang 122
Thực hành 1 trang 122 Toán 11 tập 1
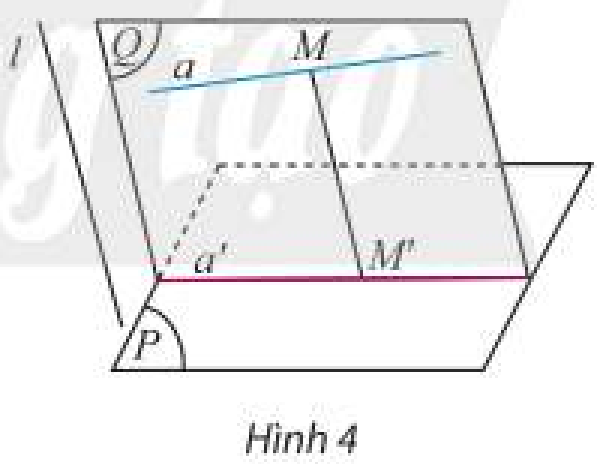
Tìm phương chiếu, mặt phẳng chiếu của phép chiếu song song được mô tả trong Hình 2.
Lời giải:
Phương chiếu: đường thẳng $a$.
Mặt phẳng chiếu: Mặt phẳng $\left( Q \right)$.
Vận dụng 1 trang 122 Toán 11 tập 1
Tìm ảnh của hình hộp $ABEF.DCGH$ qua phép chiếu song song được mô tả trong Hình 3.
Lời giải:
Ảnh của hình hộp $ABEF.DCGH$ qua phép chiếu song song được mô tả trong Hình 3 là hình $A’B’E’F’.D’C’G’H’$
Hoạt động 2 trang 122 Toán 11 tập 1
Trong Hình 4, xét phép chiếu theo phương $l$ lên mặt phẳng $\left( P \right)$, mặt phẳng $\left( Q \right)$ chứa đường thẳng $a$ và song song với phương chiếu.
a) Khi điểm $M$ thay đổi trên đường thẳng $a$ thì ảnh $M’$ của nó thay đổi ở đâu?
b) Từ đó hãy chỉ ra ảnh của đường thẳng $a$ qua phép chiếu theo phương $l$ lên mặt phẳng $\left( P \right)$.
Lời giải:
a) Khi điểm $M$ thay đổi trên đường thẳng $a$ thì ảnh $M’$ của nó thay đổi trên đường thẳng $a’$.
b) Ảnh của đường thẳng $a$ qua phép chiếu theo phương $l$ lên mặt phẳng $\left( P \right)$ là đường thẳng $a’$.
Giải Toán 11 tập 1 trang 23
Hoạt động 3 trang 123 Toán 11 tập 1
Trong Hình 5, xét phép chiếu theo phương $l$ với mặt phẳng chiếu $\left( P \right)$. Biết $a\parallel b$ với $a \subset \left( Q \right)$ và $b \subset \left( R \right)$. Nêu nhận xét về vị trí tương đối của hình chiếu $a’,b’$ của $a,b$ trong hai trường hợp: $\left( Q \right)\parallel \left( R \right);\left( Q \right) \equiv \left( R \right)$.
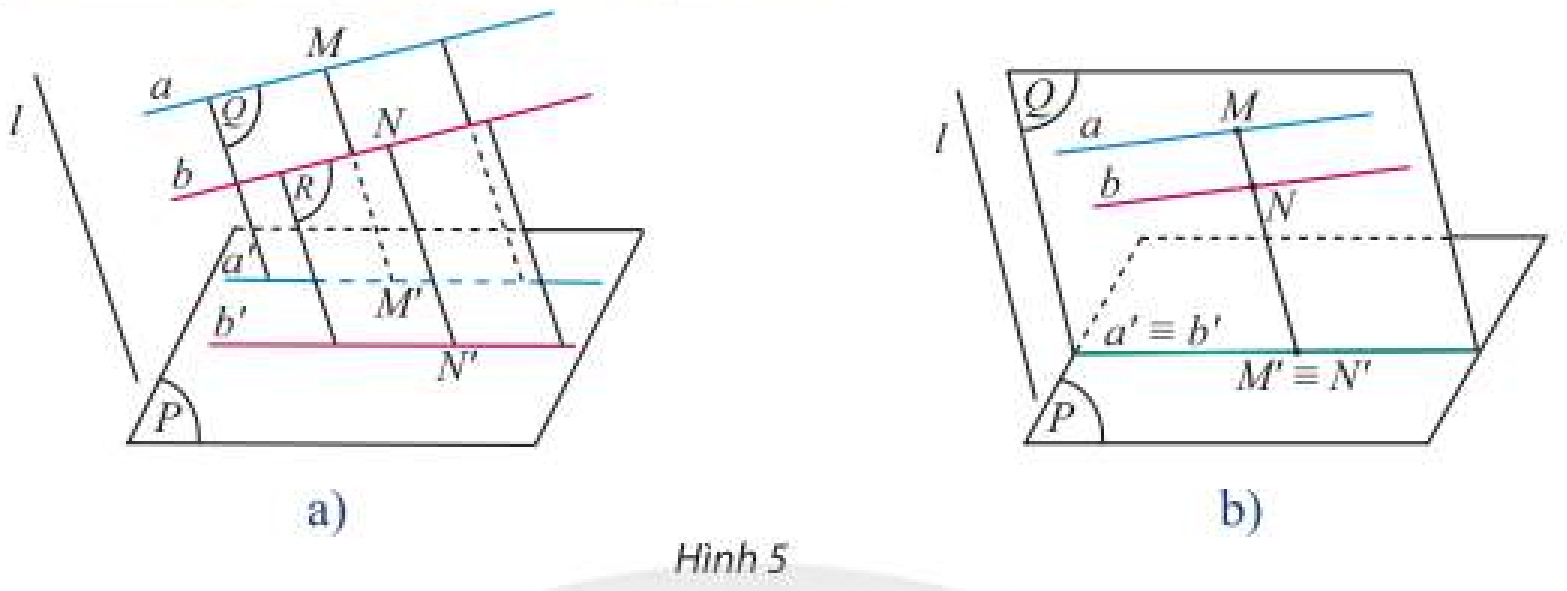
Lời giải:
Ta có:
$\left. \begin{array}{l}\left( Q \right)\parallel \left( R \right)\\\left( P \right) \cap \left( Q \right) = a’\\\left( P \right) \cap \left( R \right) = b’\end{array} \right\} \Rightarrow a’\parallel b’$
Vậy nếu $\left( Q \right)\parallel \left( R \right)$ thì $a’\parallel b’$; nếu $\left( Q \right) \equiv \left( R \right)$ thì $a’ \equiv b’$.
Giải Toán 11 tập 1 trang 124
Thực hành 2 trang 124 Toán 11 tập 1
Cho hình thang $ABCD$ có đáy lớn $AB$ và $AB = 2CD$, hình chiếu song song của $ABCD$ là tứ giác $A’B’C’D’$. Chứng minh rằng $A’B’C’D’$ cũng là một hình thang và $A’B’ = 2C’D’$.
Lời giải:
$ABCD$ là hình thang có đáy lớn $AB \Rightarrow AB\parallel CD$.
Vì hình chiếu song song của hai đường thẳng song song là hai đường thẳng song song hoặc trùng nhau, mà hình chiếu song song của $ABCD$ là tứ giác $A’B’C’D’$ nên $A’B’\parallel C’D’$. Vậy $A’B’C’D’$ cũng là một hình thang.
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau, mà $AB = 2CD,AB\parallel CD$ và $A’B’\parallel C’D’$ nên $A’B’ = 2C’D’$.
Vận dụng 2 trang 124 Toán 11 tập 1
Cho $G$ là trọng tâm tam giác $ABC$, $M$ là trung điểm $BC$ và hình chiếu song song của tam giác $ABC$ là tam giác $A’B’C’$. Chứng minh rằng hình chiếu $M’$ của $M$ là trung điểm của $B’C’$ và hình chiếu $G’$ của $G$ cũng là trọng tâm tam giác $A’B’C’$.
Lời giải:
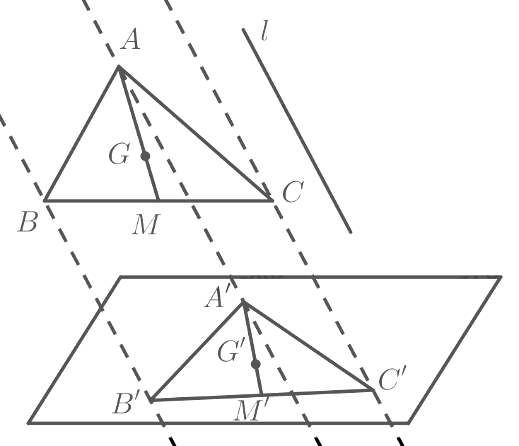
Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có $M$ nằm giữa $B$ và $C$ thì $M’$ nằm giữa $B’$ và $C’$.
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có $MB = MC$ thì $M’B’ = M’C’$.
Vậy $M’$ là trung điểm của $B’C’$.
Vì phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó nên có $G$ nằm giữa $A$ và $M$ thì $G’$ nằm giữa $A’$ và $M’$.
Vì phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc trùng nhau nên có $AG = \frac{2}{3}AM$ thì $A’G’ = \frac{2}{3}A’M’$.
Vậy $G’$ là trọng tâm tam giác $A’B’C’$.
Hoạt động 4 trang 124 Toán 11 tập 1
Quan sát Hình 7 và cho biết các tia nắng song song đã tạo ra hình chiếu của hình hộp như thế nào trên nền nhà.
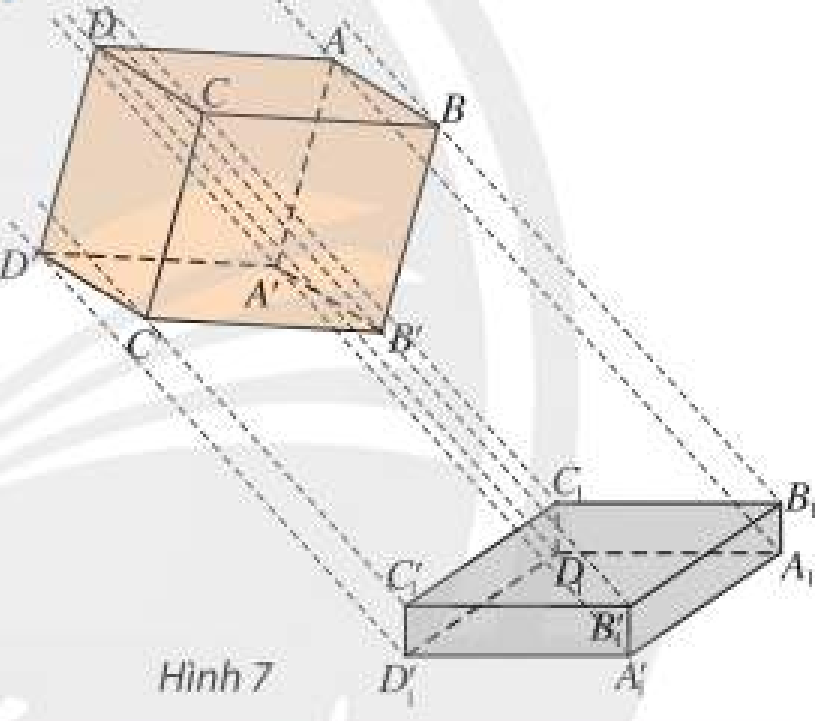
Lời giải:
Các tia nắng song song đã tạo ra hình chiếu của hình hộp trên nền nhà là hình đa giác ${A_1}{B_1}{C_1}{{\rm{D}}_1}.{A_1}{\rm{‘}}{B_1}{\rm{‘}}{C_1}{\rm{‘}}{{\rm{D}}_1}{\rm{‘}}$.
Giải Toán 11 tập 1 trang 126
Thực hành 3 trang 126 Toán 11 tập 1
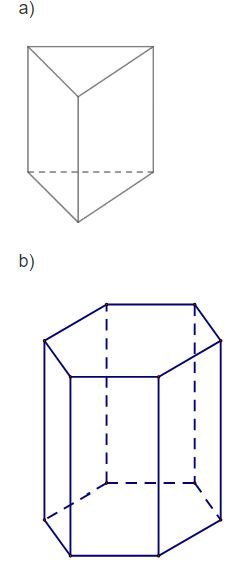
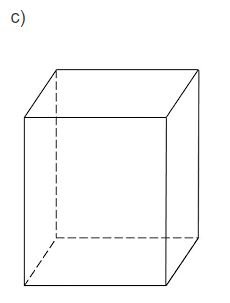
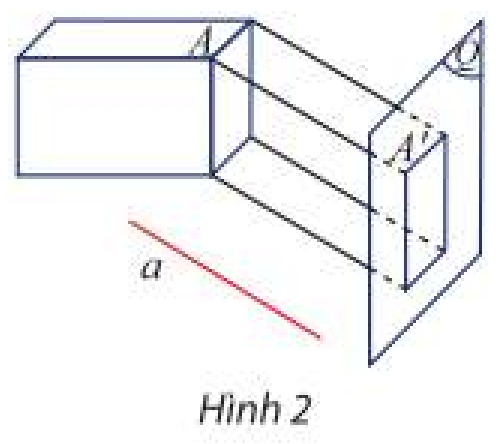
Gọi tên các hình khối có hình biểu diễn là các hình trong Hình 10.
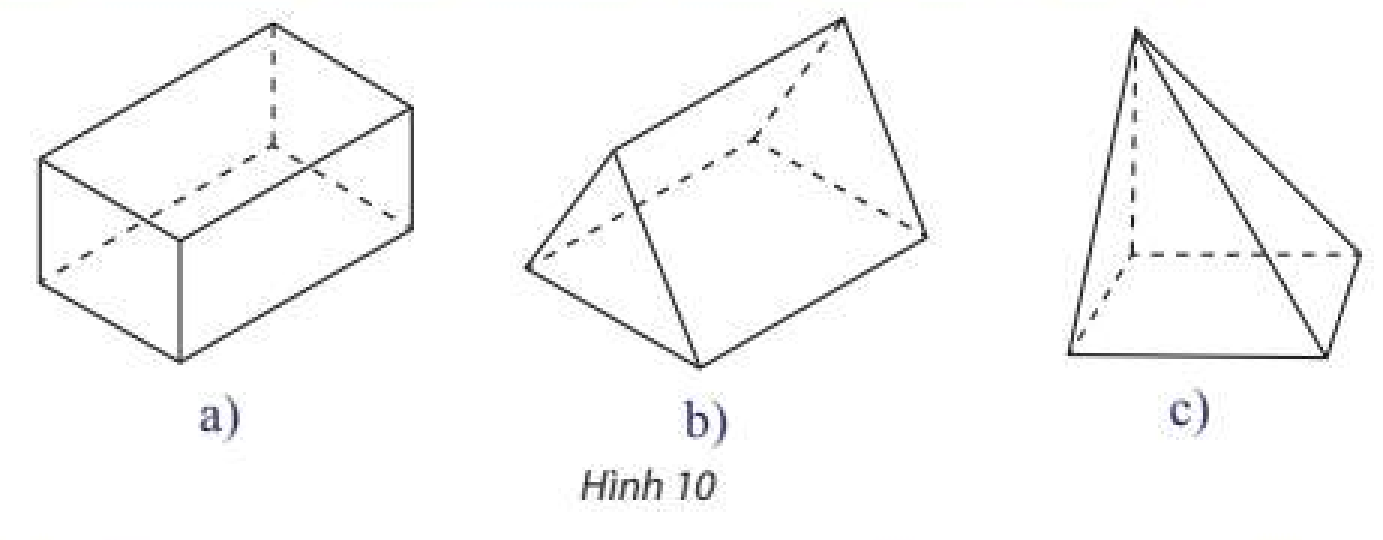
Lời giải:
Hình a: Hình hộp.
Hình b: Hình lăng trụ tam giác.
Hình c: Hình chóp tứ giác.
Thực hành 3 trang 126 Toán 11 tập 1
Vẽ hình biểu diễn của một hình chóp tam giác $S.ABC$ đặt trên một hình lăng trụ tam giác $ABC.A’B’C’$.
Lời giải:
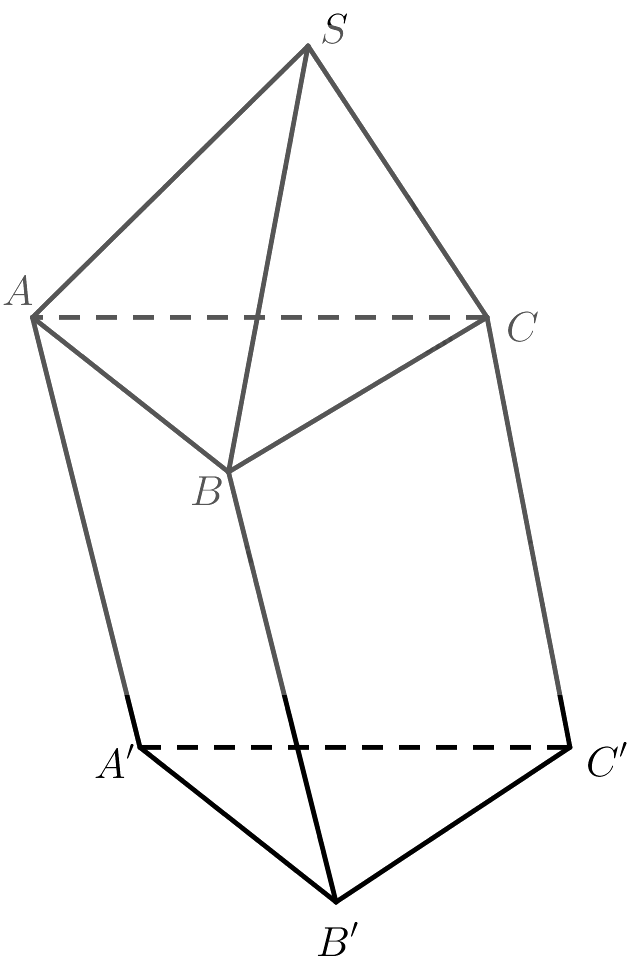
Giải bài 1 trang 126 Toán 11 tập 1
Trong các mệnh đề sau, mệnh đề nào đúng?
a) Một đường thẳng có thể song song với hình chiếu của nó;
b) Một đường thẳng có thể trùng với hình chiếu của nó;
c) Hình chiếu song song của hai đường thẳng chéo nhau có thể song song với nhau;
d) Hình chiếu song song của hai đường thẳng chéo nhau có thể trùng nhau.
Lời giải
Mệnh đề a đúng trong trường hợp đường thẳng song song với mặt phẳng chiếu.
Mệnh đề b đúng trong trường hợp đường thẳng nằm trên mặt phẳng chiếu.
Giả sử $a$ và $b$ là hai đường thẳng chéo nhau có hình chiếu là $a’$ và $b’$. Nếu $mp\left( {a,a’} \right)\parallel mp\left( {b,b’} \right)$ thì $a’\parallel b’$. Vậy mệnh đề c đúng.
Nếu hình chiếu song song của hai đường thẳng mà trùng nhau thì hai đường thẳng đó cùng thuộc một mặt phẳng. Vậy mệnh đề d sai.
Giải bài 2 trang 126 Toán 11 tập 1
Vẽ hình biểu diễn của một lục giác đều.
Lời giải
Lục giác đều có các cặp cạnh đối bằng nhau và song song với nhau, các đường chéo của 2 đỉnh đối diện cắt nhau tại trung điểm mỗi đường. Vậy ta có hình biểu diễn như sau:
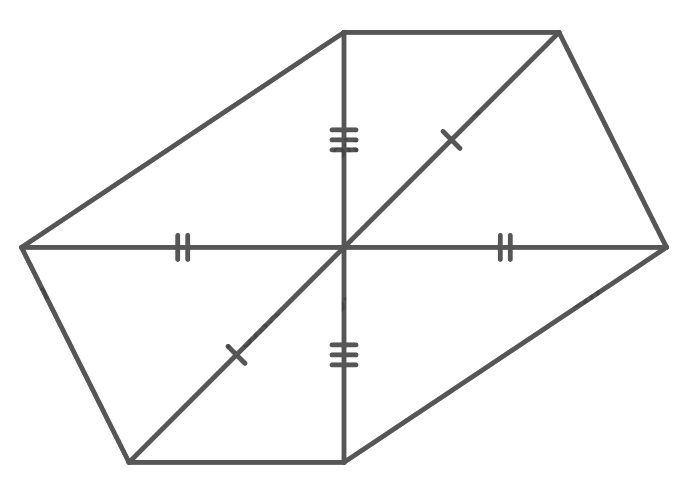
Giải bài 3 trang 126 Toán 11 tập 1
Vẽ hình biểu diễn của một hình vuông nội tiếp trong một hình tròn
Bài làm
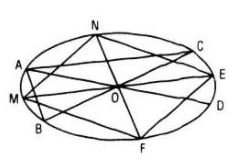
Giải bài 4 trang 126 Toán 11 tập 1
Cho hai điểm A, B nằm ngoài mặt phẳng (α) và đường thẳng d cắt (α). Giả sử đường thẳng AB cắt (α) tại điểm O. Gọi A’ và B’ lần lượt là hình chiếu song song của A và B trên (α) theo phương của đường thẳng d. Ba điểm O, A’, B’ thẳng hàng không? Vì sao? Chọn d sao cho:
a) A’B’ = AB
b) A’B’ = 2AB
Bài làm
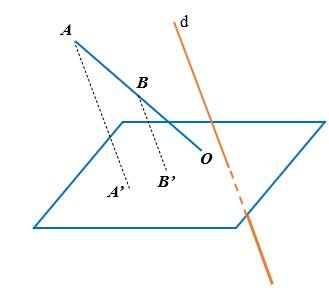
Giải bài 5 trang 126 Toán 11 tập 1
Vẽ hình biểu diễn của:
a) Hình lăng trụ có đáy là tam giác đều
b) Hình lăng trụ có đáy là lục giác đều
c) Hình hộp
Bài làm