Giải Toán 11 tập 1 trang 135 bài 1: Số trung bình và mốt của mẫu số liệu ghép nhóm
Giải Toán 11 tập 1 trang 135 bài 1: Số trung bình và mốt của mẫu số liệu ghép nhóm
Giải toán 11 tập 1 trang 135 Bài 1 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 11 Chân trời sáng tạo. Mời các em học sinh cùng quý phụ huynh tham khảo.
Giải Toán 11 tập 1 trang 130
Hoạt động 1 trang 130 Toán 11 tập 1
Sử dụng dữ liệu ở biểu đồ trong Hoạt động mở đầu hoàn thiện bảng thống kê về số số lượng khách hàng nữ theo tuổi sau:

Lời giải:
| Khoảng tuổi | [20; 30) | [30; 40) | [40; 50) | [50; 60) | [60; 70) |
| Số khách hàng nữ | 3 | 9 | 6 | 3 | 2 |
Giải Toán 11 tập 1 trang 132
Thực hành 1 trang 132 Toán 11 tập 1
Một cửa hàng đã thống kê số ba lỗ bán được mỗi ngày trong tháng 9 với kết quả cho như sau:
![]()
Hãy chia mẫu số liệu trên thành 5 nhóm, lập tần số ghép nhóm, hiệu chỉnh bảng và xác định giá trị đại diện cho mỗi nhóm.
Lời giải:
Khoảng biến thiên của mẫu số liệu trên là $R = 29 – 10 = 19$.
Độ dài mỗi nhóm $L > \frac{R}{k} = \frac{{19}}{5} = 3,8$.
Ta chọn $L = 4$ và chia dữ liệu thành các nhóm: $\left[ {10;14} \right),\left[ {14;18} \right),\left[ {18;22} \right),\left[ {22;26} \right),\left[ {26;30} \right)$.
Khi đó ta có bảng tần số ghép nhóm sau:
| Số ba lô đã bán | [10; 14) | [14; 18) | [18; 22) | [22; 26) | [26; 30) |
| Giá trị đại diện | 12 | 16 | 20 | 24 | 28 |
| Số ngày | 8 | 5 | 8 | 3 | 6 |
Hoạt động 2 trang 132 Toán 11 tập 1
Các bạn học sinh lớp 11A1 trả lời 40 câu hỏi trong một bài kiểm tra. Kết quả được thống kê ở bảng sau:

a) Tính giá trị đại diện ${c_i},1 \le i \le 5$, của từng nhóm số liệu.
b) Tính ${n_1}{c_1} + {n_2}{c_2} + {n_3}{c_3} + {n_4}{c_4} + {n_5}{c_5}$.
c) Tính $\bar x = \frac{{{n_1}{c_1} + {n_2}{c_2} + {n_3}{c_3} + {n_4}{c_4} + {n_5}{c_5}}}{{40}}$.
Lời giải:
a)
$\begin{array}{l}{c_1} = \frac{{16 + 21}}{2} = 18,5;{c_2} = \frac{{21 + 26}}{2} = 23,5;{c_3} = \frac{{26 + 31}}{2} = 28,5;\\{c_4} = \frac{{31 + 36}}{2} = 33,5;{c_3} = \frac{{36 + 41}}{2} = 38,5\end{array}$
b) ${n_1}{c_1} + {n_2}{c_2} + {n_3}{c_3} + {n_4}{c_4} + {n_5}{c_5} = 4.18,5 + 6.23,5 + 8.28,5 + 18.33,5 + 4.38,5 = 1200$.
c) $\bar x = \frac{{{n_1}{c_1} + {n_2}{c_2} + {n_3}{c_3} + {n_4}{c_4} + {n_5}{c_5}}}{{40}} = \frac{{1200}}{{40}} = 30$.
Giải Toán 11 tập 1 trang 133
Thực hành 2 trang 133 Toán 11 tập 1
Hãy ước lượng trung bình số câu trả lời đúng của các học sinh lớp 11A1 trong Hoạt động 2.
Lời giải:
$\bar x = \frac{{{n_1}{c_1} + {n_2}{c_2} + {n_3}{c_3} + {n_4}{c_4} + {n_5}{c_5}}}{{40}} = \frac{{1200}}{{40}} = 30$
Vậy số câu trả lời đúng của các học sinh lớp 11A1 là 30 câu.
Thực hành 3 trang 133 Toán 11 tập 1
Hãy ước lượng cân nặng trung bình của học sinh trong Ví dụ 2 sau khi ghép nhóm và so sánh kết quả tìm được với cân nặng trung bình của mẫu số liệu gốc.
Lời giải:
Cân nặng trung bình của học sinh sau khi ghép nhóm là:
$\bar x = \frac{{4.47 + 5.51 + 7.55 + 7.59 + 5.63}}{{28}} = 55,6\left( {kg} \right)$
Cân nặng trung bình của học sinh của mẫu số liệu gốc là:
$\bar x = 56\left( {kg} \right)$
Vậy giá trị ước lượng cân nặng trung bình của học sinh sau khi ghép nhóm xấp xỉ bằng cân nặng trung bình của học sinh của mẫu số liệu gốc.
Hoạt động 3 trang 133 Toán 11 tập 1
Từ mẫu số liệu ở Hoạt động mở đầu, hãy cho biết khách hàng nam và khách hàng nữ ở khoảng tuổi nào mua bảo hiểm nhân thọ nhiều nhất. Ta có thể biết mốt của mẫu số liệu đó không?
Lời giải:
Khách hàng nam ở khoảng tuổi $\left[ {40;50} \right)$ mua bảo hiểm nhân thọ nhiều nhất.
Khách hàng nữ ở khoảng tuổi $\left[ {30;40} \right)$ mua bảo hiểm nhân thọ nhiều nhất.
Ta có thể biết mốt của mẫu số liệu đó.
Giải Toán 11 tập 1 trang 134
Thực hành 4 trang 134 Toán 11 tập 1
Hãy sử dụng dữ liệu ở Hoạt động mở đầu để tư vấn cho đại lí bảo hiểm xác định khách hàng nam và nữ ở tuổi nào hay mua bảo hiểm nhất.
Lời giải:
• Đối với khách hàng nam:
Nhóm chứa mốt của mẫu số liệu trên là nhóm $\left[ {40;50} \right)$.
Do đó: ${u_m} = 40;{n_{m – 1}} = 6;{n_m} = 10;{n_{m + 1}} = 7;{u_{m + 1}} – {u_m} = 50 – 40 = 10$
Mốt của mẫu số liệu ghép nhóm là:
${M_O} = {u_m} + \frac{{{n_m} – {n_{m – 1}}}}{{\left( {{n_m} – {n_{m – 1}}} \right) + \left( {{n_m} – {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} – {u_m}} \right) = 40 + \frac{{10 – 6}}{{\left( {10 – 6} \right) + \left( {10 – 7} \right)}}.10 = 45,7$
Vậy ta có thể dự đoán khách hàng nam 46 tuổi có nhu cầu mua bảo hiểm nhiều nhất.
• Đối với khách hàng nữ:
Nhóm chứa mốt của mẫu số liệu trên là nhóm $\left[ {30;40} \right)$.
Do đó: ${u_m} = 30;{n_{m – 1}} = 3;{n_m} = 9;{n_{m + 1}} = 6;{u_{m + 1}} – {u_m} = 40 – 30 = 10$
Mốt của mẫu số liệu ghép nhóm là:
${M_O} = {u_m} + \frac{{{n_m} – {n_{m – 1}}}}{{\left( {{n_m} – {n_{m – 1}}} \right) + \left( {{n_m} – {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} – {u_m}} \right) = 30 + \frac{{9 – 3}}{{\left( {9 – 3} \right) + \left( {9 – 6} \right)}}.10 = 36,7$
Vậy ta có thể dự đoán khách hàng nữ 37 tuổi có nhu cầu mua bảo hiểm nhiều nhất.
Giải bài 1 trang 134 Toán 11 tập 1
Anh Văn ghi lại cự li 30 lần ném lao của minh ở bảng sau (đơn vị: mét)
| 72,1 | 72,9 | 70,2 | 70,9 | 72,2 | 71,5 | 72,5 | 69,3 | 72,3 | 69,7 |
| 72,3 | 71,5 | 71,2 | 69,8 | 72,3 | 71,1 | 69,5 | 72,2 | 71,9 | 73,1 |
| 71,6 | 71,3 | 72,2 | 71,8 | 70,8 | 72,2 | 72,2 | 72,9 | 72,7 | 70,7 |
a) Tính cự li trung bình của mỗi lần ném
b) Tổng hợp lại kết quả ném của anh Văn vào bảng tần số ghép nhóm theo mẫu sau:
| Cự li (m) | [69,2;70) | [70;70,8) | [70,8;71,6) | [71,6;72,4) | [72,4;73,2) |
| Số lần | ? | ? | ? | ? | ? |
c) Hãy ước lượng cự li trung bình mỗi lần ném từ bảng tần số ghép nhóm trên
d) Khả năng anh Văn ném được khoảng bao nhiêu mét là cao nhất
Bài làm
a) Cự li trung bình của mỗi lần ném là 71,6 (m)
b)
| Cự li (m) | [69,2;70) | [70;70,8) | [70,8;71,6) | [71,6;72,4) | [72,4;73,2) |
| Số lần | 4 | 2 | 9 | 10 | 5 |
c)
| Cự li (m) | [69,2;70) | [70;70,8) | [70,8;71,6) | [71,6;72,4) | [72,4;73,2) |
| Giá trị đại diện | 69,6 | 70,4 | 71,2 | 72 | 72,8 |
| Số lần | 4 | 2 | 9 | 10 | 5 |
Cự li trung bình mỗi lần ném xấp xỉ bằng $\frac{69,6.4+70,4.2+71,2.9+72.10+72,8.5}{30}= 71,5$ (m)
d) Nhóm chứa mốt của mẫu số liệu trên là [71,6; 72,4)
Do đó: $u_{m}=71,6; n_{m-1} = 9; n_{m+1}=5; u_{m+1}-u_{m} = 72,4-71,6=0,8$
Mốt của mẫu số liệu ghép nhóm là:
$M_{0} = 71,6 + \frac{10-9}{(10-9)+(10-5)}.0,8 = 71,7$ (m)
Vậy khả năng anh Văn ném được 71,7 m là cao nhất
Giải bài 2 trang 135 Toán 11 tập 1
Người ta đếm số xe ô tô đi qua một trạm thu phí mỗi phút trong khoảng thời gian từ 9 giờ đến 9 giờ 30 phút sáng. Kết quả được ghi lại ở bảng sau:
| 15 | 16 | 13 | 21 | 17 | 23 | 15 | 21 | 6 | 11 | 12 | 23 | 19 | 25 | 11 |
| 25 | 7 | 29 | 10 | 28 | 29 | 24 | 6 | 11 | 23 | 11 | 21 | 9 | 27 | 15 |
a) Tìm số xe trung bình đi qua trạm thu phí trong mỗi phút
b) Tổng hợp lại số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:
| Số xe | [6;10] | [11;15] | [16;20] | [21;25] | [26;30] |
| Số lần | ? | ? | ? | ? | ? |
c) Hãy ước lượng trung bình số xe đi qua trạm thu phí trong mỗi phút từ bảng tần số ghép nhóm trên.
Bài làm
a) Số xe trung bình đi qua trạm thu phí trong mỗi phút là 17,4 xe
b)
| Số xe | [6;10] | [11;15] | [16;20] | [21;25] | [26;30] |
| Số lần | 5 | 9 | 3 | 9 | 4 |
c) Hiệu chỉnh lại bảng số liệu ta có:
| Số xe | [5,5; 10,5) | [10,5;15,5) | [15,5;20,5) | [20,5;25,5) | [25,5;30,5) |
| Giá trị đại diện | 8 | 13 | 18 | 23 | 28 |
| Số lần | 5 | 9 | 3 | 9 | 4 |
Trung bình số xe đi qua trạm thu phí mỗi phút xấp xỉ bằng:
$\frac{8.5+13.9+18.3+23.9+28.4}{30} = 17,7$
Giải bài 3 trang 135 Toán 11 tập 1
Một thư viện thống kế số lượng sách được mượn mỗi ngày trong ba tháng ở bảng sau:
| Số sách | [16;20] | [21;25] | [26;30] | [31;35] | [36;40] | [41;45] | [46;50] |
| Số ngày | 3 | 6 | 15 | 27 | 22 | 14 | 5 |
Hãy ước lượng số trung bình và mốt của mẫu số liệu ghép nhóm trên.
Bài làm
Số liệu trên được hiệu chỉnh như sau:
| Số sách | [15,5;20,5) | [20,5;25,5) | [25,5;30,5) | [30,5;35,5) | [35,5;40,5) | [40,5;45,5) | [45,5;50,5) |
| Giá trị đại diện | 18 | 23 | 28 | 33 | 38 | 43 | 48 |
| Số ngày | 3 | 6 | 15 | 27 | 22 | 14 | 5 |
Số sách được mượn trung bình mỗi ngày xấp xỉ bằng:
(18.3 + 23.6 + 28.15 + 33.27 + 38.33 + 43.14 + 48.5) : 92 = 34,6
Nhóm chứa mốt của mẫu số liệu là [30,5;35,5)
Do đó $u_{m}=30,5; n_{m-1} = 15, n_{m+1}=22, u_{m+1} – u_{m} = 35,5 – 30,5 = 5$
Mốt của mẫu số liệu ghép nhóm là:
$M_{0} = 30,5 + \frac{27-15}{(27-15)+(27-22)}.5 = 34$
Giải bài 4 trang 135 Toán 11 tập 1
Kết quả đo chiều cao của 200 cây keo 3 năm tuổi ở một nông trường được biểu diễn ở biểu đồ dưới đây
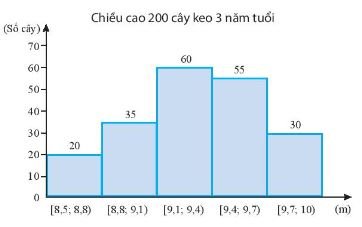
Hãy ước lượng số trung bình và mốt của mẫu số liệu ghép nhóm trên.
Lời giải
Chiều cao của 200 cây keo 3 năm tuổi được thống kê trong bảng sau:
| Chiều cao của cây | [8,5; 8,8) | [8,8; 9,1) | [9,1; 9,4) | [9,4; 9,7) | [9,7; 10) |
| Giá trị đại diện | 8,65 | 8,95 | 9,25 | 9,55 | 9,85 |
| Số cây | 20 | 35 | 60 | 55 | 30 |
Chiều cao của 200 cây keo 3 năm tuổi sau khi ghép nhóm là:
$\bar x = \frac{{20.8,65 + 35.8,95 + 60.9,25 + 55.9,55 + 30.9,85}}{{200}} = 9,31\left( m \right)$
Nhóm chứa mốt của mẫu số liệu trên là nhóm $\begin{array}{*{20}{c}}{\left[ {9,1;9,4} \right)}\end{array}$.
Do đó: ${u_m} = 9,1;{n_{m – 1}} = 35;{n_m} = 60;{n_{m + 1}} = 55;{u_{m + 1}} – {u_m} = 9,4 – 9,1 = 0,3$
Mốt của mẫu số liệu ghép nhóm là:
${M_O} = {u_m} + \frac{{{n_m} – {n_{m – 1}}}}{{\left( {{n_m} – {n_{m – 1}}} \right) + \left( {{n_m} – {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} – {u_m}} \right) = 9,1 + \frac{{60 – 35}}{{\left( {60 – 35} \right) + \left( {60 – 55} \right)}}.0,3 = 9,35$
Vậy chiều cao của 200 cây keo 3 năm tuổi nhiều nhất là 9,35 mét.
