Giải Toán 11 tập 1 trang 19 Bài 2: Giá trị lượng giác của một góc lượng giác

Giải toán 11 tập 1 trang 19 Bài 2 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 11 Chân trời sáng tạo. Mời các em học sinh cùng quý phụ huynh tham khảo.

Giải Toán 11 tập 1 trang 13

Hoạt động 1 trang 13 Toán 11 tập 1

Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác $\frac{{2\pi }}{3}$ và $\frac{\pi }{4}$ trên

đường tròn lượng giác. Xác định tọa độ của M và N trong hệ trục tọa độ Oxy .

Lời giải:

Gọi B, C lần lượt là hình chiếu của M lên Ox, Oy

D,E lần lượt là hình chiếu của N lên Ox, Oy

Ta có OM = ON = 1

$\widehat {MOC} = \frac{{2\pi }}{3} – \frac{\pi }{2} = \frac{\pi }{6} \Rightarrow \left\{ \begin{array}{l}\sin \widehat {MOC} = \frac{1}{2} = \frac{{MC}}{{OM}} \Rightarrow MC = \frac{1}{2}\\\cos \widehat {MOC} = \frac{{\sqrt 3 }}{2} = \frac{{MB}}{{OM}} \Rightarrow MB = \frac{{\sqrt 3 }}{2}\end{array} \right.$

Do điểm M có hoành độ nằm bên trái trục Ox nên tọa độ của điểm M $\left( {\frac{-1}{2};\frac{{\sqrt 3 }}{2}} \right)$

$\widehat {NOD} = – \frac{\pi }{4} \Rightarrow \left\{ \begin{array}{l}\sin \widehat {NOD} = – \frac{{\sqrt 2 }}{2} = \frac{{ND}}{{ON}} \Rightarrow ND = – \frac{{\sqrt 2 }}{2}\\\cos \widehat {NOD} = \frac{{\sqrt 2 }}{2} = \frac{{NE}}{{ON}} \Rightarrow NE = \frac{{\sqrt 2 }}{2}\end{array} \right.$

Tọa độ của điểm N $\left( {  \frac{{\sqrt 2 }}{2};\frac{-{\sqrt 2 }}{2}} \right)$

Giải Toán 11 tập 1 trang 15

Thực hành trang 15 Toán 11 tập 1

Tính $\sin \left( { – \frac{{2\pi }}{3}} \right)$ và $\tan 495^\circ $

Lời giải:

$\begin{l}\sin \left( { – \frac{{2\pi }}{3}} \right) = – \frac{{\sqrt 3 }}{2}\\\tan 495^\circ = – 1\end{mảng}$

Giải Toán 11 tập 1 trang 16

Thực hành 2 trang 16 Toán 11 tập 1

Sử dụng máy tính cầm tay để tính

$\cos 75^\circ \,\,$và $\tan \left( { – \frac{{19\pi }}{6}} \right)$

Lời giải:

$\begin{l}\cos 75^\circ = \frac{{\sqrt 6 – \sqrt 2 }}{4}\\\tan \left( { – \frac{{19\pi }}{6}} \right) = – \frac{{\sqrt 3 }}{3}\end{mảng}$

Hoạt động 2 trang 16 Toán 11 tập 1

a)    Trong Hình 5, M là điểm biểu diễn của góc lượng giác α trên đường tròn lượng giác. Giải thích vì sao ${\sin ^2}\alpha  + {\cos ^2}\alpha  = 1$

b)    Chia cả hai vế của biểu thức ở câu a) cho ${\cos ^2}\alpha $ ta được đẳng thức nào?

c)    Chia cả hai vế của biểu thức ở câu a) cho ${\sin ^2}\alpha $ ta được đẳng thức nào?

Lời giải:

a) Thực hiện $\begin{array}{l}\sin \alpha = MH \Rightarrow {\sin ^2}\alpha = M{H^2}\\\cos \alpha = OH \Rightarrow {\cos ^2}\alpha = O{H^2}\end{array}$

Áp dụng định lý Py – Ta – Go vào tam giác OMH vuông tại H ta có:

$\begin{array}{l}M{H^2} + O{H^2} = O{M^2} = 1\\ \Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1\end{array}$

b)    Chia cả hai vế cho ${\cos ^2}\alpha $, ta được:

$\begin{array}{l}\frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\\ \Leftrightarrow {\tan ^2}\alpha + 1 = \frac{1}{{{{\cos }^2}\alpha }}\end{array}$

c)    Chia cả hai vế cho ${\sin ^2}\alpha $, ta được:

$\begin{array}{l}\frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\\ \Leftrightarrow {\cot ^2}\alpha + 1 = \frac{1}{{{{\sin }^2}\alpha }}\end{array}$

Giải Toán 11 tập 1 trang 17

Thực hành 3 trang 17 Toán 11 tập 1

Cho $\tan \alpha  = \frac{2}{3}$ với $\pi  < \alpha  < \frac{{3\pi }}{2}$. Tính $\cos \alpha $ và $\sin \alpha $

Lời giải:

Ta có:

 $\begin{array}{l}{\tan ^2}\alpha + 1 = \frac{1}{{{{\cos }^2}\alpha }}\\ \Rightarrow {\left( {\frac{2}{3}} \right)^2} + 1 = \frac{1}{{{{\cos }^2}\alpha }}\\ \Rightarrow \frac{1}{{{{\cos }^2}\alpha }} = \frac{{13}}{9}\\ \Rightarrow \cos \alpha = \pm \frac{{3\sqrt {13} }}{{13}}\end{array}$

Thực hiện $\pi < \alpha < \frac{{3\pi }}{2} \Rightarrow \cos \alpha = – \frac{{3\sqrt {13} }}{{13}}$

Trong đó: $\begin{array}{l}\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} \Rightarrow \frac{2}{3} = \sin \alpha : \left( { – \frac{{3\sqrt {13} }}{{13}}} \right)\\ \Rightarrow \sin \alpha = – \frac{{2\sqrt {13} }}{{13}}\end{array}$

Hoạt động 3 trang 17 Toán 11 tập 1

Cho $\alpha  = \frac{\pi }{3}$. Biểu diễn các góc lượng giác $ – \alpha ,\alpha  + \pi ,\pi  – \alpha ,\frac{\pi }{2} – \alpha $ trên đường tròn lượng giác và rút ra mỗi liên hệ giữ giá trị lượng giác của các góc này với giá trị lượng giác của góc $\alpha $

Lời giải:

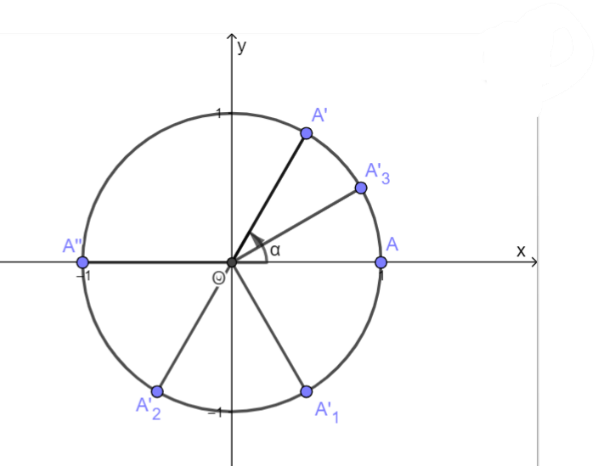
Dựa vào đường tròn lượng giác ta nhận được:

$\left. \begin{mảng}{l}\sin \left( { – \alpha } \right) = – \sin \alpha \\\cos \left( { – \alpha } \right) = \cos \alpha \end{mảng} \right\} \Rightarrow \left\{ \begin{mảng}{l}tan\left( { – \alpha } \right) = – \tan \alpha \\\cot \left( { – \alpha } \right) = – \cot \alpha \end{mảng} \right.$

$\left. \begin{mảng}{l}\sin \left( {\pi + \alpha } \right) = – \sin \alpha \\\cos \left( {\pi + \alpha } \right) = – \cos \alpha \end{mảng} \right\} \Rightarrow \left\{ \begin{mảng}{l}\tan \left( {\pi + \alpha } \right) = \tan \alpha \\\cot \left( {\pi + \alpha } \right) = \cot \alpha \end{mảng} \right.$

$\begin{mảng}{l}\trái. \begin{mảng}{l}\sin \left( {\pi – \frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2},\,\,\,\sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\\\cos \left( {\pi – \frac{\pi }{3}} \right) = – \frac{1}{2},\,\,\cos \frac{\pi }{3} = \frac{1}{2}\end{mảng} \right\} \Rightarrow \left\{ \begin{mảng}{l}\sin \left( {\pi – \frac{\pi }{3}} \right) = \sin \frac{\pi }{3}\\\cos \left( {\pi – \frac{\pi }{3}} \right) = – \cos \frac{\pi }{3}\end{mảng} \right. \Rightarrow \left\{ \begin{mảng}{l}\sin \left( {\pi – \alpha } \right) = \sin \alpha \\\cos \left( {\pi – \alpha } \right) = – \cos \alpha \end{mảng} \right.\\ \Rightarrow \left\{ \begin{mảng}{l}\tan \left( {\pi – \alpha } \right) = – \tan \alpha \\\cot \left( {\pi – \alpha } \right) = – \cot \alpha \end{mảng} \right.\end{mảng}$

$\begin{mảng}{l}\trái. \begin{array}{l}\sin \left( {\frac{\pi }{2} – \frac{\pi }{3}} \right) = \frac{1}{2},\,\,\sin \frac{\pi }{3} = \frac{{\sqrt 3 }}{2}\\\cos \left( {\frac{\pi }{2} – \frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2},\,\,\cos \frac{\pi }{3} = \frac{1}{2}\end{array} \right\} \Rightarrow \left\{ \begin{array}{l}\sin \left( {\frac{\pi }{2} – \frac{\pi }{3}} \right) = \cos \frac{\pi }{3}\\\cos \left( {\frac{\pi }{2} – \frac{\pi }{3}} \phải) = \sin \frac{\pi }{3}\end{mảng} \phải. \phảimũi tên \trái\{ \begin{mảng}{l}\sin \left( {\frac{\pi }{2} – \alpha } \phải) = \cos \alpha \\\cos \left( {\frac{\pi }{2} – \alpha } \phải) = \sin \alpha \end{mảng} \phải.\\ \phảimũi tên \trái\{ \begin{mảng}{l}\tan \left( {\frac{\pi }{2} – \alpha } \phải) = \cot \alpha \\\cot \left( {\frac{\pi }{2} – \alpha } \phải) = \tan \alpha \end{mảng} \phải.\end{mảng}$

Giải Toán 11 tập 1 trang 19

Thực hành 4 trang 19 Toán 11 tập 1

a)    Biểu diễn $\cos 638^\circ $ qua gí trị lượng giác của góc có số đo từ $0^\circ $ đến $45^\circ $

b)    Biểu diễn $\cot \frac{{19\pi }}{5}$ qua giá trị lượng giác của góc có số đo từ 0 đến $\frac{\pi }{4}$

Lời giải:

a) $\cos 638^\circ = \cos \left( {4.180^\circ + 90^\circ – 8^\circ } \right) = – \cos \left( {90^\circ – 8^\circ } \right) = – \sin 8^\circ $

b) $\cot \left( {\frac{{19\pi }}{5}} \right) = \cot \left( {4\pi – \frac{\pi }{5}} \right) = – \cot \left( {\frac{\pi }{5}} \right)$

Vận dụng trang 19 Toán 11 tập 1

Trong Hình 11, vị trí cabin mà Bình và Cường ngồi trên vòng quay được đánh dấu với điểm B và C.

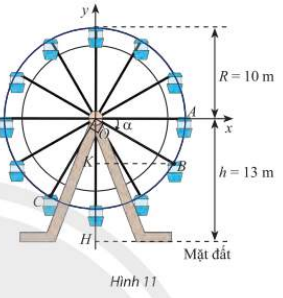
a) Chứng minh rằng chiều cao từ điểm B đến mặt đất bằng $\left( {13 + 10\sin \alpha } \right)$ mét với α là số đo của một góc lượng giác tia đầu OA, tia cuối OB. Tính độ cao của điểm B so với mặt đất khi $\alpha  =  – 30^\circ $

b) Khi điểm B cách mặt đất 4m thì điểm C cách mặt đất bao nhiêu mét? Làm tròn kết quả đến hàng phần trăm.

Lời giải:

a) Chiều cao từ điểm B đến mặt đất là độ dài đoạn KH.

Điểm B là điểm biểu diễn cho góc lượng giác có số đo góc là $\alpha $ trên đường tròn lượng giác có bán kính bằng 10 nên tọa độ điểm $B(10\cos \alpha ;10\sin \alpha )$.

Vì tung độ điểm B có giá trị âm nên $10\sin \alpha  < 0$, suy ra độ dài $OH = \left| {10\sin \alpha } \right| =  – 10\sin \alpha $.

Ta có $KH = OH – OK = 13 – ( – 10\sin \alpha ) = 13 + 10\sin \alpha $ (đã gặp).

Với $\alpha = – 30^\circ \Rightarrow KH = 13 + 10.\sin \left( { – 30^\circ } \right) = 8\,\,\left( m \right)$.

b) Nếu B cách mặt đất 4m $ \Rightarrow 4 = 13 + 10\sin \alpha  \Leftrightarrow \sin \alpha  =  – \frac{9}{{10}}$.

Ta có: ${\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Leftrightarrow {\left( { – \frac{9}{{10}}} \right)^2} + {\cos ^2}\alpha = 1 \Leftrightarrow \cos \alpha = – \frac{{\sqrt {19} }}{{10}}$.

Gọi M là hình chiếu của C lên OH.

$ \Rightarrow \cos \left( {\widehat {COH}} \right) = \sin \left( {\frac{\pi }{2} – \alpha } \right) = \cos \alpha = – \frac{{\sqrt {19} }}{{10}}$.

Mà $\cos \widehat {COH} = \frac{{OM}}{{OC}} \Rightarrow – \frac{{\sqrt {19} }}{{10}} = \frac{{OM}}{{OC}} \Rightarrow OM \approx 4,36\,\,\left( m \right)$.

$\Rightarrow MH = OH – OM = h – OM = 13 – 4,36 = 8,64 m $.

Vậy điểm C cách mặt đất  8,64 m.

Giải bài 1 trang 19 Toán 11 tập 1

Các đẳng thức sau có thể đồng thời xảy ra không?

a)    $\sin \alpha  = \frac{3}{5}$ và $\cos \alpha  =  – \frac{4}{5}$

b)    $\sin \alpha  = \frac{1}{3}$ và $\cot \alpha  = \frac{1}{2}$

c)    $\tan \alpha  = 3$ và $\cot \alpha  = \frac{1}{3}$

Lời giải

a) Ta có: ${\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Leftrightarrow {\left( {\frac{3}{5}} \right)^2} + {\cos ^2}\alpha = 1 \Leftrightarrow \cos \alpha = \pm \frac{4}{5}$

Đẳng thức có thể đồng thời xảy ra

b) Ta có: $1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }} \Rightarrow 1 + {\cot ^2}\alpha = \frac{1}{{{{\left( {\frac{1}{3}} \right)}^2}}} \Rightarrow \cot \alpha = \pm 2\sqrt 2 $

Hai đẳng thức không thể đồng thời xảy ra

c) Ta c: $\tan \alpha .\cot \alpha = 1 \Rightarrow 3.\cot \alpha = 1 \Rightarrow \cot \alpha = \frac{1}{3}$

Đẳng thức có thể đồng thời xảy ra.

Giải bài 2 trang 19 Toán 11 tập 1

Cho $\sin \alpha  = \frac{{12}}{{13}}$ và $\cos \alpha  =  – \frac{5}{{13}}$. Tính $\sin \left( { – \frac{{15\pi }}{2} – \alpha } \right) – \cos \left( {13\pi  + \alpha } \right)$

Lời giải

Ta có:

 $\begin{array}{l}\sin \left( { – \frac{{15\pi }}{2} – \alpha } \right) – \cos \left( {13\pi + \alpha } \right) = \sin \left( { -\frac{{16\pi }}{2} +\frac{{\pi }}{2} + \alpha } \right) – \cos \left( {12\pi + \pi + \alpha } \right) = \sin \left( {-8\pi + \frac{\pi }{2} – \alpha } \right) – \cos \left( { \pi + \alpha } \right) \\ = \sin \left( {\frac{\pi }{2} – \alpha } \right) + \cos \left( \alpha \right) = \cos \left( \alpha \right) + \cos \left( \alpha \right) = 2\cos \left( \alpha \right) = 2.\left( { – \frac{5}{{13}}} \right) = \frac{{ – 10}}{{13}}\end{mảng}$

Giải bài 3 trang 19 Toán 11 tập 1

Tính các giá trị lượng giác của góc α, nếu:

a)    $\sin \alpha  = \frac{5}{{13}}$ và $\frac{\pi }{2} < \alpha  < \pi $

b)    $\cos \alpha  = \frac{2}{5}$ và $0 < \alpha  < 90^\circ $

c)    $\tan \alpha  = \sqrt 3 $ và $\pi  < \alpha  < \frac{{3\pi }}{2}$

d) $\cot \alpha = -\frac{1}{2}$ và $270^\circ < \alpha < 360^\circ $

Lời giải

a) Ta có: ${\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow {\left( {\frac{5}{{13}}} \right)^2} + {\cos ^2}\alpha = 1 \Rightarrow \cos \alpha = \pm \frac{{12}}{{13}}$

Thực hiện $\frac{\pi }{2} < \alpha < \pi \Rightarrow \cos \alpha = \frac{-{12}}{{13}}$$ \Rightarrow \left\{ \begin{array}{l}\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{-5}{{12}}\\\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{-{12}}{5}\end{array} \right.$

b) Ta có: ${\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Rightarrow {\left( {\frac{2}{5}} \right)^2} + {\sin ^2}\alpha = 1 \Rightarrow \sin \alpha = \pm \frac{{\sqrt {21} }}{5}$

Thực hiện $0 < \alpha < 90^\circ \Rightarrow \sin \alpha = \frac{{\sqrt {21} }}{5}$$ \Rightarrow \left\{ \begin{array}{l}\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{\sqrt {21} }}{2}\\\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{2\sqrt {21} }}{{21}}\end{array} \right.$

c) Ta có: $1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }} \Rightarrow 1 + {\left( {\sqrt 3 } \right)^2} = \frac{1}{{{{\cos }^2}\alpha }} \Rightarrow \cos \alpha = \pm \frac{1}{2}$

Thực hiện $\pi < \alpha < \frac{{3\pi }}{2} \Rightarrow \cos \alpha = \frac{-1}{2}$ $ \Rightarrow \left\{ \begin{array}{l}\cot \alpha .\tan \alpha = 1\\\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\cot \alpha = \frac{{\sqrt 3 }}{3}\\\sin \alpha = \frac{{-\sqrt 3 }}{2}\end{array} \right.$

d) Ta có: $1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }} \Rightarrow 1 + {\left( -{\frac{1}{2}} \right)^2} = \frac{1}{{{{\sin }^2}\alpha }} \Rightarrow \sin \alpha = \pm \frac{{2\sqrt 5 }}{5}$

Thực hiện $270^\circ < \alpha < 360^\circ \Rightarrow \sin \alpha = \frac{{-2\sqrt 5 }}{5}.$

Ta có: $\cot \alpha  = -\frac{1}{2} \Rightarrow \tan \alpha  = \frac{1}{{\cot \alpha }} = -2$

Lại có:

$1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }} \Leftrightarrow 1 + 4 = \frac{1}{{{{\cos }^2}\alpha }}$$ \Leftrightarrow {\cos ^2}\alpha = \frac{1}{5} \Leftrightarrow \cos \alpha = \pm \frac{{\sqrt 5 }}{5}$

Thực hiện ${270^o} < \alpha < {360^o} \Rightarrow \cos \alpha > 0 \Rightarrow \cos \alpha = \frac{{\sqrt 5 }}{5}$

Giải bài 4 trang 19 Toán 11 tập 1

Biểu diễn các giá trị lượng giác sau qua giá trị lượng giác của góc có số đo từ 0 đến $\frac{\pi }{4}$ hoặc từ 0 đến $45^\circ $ và tính

a) $\cos \frac{{31\pi }}{6}$

b) $\sin \frac{{129\pi }}{4}$

c) $\tan 1020^\circ $

Lời giải

a) $\cos \frac{{31\pi }}{6} = \cos \left( {5\pi + \frac{\pi }{6}} \right) = \cos \left( {\pi + \frac{\pi }{6}} \right) = – \cos \left( {\frac{\pi }{6}} \right) = -\frac{{\sqrt3}}{2}$

b) $\sin \frac{{129\pi }}{4} = \sin \left( {32\pi + \frac{\pi }{4}} \right) = \sin \left( {\frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2}$

c) $\tan 1020^\circ = \tan \left( {5.180^\circ + 120^\circ } \right) = \tan \left( {120^\circ} \right) = – \sqrt 3 $

Giải bài 5 trang 19 Toán 11 tập 1

Chứng minh các đẳng thức lượng giác sau:

a) ${\sin ^4}\alpha – {\cos ^4}\alpha = 1 – 2{\cos ^2}\alpha $

b) $\tan \alpha + \cot \alpha = \frac{1}{{\sin \alpha .\cos \alpha }}$

Lời giải

a)    Ta có:

$\begin{array}{l}{\sin ^4}\alpha – {\cos ^4}\alpha = 1 – 2{\cos ^2}\alpha \\ \Trái phải mũi tên \trái( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \phải)\trái( {{{\sin }^2}\alpha – {{\cos }^2}\alpha } \phải) = 1 – 2{\cos ^2}\alpha \\ \Trái phải mũi tên {\sin ^2}\alpha – {\cos ^2}\alpha – 1 + 2{\cos ^2}\alpha = 0\\ \Trái phải mũi tên {\sin ^2}\alpha + {\cos ^2}\alpha – 1 = 0\\ \Trái phải mũi tên 1 – 1 = 0\\ \Trái phải mũi tên 0 = 0\end{mảng}$

Đẳng thức luôn đúng.

b)    Ta có:

$\begin{array}{l}\tan \alpha + \cot \alpha = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{{\sin \alpha }}{{\cos \alpha }} + \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{\cos \alpha .\sin \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\\ \Leftrightarrow \frac{1}{{\sin \alpha .\cos \alpha }} = \frac{1}{{\sin \alpha .\cos \alpha }}\end{mảng}$

Đẳng thức luôn đúng.

Giải bài 6 trang 19 Toán 11 tập 1

Rút gọn các biểu thức sau:

a) $\frac{1}{{\tan \alpha + 1}} + \frac{1}{{\cot \alpha + 1}}$

b) $\cos \left( {\frac{\pi }{2} – \alpha } \right) – \sin \left( {\pi + \alpha } \right)$

c) $\sin \left( {\alpha – \frac{\pi }{2}} \right) + \cos \left( { – \alpha + 6\pi } \right) – \tan \left( {\alpha + \pi } \right)\cot \left( {3\pi – \alpha } \right)$

Lời giải

Một)   

$\begin{array}{l}\frac{1}{{\tan \alpha + 1}} + \frac{1}{{\cot \alpha + 1}} = \frac{{\cot \alpha + 1 + \tan \alpha + 1}}{{\left( {\tan \alpha + 1} \right)\left( {\cot \alpha + 1} \right)}}\\ = \frac{{\tan \alpha + \cot \alpha + 2}}{{\tan \alpha .\cot \alpha + \tan \alpha + \cot \alpha + 1}} = \frac{{\tan \alpha + \cot \alpha + 2}}{{\tan \alpha + \cot \alpha + 2}} = 1\end{array}$

b) $\cos \left( {\frac{\pi }{2} – \alpha } \right) – \sin \left( {\pi + \alpha } \right) = \sin \alpha + \sin \alpha = 2\sin \alpha $

c) $\begin{array}{l}\sin \left( {\alpha – \frac{\pi }{2}} \right) + \cos \left( { – \alpha + 6\pi } \right) – \tan \left( {\alpha + \pi } \right)\cot \left( {3\pi – \alpha } \right)\\ = – \sin \left( {\frac{\pi }{2} – \alpha } \right) + \cos \left( \alpha \right) – \tan \alpha .\cot \left( {\pi – \alpha } \right)\\ = – \cos \alpha + \cos \alpha + \tan \alpha .\cot \alpha \\ = 1\end{array}$

Giải Toán 11 tập 1 trang 20

Giải bài 7 trang 20 Toán 11 tập 1

Thanh OM quay ngược chiều kim đồng hồ quanh trục O của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc xuống mặt đất như Hình 12. Vị trí ban đầu của thanh là OA. Hỏi độ dài bóng O’M’ của OM khi thanh quay được $3\frac{1}{{10}}$ vòng là bao nhiêu, biết thanh độ dài OM là 15cm? Kết quả làm trong đến hàng phần mười.

Lời giải

Đặt hệ trục tọa độ như hình:

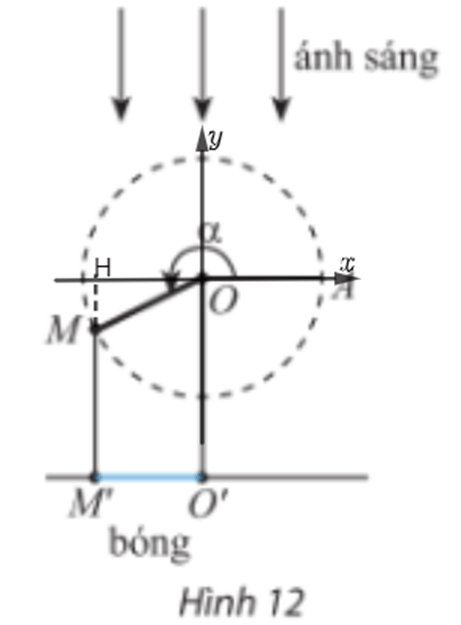
Thanh OM quay được $3\frac{1}{{10}}$ $ \Rightarrow \alpha  = 3\frac{1}{{10}}.360^\circ  = 1116^\circ $.

Kẻ MH vuông góc Ox, H thuộc Ox.

Khi đó $\begin{array}{l}M\left( {15.\cos 1116^\circ ;15.\sin 1116^\circ } \right)\\ \Rightarrow OH = \left| {\cos 1116^\circ } \right|.15 \approx 12,1\end{array}$.

Vậy độ dài bóng O’M’ của OM khi thanh quay được $3\frac{1}{{10}}$ là 12,1cm.

Giải bài 8 trang 20 Toán 11 tập 1

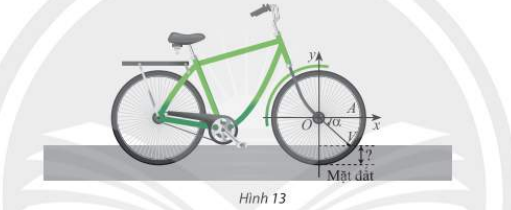
Khi xe đạp di chuyển, van V của bánh xe quay quanh trục O theo chiều kim đồng hồ với tốc độ góc không đổi là 11 rad/s (Hình 13). Ban đầu van nằm ở vị trí A. Hỏi sau một phút di chuyển, khoảng cách từ van đến mặt đất là bao nhiêu, biết bán kính OA = 58cm? Giả sử độ dày của lốp xe không đáng kể. Kết quả làm trong đến hàng phần mười.

Lời giải

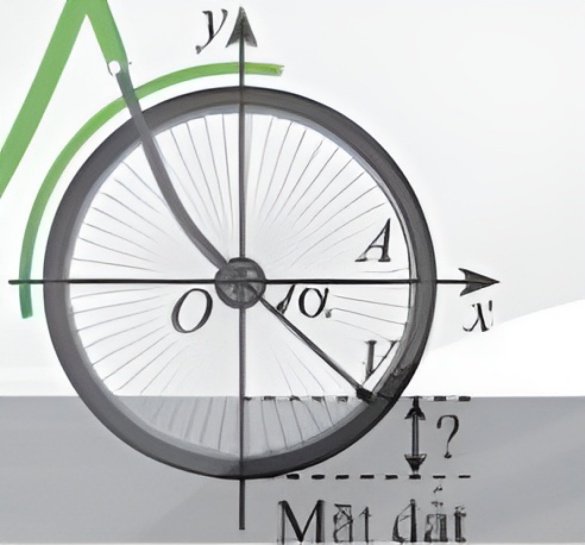
Sau một phút di chuyển, van V đã quay được một góc lượng giác có số đo góc là: $\alpha  = 11.60 = 660\left( {rad} \right)$

Khi đó, tọa độ điểm V biểu diễn cho góc lượng giác trên có tọa độ là: $V\left( {58.\cos \alpha ,58.\sin \alpha } \right) \approx \left( {56;15,2} \right)$

Khi đó khoảng cách từ van đến mặt đất khoảng $58 – 15,2 \approx 42,8\left( {cm} \right)$