Giải Toán 11 tập 1 trang 69 Bài 1:Giới hạn của dãy số
Giải Toán 11 tập 1 trang 69 Bài 1:Giới hạn của dãy số
Giải toán 11 tập 1 trang 69 Bài 1 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 11 Chân trời sáng tạo. Mời các em học sinh cùng quý phụ huynh tham khảo.
Giải Toán 11 tập 1 trang 64
Hoạt động 1 trang 64 Toán 11 tập 1
Cho dãy số $\left( {{u_n}} \right)$ với .${u_n} = \frac{{{{\left( { – 1} \right)}^n}}}{n}$.
a) Tìm các giá trị còn thiếu trong bảng sau:
| n | 10 | 20 | 50 | 100 | 1 000 |
| |un| | 0,1 | 0,05 | 0,02 | ? | ? |
b) Với $n$ thế nào thì $\left| {{u_n}} \right|$ bé hơn 0,01; 0,001?
c) Một số số hạng của dãy số được biểu diễn trên trục số như Hình 1.

Từ các kết quả trên, có nhận xét gì về khoảng cách từ điểm ${u_n}$ đến điểm 0 khi $n$ trở nên rất lớn?
Lời giải:
a) $n = 100 \Leftrightarrow \left| {{u_{100}}} \right| = \left| {\frac{{{{\left( { – 1} \right)}^{100}}}}{{100}}} \right| = \frac{1}{{100}} = 0,01$
$n = 1000 \Leftrightarrow \left| {{u_{1000}}} \right| = \left| {\frac{{{{\left( { – 1} \right)}^{1000}}}}{{1000}}} \right| = \frac{1}{{1000}} = 0,001$
Như vậy ta có thể điền vào bảng như sau:
| n | 10 | 20 | 50 | 100 | 1 000 |
| |un| | 0,1 | 0,05 | 0,02 | 0,01 | 0,001 |
b) Với n > 100 thì |un| < 0,01.
Với n > 1000 thì |un| < 0,001.
b) $\left| {{u_n}} \right| < 0,01 \Leftrightarrow \left| {\frac{{{{\left( { – 1} \right)}^n}}}{n}} \right| < 0,01 \Leftrightarrow \frac{1}{n} < 0,01 \Leftrightarrow n > 100$
Vậy $\left| {{u_n}} \right| < 0,01$ khi $n > 100$.
$\left| {{u_n}} \right| < 0,001 \Leftrightarrow \left| {\frac{{{{\left( { – 1} \right)}^n}}}{n}} \right| < 0,001 \Leftrightarrow \frac{1}{n} < 0,001 \Leftrightarrow n > 1000$
Vậy $\left| {{u_n}} \right| < 0,001$ khi $n > 1000$.
c) Dựa vào trục số ta thấy, khoảng cách từ điểm ${u_n}$ đến điểm 0 trở nên rất bé khi $n$ trở nên rất lớn.
Giải Toán 11 tập 1 trang 65
Thực hành 1 trang 65 Toán 11 tập 1
Tính các giới hạn sau:
a) $\lim \frac{1}{{{n^2}}}$;
b) $\lim {\left( { – \frac{3}{4}} \right)^n}$.
Lời giải:
a) Áp dụng công thức giới hạn cơ bản với $k = 2$, ta có: $\lim \frac{1}{{{n^2}}}$.
b) Do $\left| { – \frac{3}{4}} \right| = \frac{3}{4} < 1$ nên $\lim {\left( { – \frac{3}{4}} \right)^n} = 0$.
Hoạt động 2 trang 65 Toán 11 tập 1
Cho dãy số $\left( {{u_n}} \right)$ với ${u_n} = \frac{{2n + 1}}{n}$.
a) Cho dãy số $\left( {{v_n}} \right)$ với ${v_n} = {u_n} – 2$. Tìm giới hạn $\lim {v_n}$.
b) Biểu diễn các điểm ${u_1},{u_2},{u_3},{u_4}$ trên trục số. Có nhận xét gì về vị trí của các điểm ${u_n}$ khi $n$ trở nên rất lớn?
Lời giải:
a) ${v_n} = {u_n} – 2 = \frac{{2n + 1}}{n} – 2 = \frac{{2n + 1 – 2n}}{n} = \frac{1}{n}$.
Áp dụng giới hạn cơ bản với $k = 1$, ta có: $\lim {v_n} = \lim \frac{1}{n} = 0$.
b) ${u_1} = \frac{{2.1 + 1}}{1} = 3,{u_2} = \frac{{2.2 + 1}}{2} = \frac{5}{2},{u_3} = \frac{{2.3 + 1}}{3} = \frac{7}{3},{u_4} = \frac{{2.4 + 1}}{4} = \frac{9}{4}$
Biểu diễn trên trục số:
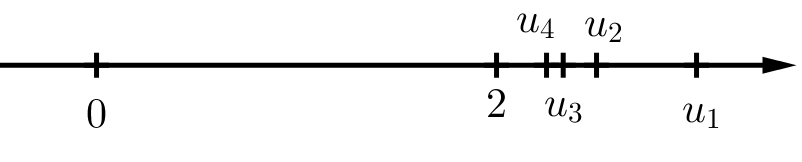
Nhận xét: Điểm ${u_n}$ càng dần đến điểm 2 khi $n$ trở nên rất lớn.
Thực hành 2 trang 65 Toán 11 tập 1
Tìm các giới hạn sau:
a) $\lim \left( {2 + {{\left( {\frac{2}{3}} \right)}^n}} \right)$;
b) $\lim \left( {\frac{{1 – 4n}}{n}} \right)$.
Lời giải:
a) Đặt ${u_n} = 2 + {\left( {\frac{2}{3}} \right)^n} \Leftrightarrow {u_n} – 2 = {\left( {\frac{2}{3}} \right)^n}$.
Suy ra $\lim \left( {{u_n} – 2} \right) = \lim {\left( {\frac{2}{3}} \right)^n} = 0$
Theo định nghĩa, ta có $\lim {u_n} = 2$. Vậy $\lim \left( {2 + {{\left( {\frac{2}{3}} \right)}^n}} \right) = 2$
b) Đặt ${u_n} = \frac{{1 – 4n}}{n} = \frac{1}{n} – 4 \Leftrightarrow {u_n} – \left( { – 4} \right) = \frac{1}{n}$.
Suy ra $\lim \left( {{u_n} – \left( { – 4} \right)} \right) = \lim \frac{1}{n} = 0$.
Theo định nghĩa, ta có $\lim {u_n} = – 4$. Vậy $\lim \left( {\frac{{1 – 4n}}{n}} \right) = – 4$
Giải Toán 11 tập 1 trang 66
Hoạt động 3 trang 66 Toán 11 tập 1
Ở trên ta đã biết $\lim \left( {3 + \frac{1}{{{n^2}}}} \right) = \lim \frac{{3{n^2} + 1}}{{{n^2}}} = 3$.
a) Tìm các giới hạn $\lim 3$ và $\lim \frac{1}{{{n^2}}}$.
b) Từ đó, nêu nhận xét về $\lim \left( {3 + \frac{1}{{{n^2}}}} \right)$ và $\lim 3 + \lim \frac{1}{{{n^2}}}$.
Lời giải:
a) $\lim 3 = 3$ vì 3 là hằng số.
Áp dụng giới hạn cơ bản với $k = 2$, ta có: $\lim \frac{1}{{{n^2}}} = 0$.
b) $\lim \left( {3 + \frac{1}{{{n^2}}}} \right) = \lim 3 + \lim \frac{1}{{{n^2}}} = 3$
Thực hành 3 trang 66 Toán 11 tập 1
Tìm các giới hạn sau:
a) $\lim \frac{{2{n^2} + 3n}}{{{n^2} + 1}}$
b) $\lim \frac{{\sqrt {4{n^2} + 3} }}{n}$
Lời giải:
a) $\lim \frac{{2{n^2} + 3n}}{{{n^2} + 1}} = \lim \frac{{{n^2}\left( {2 + \frac{{3n}}{{{n^2}}}} \right)}}{{{n^2}\left( {1 + \frac{1}{{{n^2}}}} \right)}} = \lim \frac{{2 + \frac{3}{n}}}{{1 + \frac{1}{{{n^2}}}}} = 2$
b) $\lim \frac{{\sqrt {4{n^2} + 3} }}{n} = \lim \frac{{\sqrt {{n^2}\left( {4 + \frac{3}{{{n^2}}}} \right)} }}{n} = \lim \frac{{n\sqrt {4 + \frac{3}{{{n^2}}}} }}{n} = \lim \sqrt {4 + \frac{3}{{{n^2}}}} = 2$
Giải Toán 11 tập 1 trang 67
Hoạt động 4 trang 67 Toán 11 tập 1
Từ một hình vuông có cạnh bằng 1, tô màu một nửa hình vuông, rồi tô màu một nửa hình còn lại và cứ tiếp tục như vậy (xem Hình 2).
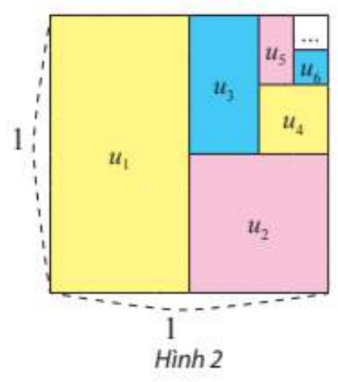
a) Xác định diện tích ${u_k}$ của phần hình được tô màu lần thứ $k\left( {k = 1,2,3,…} \right)$.
b) Tính tổng diện tính ${S_n}$ của phần hình được tô màu sau lần tô thứ $n\left( {n = 1,2,3,…} \right)$.
c) Tìm giới hạn $\lim {S_n}$ và so sánh giới hạn này với diện tích hình vuông ban đầu.
Lời giải:
a) Theo đề bài, ta thấy $\left( {{u_k}} \right)$ là cấp số nhân với số hạng đầu ${u_1} = \frac{1}{2}$, công bội $q = \frac{1}{2}$.
Vậy ${u_k} = {u_1}.{q^{k – 1}} = \frac{1}{2}.{\left( {\frac{1}{2}} \right)^{k – 1}} = {\left( {\frac{1}{2}} \right)^k} = \frac{1}{{{2^k}}}$.
b) $\left( {{u_n}} \right)$ là cấp số nhân với số hạng đầu ${u_1} = \frac{1}{2}$, công bội $q = \frac{1}{2}$.
Vậy ${S_n} = {u_1}.\frac{{1 – {q^n}}}{{1 – q}} = \frac{1}{2}.\frac{{1 – {{\left( {\frac{1}{2}} \right)}^n}}}{{1 – \frac{1}{2}}} = \frac{1}{2}.\frac{{1 – {{\left( {\frac{1}{2}} \right)}^n}}}{{\frac{1}{2}}} = 1 – {\left( {\frac{1}{2}} \right)^n}$.
c) $\lim {S_n} = \lim \left( {1 – {{\left( {\frac{1}{2}} \right)}^n}} \right) = \lim 1 – \lim {\left( {\frac{1}{2}} \right)^n}$.
$\lim 1 = 1$ vì 1 là hằng số.
$\left| {\frac{1}{2}} \right| = \frac{1}{2} < 1$ nên $\lim {\left( {\frac{1}{2}} \right)^n} = 0$
Vậy $\lim {S_n} = \lim 1 – \lim {\left( {\frac{1}{2}} \right)^n} = 1 – 0 = 1$
Giới hạn này bằng diện tích của hình vuông ban đầu.
Giải Toán 11 tập 1 trang 68
Thực hành 4 trang 68 Toán 11 tập 1
Tính tổng của cấp số nhân lùi vô hạn: $1 + \frac{1}{3} + {\left( {\frac{1}{3}} \right)^2} + … + {\left( {\frac{1}{3}} \right)^n} + …$.
Lời giải:
Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu ${u_1} = 1$ và công bội $q = \frac{1}{3}$ nên
$1 + \frac{1}{3} + {\left( {\frac{1}{3}} \right)^2} + … + {\left( {\frac{1}{3}} \right)^n} + … = \frac{1}{{1 – \frac{1}{3}}} = \frac{3}{2}$.
Vận dụng 1 trang 68 Toán 11 tập 1
Từ tờ giấy, cắt một hình tròn bán kính $R\left( {cm} \right)$ như Hình 3a. Tiếp theo, cắt hai hình tròn bán kính $\frac{R}{2}$ rồi chồng lên hình tròn đầu tiên như Hình 3b. Tiếp theo, cắt bốn hình tròn bán kính $\frac{R}{4}$ rồi chồng lên các hình trước như Hình 3c. Cứ thế tiếp tục mãi. Tính tổng diện tích của các hình tròn.
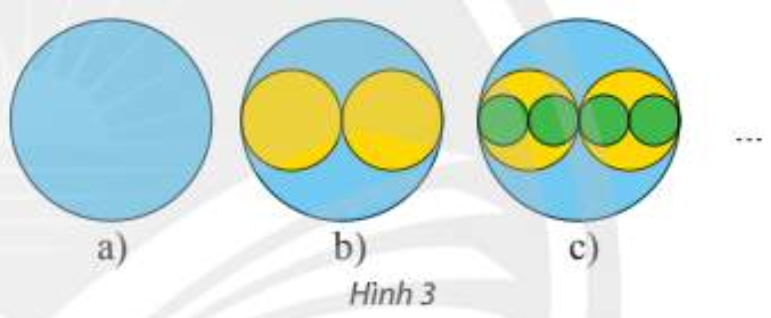
Lời giải:
Giả sử các hình tròn bán kính ${R_1} = R,{R_2} = \frac{R}{2},{R_3} = \frac{R}{4} = \frac{R}{{{2^2}}},…,{R_n} = \frac{R}{{{2^{n – 1}}}},…$ có diện tích lần lượt là ${u_1},{u_2},{u_3},…,{u_n},…$ Ta có:
$\begin{array}{l}{u_1} = \pi R_1^2 = \pi {R^2},{u_2} = \pi R_2^2 = \pi {\left( {\frac{R}{2}} \right)^2} = \pi {R^2}.\frac{1}{{{2^2}}},{u_3} = \pi R_3^2 = \pi {\left( {\frac{R}{{{2^2}}}} \right)^2} = \pi {R^2}.\frac{1}{{{2^4}}},…,\\{u_n} = \pi R_n^2 = \pi {\left( {\frac{R}{{{2^{n – 1}}}}} \right)^2} = \pi {R^2}.\frac{1}{{{2^{2n – 2}}}},…\end{array}$
$\begin{array}{l}S = {u_1} + {u_2} + … + {u_n} + … = \pi {R^2} + 2\pi {R^2}.\frac{1}{{{2^2}}} + 4.\pi {R^2}.\frac{1}{{{2^4}}} + … + {2^{n + 1}}\pi {R^2}.\frac{1}{{{2^{2n – 2}}}} + …\\\,\,\,\, = \pi {R^2} + \pi {R^2}.\frac{1}{2} + \pi {R^2}.\frac{1}{{{2^2}}} + … + \pi {R^2}.\frac{1}{{{2^{n – 1}}}} + …\\\,\,\,\, = \pi {R^2}\left( {1 + \frac{1}{2} + \frac{1}{{{2^2}}} + … + \frac{1}{{{2^{n – 1}}}} + …} \right)\end{array}$
Xét tổng: ${S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + … + \frac{1}{{{2^{n – 1}}}} + …$
Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu ${u_1} = 1$ và công bội $q = \frac{1}{2}$ nên: ${S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + … + \frac{1}{{{2^{n – 1}}}} + … = \frac{1}{{1 – \frac{1}{2}}} = 2$.
Vậy $S = \pi {R^2}.{S_n} = 2\pi {R^2}$.
Hoạt động 5 trang 68 Toán 11 tập 1
Dựng một dãy hình vuông bằng cách ghép từ các hình vuông đơn vị (cạnh bằng 1 đơn vị độ dài) theo các bước như Hình 4. Kí hiệu ${u_n}$ (đơn vị diện tích) là diện tích hình vuông dựng được ở bước thứ $n$.
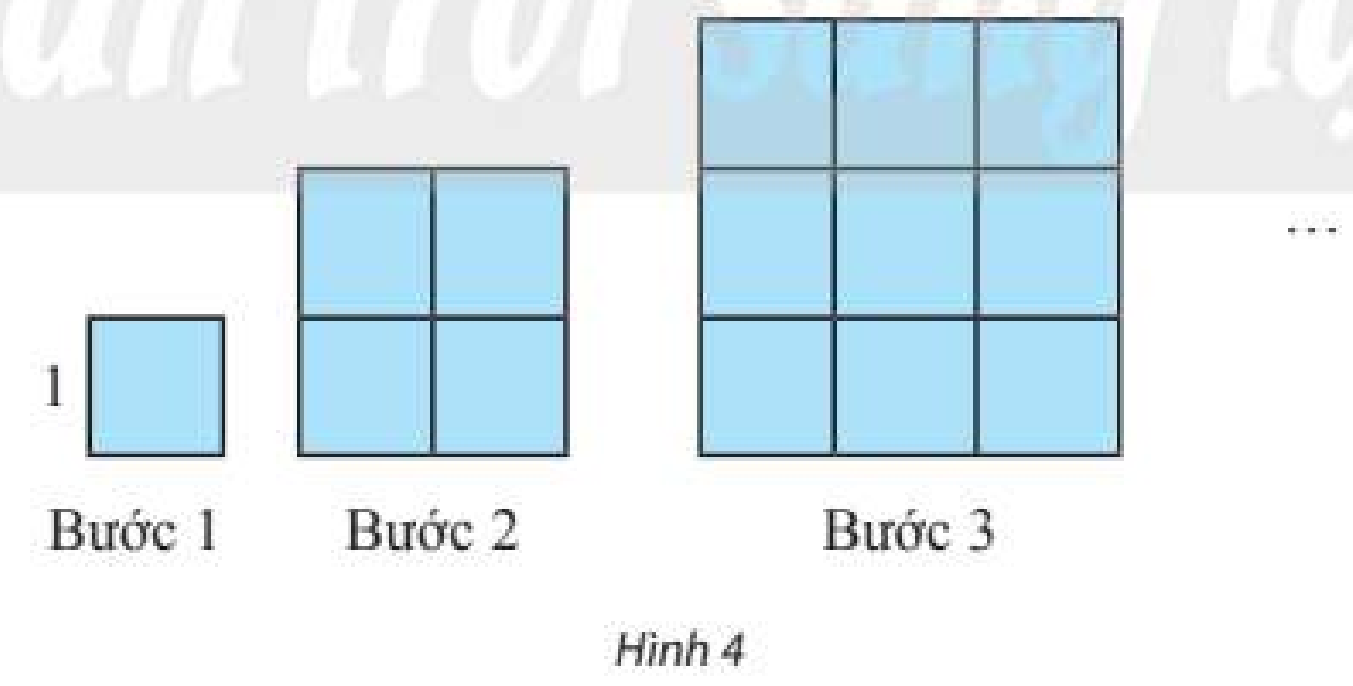
a) Với $n$ như thế nào thì ${u_n}$ vượt quá 10000; 1000000?
b) Cho hình có diện tích $S$. Với $n$ như thế nào thì ${u_n}$ vượt quá $S$?
Lời giải:
a) Ta có: ${u_1} = {1^2};{u_2} = {2^2};{u_3} = {3^2};…;{u_n} = {n^2}$
$\begin{array}{l}{u_n} > 10000 \Leftrightarrow {n^2} > 10000 = {100^2} \Leftrightarrow n > 100\\{u_n} > 1000000 \Leftrightarrow {n^2} > 1000000 = {1000^2} \Leftrightarrow n > 1000\end{array}$
b) ${u_n} > S \Leftrightarrow {n^2} > S \Leftrightarrow n > \sqrt S $.
Vậy với các số tự nhiên $n > \sqrt S $ thì ${u_n} > S$.
Giải Toán 11 tập 1 trang 69
Giải bài 1 trang 69 Toán 11 tập 1
Tìm các giới hạn sau:
a) $\lim \frac{{ – 2n + 1}}{n}$
b) $\lim \frac{{\sqrt {16{n^2} – 2} }}{n}$
c) $\lim \frac{4}{{2n + 1}}$
d) $\lim \frac{{{n^2} – 2n + 3}}{{2{n^2}}}$
Lời giải
a) $\lim \frac{{ – 2n + 1}}{n} = \lim \frac{{n\left( { – 2 + \frac{1}{n}} \right)}}{n} = \lim \left( { – 2 + \frac{1}{n}} \right) = – 2$
b) $\lim \frac{{\sqrt {16{n^2} – 2} }}{n} = \lim \frac{{\sqrt {{n^2}\left( {16 – \frac{2}{{{n^2}}}} \right)} }}{n} = \lim \frac{{n\sqrt {16 – \frac{2}{{{n^2}}}} }}{n} = \lim \sqrt {16 – \frac{2}{{{n^2}}}} = 4$
c) $\lim \frac{4}{{2n + 1}} = \lim \frac{4}{{n\left( {2 + \frac{1}{n}} \right)}} = \lim \left( {\frac{4}{n}.\frac{1}{{2 + \frac{1}{n}}}} \right) = \lim \frac{4}{n}.\lim \frac{1}{{2 + \frac{1}{n}}} = 0$
d) $\lim \frac{{{n^2} – 2n + 3}}{{2{n^2}}} = \lim \frac{{{n^2}\left( {1 – \frac{2}{n} + \frac{3}{{{n^2}}}} \right)}}{{2{n^2}}} = \lim \frac{{1 – \frac{2}{n} + \frac{3}{{{n^2}}}}}{2} = \frac{1}{2}$
Giải bài 2 trang 69 Toán 11 tập 1
Tính tổng của các cấp số nhân lùi vô hạn sau:
a) $ – \frac{1}{2} + \frac{1}{4} – \frac{1}{8} + … + {\left( { – \frac{1}{2}} \right)^n} + …$
b) $\frac{1}{4} + \frac{1}{{16}} + \frac{1}{{64}} + … + {\left( {\frac{1}{4}} \right)^n} + …$
Lời giải
a) $ – \frac{1}{2} + \frac{1}{4} – \frac{1}{8} + … + {\left( { – \frac{1}{2}} \right)^n} + …$
Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu ${u_1} = – \frac{1}{2}$ và công bội $q = – \frac{1}{2}$ nên: $ – \frac{1}{2} + \frac{1}{4} – \frac{1}{8} + … + {\left( { – \frac{1}{2}} \right)^n} + … = \frac{{ – \frac{1}{2}}}{{1 – \left( { – \frac{1}{2}} \right)}} = – \frac{1}{3}$
b) $\frac{1}{4} + \frac{1}{{16}} + \frac{1}{{64}} + … + {\left( {\frac{1}{4}} \right)^n} + …$
Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu ${u_1} = \frac{1}{4}$ và công bội $q = \frac{1}{4}$ nên: $\frac{1}{4} + \frac{1}{{16}} + \frac{1}{{64}} + … + {\left( {\frac{1}{4}} \right)^n} + … = \frac{{\frac{1}{4}}}{{1 – \frac{1}{4}}} = \frac{1}{3}$
Giải bài 3 trang 69 Toán 11 tập 1
Viết số thập phân vô hạn tuần hoàn $0,444…$ dưới dạng một phân số.
Lời giải
$0,444… = 0,4 + 0,04 + 0,004 + …$
Số $0,444…$ là tổng của cấp số nhân lùi vô hạn có số hạng đầu bằng $0,4$ và công bội bằng $\frac{1}{{10}}$.
Do đó: $0,444… = \frac{{0,4}}{{1 – \frac{1}{{10}}}} = \frac{4}{9}$
Giải Toán 11 tập 1 trang 70
Giải bài 4 trang 70 Toán 11 tập 1
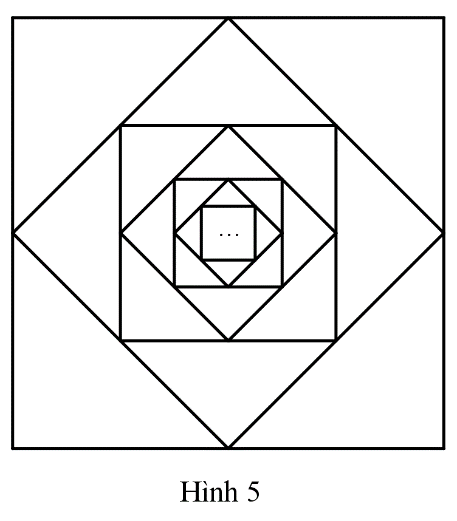
Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dài), nối các trung điểm của bốn cạnh để có hình vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của hình vuông thứ hai để được hình vuông thứ ba. Cứ tiếp tục làm như thế, nhận được một dãy hình vuông (xem Hình 5).
a) Kí hiệu ${a_n}$ là diện tích của hình vuông thứ $n$ và ${S_n}$ là tổng diện tích của $n$ hình vuông đầu tiên. Viết công thức tính ${a_n},{S_n}\left( {n = 1,2,3,…} \right)$ và tìm $\lim {S_n}$ (giới hạn này nếu có được gọi là tổng diện tích của các hình vuông).
b) Kí hiệu ${p_n}$ là chu vi của hình vuông thứ $n$ và ${Q_n}$ là tổng chu vi của $n$ hình vuông đầu tiên. Viết công thức tính ${p_n}$ và ${Q_n}\left( {n = 1,2,3,…} \right)$ và tìm $\lim {Q_n}$ (giới hạn này nếu có được gọi là tổng chu vi của các hình vuông).
Lời giải
a) Gọi ${u_n}$ là độ dài cạnh của hình vuông thứ n.
Đường chéo của hình vuông thứ n có độ dài là ${u_n}\sqrt 2 $.
Độ dài cạnh hình vuông thứ n + 1 bằng nửa độ dài đường chéo hình vuông thứ n nên ta có:
${u_{n + 1}} = \frac{{{u_n}\sqrt 2 }}{2} = {u_n}.\frac{1}{{\sqrt 2 }}$.
Từ đó ta thấy $\left( {{u_n}} \right)$ là một cấp số nhân có số hạng đầu ${u_1} = 1$, công bội $q = \frac{1}{{\sqrt 2 }}$.
Vậy ${u_n} = {u_1}.{q^{n – 1}} = 1.{\left( {\frac{1}{{\sqrt 2 }}} \right)^{n – 1}} = \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n – 1}}}},n = 1,2,3,…$
Diện tích của hình vuông thứ $n$ là: ${a_n} = u_n^2 = {\left( {\frac{1}{{{{\left( {\sqrt 2 } \right)}^{n – 1}}}}} \right)^2} = \frac{1}{{{2^{n – 1}}}},n = 1,2,3,…$
Vậy ${S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + … + \frac{1}{{{2^{n – 1}}}}$
Đây là tổng của cấp số nhân có số hạng đầu ${u_1} = 1$, công bội $q = \frac{1}{2}$.
Vậy ${S_n} = 1.\frac{{1 – {{\left( {\frac{1}{2}} \right)}^n}}}{{1 – \frac{1}{2}}} = 2\left( {1 – \frac{1}{{{2^n}}}} \right)$.
$\lim {S_n} = \lim 2\left( {1 – \frac{1}{{{2^n}}}} \right) = 2\left( {1 – \lim \frac{1}{{{2^n}}}} \right) = 2\left( {1 – 0} \right) = 2$.
b) Chu vi của hình vuông thứ $n$ là: ${p_n} = 4{u_n} = 4.\frac{1}{{{{\left( {\sqrt 2 } \right)}^{n – 1}}}} = \frac{4}{{{{\left( {\sqrt 2 } \right)}^{n – 1}}}},n = 1,2,3,…$
Vậy ${Q_n} = 4 + \frac{4}{{\sqrt 2 }} + \frac{4}{{{{\left( {\sqrt 2 } \right)}^2}}} + … + \frac{4}{{{{\left( {\sqrt 2 } \right)}^{n – 1}}}} = 4\left( {1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + … + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n – 1}}}}} \right)$
$1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + … + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n – 1}}}}$ là tổng của cấp số nhân có số hạng đầu ${u_1} = 1$, công bội $q = \frac{1}{{\sqrt 2 }}$.
Vậy $1 + \frac{1}{{\sqrt 2 }} + \frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + … + \frac{1}{{{{\left( {\sqrt 2 } \right)}^{n – 1}}}} = 1.\frac{{1 – {{\left( {\frac{1}{{\sqrt 2 }}} \right)}^n}}}{{1 – \frac{1}{{\sqrt 2 }}}} = \left( {2 + \sqrt 2 } \right)\left( {1 – \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)$.
$ \Rightarrow {Q_n} = 4\left( {2 + \sqrt 2 } \right)\left( {1 – \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)$
$\begin{array}{l}\lim {Q_n} = \lim 4\left( {2 + \sqrt 2 } \right)\left( {1 – \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right) = 4\left( {2 + \sqrt 2 } \right)\left( {1 – \lim \frac{1}{{{{\left( {\sqrt 2 } \right)}^n}}}} \right)\\ = 4\left( {2 + \sqrt 2 } \right)\left( {1 – 0} \right) = 4\left( {2 + \sqrt 2 } \right)\end{array}$.
Giải bài 5 trang 70 Toán 11 tập 1
Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau:
Bắt đầu bằng một hình vuông ${H_0}$ cạnh bằng 1 đơn vị độ dài (xem Hình 6a). Chia hình vuông ${H_0}$ thành chính hình vuông bằng nhau, bỏ đi bốn hình vuông, nhận được hình ${H_1}$ (xem Hình 6b). Tiếp theo, chia mỗi hình vuông của ${H_1}$ thành chín hình vuông, rồi bỏ đi bốn hình vuông, nhận được hình ${H_2}$ (xem Hình 6c). Tiếp tục quá trình này, ta nhận được một dãy hình ${H_n}\left( {n = 1,2,3,…} \right)$.
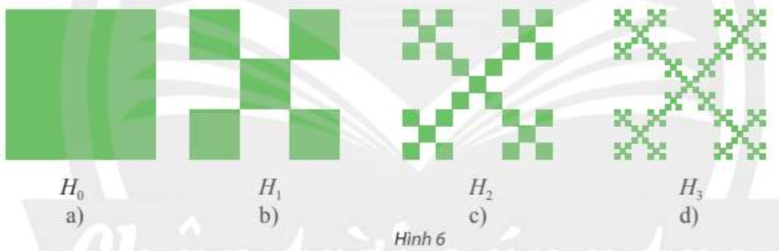
Ta có: ${H_1}$ có 5 hình vuông, mỗi hình vuông có cạnh bằng $\frac{1}{3}$;
${H_2}$ có $5.5 = {5^2}$ hình vuông, mỗi hình vuông có cạnh bằng $\frac{1}{3}.\frac{1}{3} = \frac{1}{{{3^2}}}$;…
Từ đó, nhận được hình ${H_n}$ có ${5^n}$ hình vuông, mỗi hình vuông có cạnh bằng $\frac{1}{{{3^n}}}$.
a) Tính diện tích ${S_n}$ của ${H_n}$ và tính $\lim {S_n}$.
b) Tính chu vi ${p_n}$ của ${H_n}$ và tính $\lim {p_n}$.
(Quá trình trên tạo nên một hình, gọi là một fractal, được coi là có diện tích $\lim {S_n}$ và chu vi $\lim {p_n}$).
Lời giải
a) Ta có:
Diện tích ${H_1}$ bằng $5.{\left( {\frac{1}{3}} \right)^2}$;
Diện tích ${H_2}$ bằng ${5^2}.{\left( {{{\left( {\frac{1}{3}} \right)}^2}} \right)^2} = {5^2}.{\left( {\frac{1}{{{3^2}}}} \right)^2}$;
Diện tích ${H_3}$ bằng ${5^3}.{\left( {{{\left( {\frac{1}{3}} \right)}^3}} \right)^2} = {5^3}.{\left( {\frac{1}{{{3^3}}}} \right)^2}$;…
Diện tích ${H_n}$ bằng ${5^n}.{\left( {\frac{1}{{{3^n}}}} \right)^2}$.
${S_n} = {5^n}.{\left( {\frac{1}{{{3^n}}}} \right)^2} = {5^n}.\frac{1}{{{9^n}}} = {\left( {\frac{5}{9}} \right)^n},n = 1,2,3,…$
$\lim {S_n} = \lim {\left( {\frac{5}{9}} \right)^n} = 0$
b) Ta có:
Chu vi ${H_1}$ bằng $5.4.\frac{1}{3} = 4.\frac{5}{3}$;
Chu vi ${H_2}$ bằng ${5^2}.4.{\left( {\frac{1}{3}} \right)^2} = 4.{\left( {\frac{5}{3}} \right)^2}$;…
Chu vi ${H_n}$ bằng ${5^n}.4.{\left( {\frac{1}{3}} \right)^n} = 4.{\left( {\frac{5}{3}} \right)^n}$.
${p_n} = {5^n}.4.\frac{1}{{{3^n}}} = 4.{\left( {\frac{5}{3}} \right)^n},n = 1,2,3,…$
$\lim {p_n} = \lim \left( {4.{{\left( {\frac{5}{3}} \right)}^n}} \right)$
Vì $\lim \frac{1}{{4.{{\left( {\frac{5}{3}} \right)}^n}}} = \frac{1}{4}.\lim {\left( {\frac{3}{5}} \right)^n} = 0$ và $4.{\left( {\frac{5}{3}} \right)^n} > 0$ với mọi $n$ nên $\lim {p_n} = \lim \left( {4.{{\left( {\frac{5}{3}} \right)}^n}} \right) = + \infty $.
