Giải Toán 11 tập 1 trang 86 Bài tập cuối chương 3

Giải toán 11 tập 1 trang 86 Bài tập cuối chương 3 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 11 Chân trời sáng tạo. Mời các em học sinh cùng quý phụ huynh tham khảo.

Giải Toán 11 tập 1 trang 85

Giải bài 1 trang 85 Toán 11 tập 1

$lim\frac{n+3}{n^{2}}$ bằng

A. 1

B. 0

C. 3

D. 2

Bài làm

$lim\frac{n+3}{n^{2}} = lim\left (\frac{1}{n}+\frac{3}{n^{2}} \right ) =lim\frac{1}{n}+lim\frac{3}{n^{2}}=0+0=0$

Đáp án: B

Giải bài 2 trang 85 Toán 11 tập 1

Tổng của cấp số nhân lùi vô hạn:

$M= 1+\frac{1}{4}+\frac{1}{4^{2}}+…+\frac{1}{4^{n}}+$… bằng

A. $\frac{3}{4}$

B. $\frac{5}{4}$

C. $\frac{4}{3}$

D. $\frac{6}{5}$

Bài làm

$M = \frac{1}{1-\frac{1}{4}}=\frac{4}{3}$

Đáp án: C

Giải bài 3 trang 85 Toán 11 tập 1

$\lim_{x \to 3}\frac{x^{2}-9}{x-3}$ bằng

A: 0

B. 6

C. 3

D. 1

Bài làm

$\lim_{x \to 3}\frac{x^{2}-9}{x-3} = \lim_{x \to 3}\frac{(x+3)(x-3)}{x-3}=\lim_{x \to 3}(x+3)=3+3=6$

Đáp án: B

Giải bài 4 trang 85 Toán 11 tập 1

Hàm số:

$\left\{\begin{matrix}x^{2}+2x+m; x\geq 2\\3; x<2\end{matrix}\right.$ liên tục tại x = 2 khi

A. m = 3

B. m = 5

C. m = -3

D. m = -5

Bài làm

$\lim_{x \to 2^{+}}f(x)= \lim_{x \to 2^{+}}(x^{2}+2x+m)= 2^{2}+2.2+m=m+8$

$\lim_{x \to 2^{-}}f(x)=\lim_{x \to 2^{-}}3= 3$

Để hàm số f(x) liên tục tại x = 2 thì m + 8 = 3 Hay m = -5

Đáp án: D

Giải bài 5 trang 85 Toán 11 tập 1

$\lim_{x \to +\infty}\frac{2x-1}{x}$ bằng:

A. 2

B. -1

C. 0

D. 1

Bài làm

$\lim_{x \to +\infty}\frac{2x-1}{x} = \lim_{x \to +\infty}\left ( 2-\frac{1}{x} \right ) = 2-\lim_{x \to +\infty}\frac{1}{x}=2-0=2$

Đáp án: A

Giải Toán 11 tập 1 trang 86

Giải bài 6 trang 86 Toán 11 tập 1

Tìm các giới hạn sau:

a) $lim\frac{3n-1}{n}$

b) $lim\frac{\sqrt{n^{2}+2}}{n}$

c) $lim\frac{2}{3n+1}$

d) $lim\frac{(n+1)(2n+2)}{n^{2}}$

Bài làm

a) $\lim \frac{{3n – 1}}{n} = \lim \frac{{n\left( {3 – \frac{1}{n}} \right)}}{n} = \lim \left( {3 – \frac{1}{n}} \right) = 3 – 0 = 3$

b) $\lim \frac{{\sqrt {{n^2} + 2} }}{n} = \lim \frac{{\sqrt {{n^2}\left( {1 + \frac{2}{{{n^2}}}} \right)} }}{n} = \lim \frac{{n\sqrt {1 + \frac{2}{{{n^2}}}} }}{n} = \lim \sqrt {1 + \frac{2}{{{n^2}}}}  = 1 + 0 = 1$

c) $\lim \frac{2}{{3n + 1}} = \lim \frac{2}{{n\left( {3 + \frac{1}{n}} \right)}} = \lim \left( {\frac{2}{n}.\frac{1}{{3 + \frac{1}{n}}}} \right) = \lim \frac{2}{n}.\lim \frac{1}{{3 + \frac{1}{n}}} = 0.\frac{1}{{3 + 0}} = 0$

d) $\lim \frac{{\left( {n + 1} \right)\left( {2n + 2} \right)}}{{{n^2}}} = \lim \frac{{n\left( {1 + \frac{1}{n}} \right).2n\left( {1 + \frac{1}{n}} \right)}}{{{n^2}}} = \lim \frac{{2{n^2}{{\left( {1 + \frac{1}{n}} \right)}^2}}}{{{n^2}}}$

$ = \lim 2{\left( {1 + \frac{1}{n}} \right)^2} = 2.{\left( {1 + 0} \right)^2} = 2$

Giải bài 7 trang 86 Toán 11 tập 1

Cho tam giác đều có cạnh bằng a, gọi là tam giác $H_{1}$ . Nối các trung điểm của $H_{1}$ để tạo thành tam giác $H_{2}$. Tiếp theo, nối các trung điểm của $H_{2}$ để tạp thành tam giác $H_{3}$ (Hình 1). Cứ như thế tiếp tục, nhận dược dãy tam giác $H_{1}$, $H_{2}$, $H_{3}$,…

Tính tổng chu vi và tổng diện tích của các tam giác của dãy.

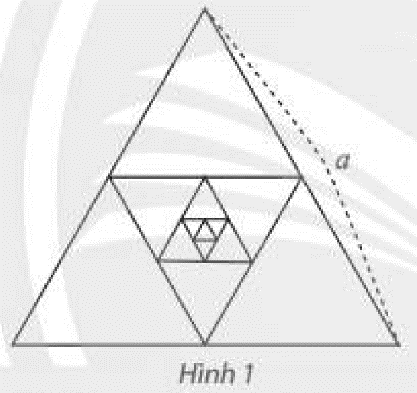
Bài làm

Gọi ${u_n}$ là độ dài cạnh của tam giác đều thứ $n$.

Ta có: ${u_1} = a;{u_2} = \frac{{{u_1}}}{2};{u_3} = \frac{{{u_2}}}{2};…$

Từ đó ta thấy $\left( {{u_n}} \right)$ là một cấp số nhân có số hạng đầu ${u_1} = a$, công bội $q = \frac{1}{2}$.

Vậy ${u_n} = {u_1}.{q^{n – 1}} = a.{\left( {\frac{1}{2}} \right)^{n – 1}} = \frac{a}{{{2^{n – 1}}}},n = 1,2,3,…$

Chu vi của tam giác đều thứ $n$ là: ${p_n} = 3{u_n} = \frac{{3{\rm{a}}}}{{{2^{n – 1}}}},n = 1,2,3,…$

Tổng chu vi của các tam giác của dãy là:

${P_n} = 3{\rm{a}} + \frac{{3{\rm{a}}}}{2} + \frac{{3{\rm{a}}}}{{{2^2}}} + … + \frac{{3{\rm{a}}}}{{{2^{n – 1}}}} + … = 3{\rm{a}}\left( {1 + \frac{1}{2} + \frac{1}{{{2^2}}} + … + \frac{1}{{{2^{n – 1}}}} + …} \right)$

Tổng $1 + \frac{1}{2} + \frac{1}{{{2^2}}} + … + \frac{1}{{{2^{n – 1}}}} + …$ là tổng của cấp số nhân lùi vô hạn có số hạng đầu ${u_1} = 1$, công bội $q = \frac{1}{2}$.

Vậy $1 + \frac{1}{2} + \frac{1}{{{2^2}}} + … + \frac{1}{{{2^{n – 1}}}} + … = \frac{1}{{1 – \frac{1}{2}}} = 2 \Rightarrow {P_n} = 3{\rm{a}}.2 = 6{\rm{a}}$.

Diện tích của hình vuông thứ $n$ là:

${s_n} = \frac{{u_n^2\sqrt 3 }}{4} = {\left( {\frac{a}{{{2^{n – 1}}}}} \right)^2}.\frac{{\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}.{\left( {\frac{1}{{{2^{n – 1}}}}} \right)^2} = \frac{{{a^2}\sqrt 3 }}{4}.\frac{1}{{{4^{n – 1}}}},n = 1,2,3,…$

Tổng diện tích của các tam giác của dãy là:

${S_n} = \frac{{{a^2}\sqrt 3 }}{4} + \frac{{{a^2}\sqrt 3 }}{4}.\frac{1}{4} + \frac{{{a^2}\sqrt 3 }}{4}.\frac{1}{{{4^2}}} + … + \frac{{{a^2}\sqrt 3 }}{4}.\frac{1}{{{4^{n – 1}}}} + … = \frac{{{a^2}\sqrt 3 }}{4}\left( {1 + \frac{1}{4} + \frac{1}{{{4^2}}} + … + \frac{1}{{{4^{n – 1}}}} + …} \right)$

Tổng $1 + \frac{1}{4} + \frac{1}{{{4^2}}} + … + \frac{1}{{{4^{n – 1}}}} + …$ là tổng của cấp số nhân lùi vô hạn có số hạng đầu ${u_1} = 1$, công bội $q = \frac{1}{4}$.

Vậy $1 + \frac{1}{4} + \frac{1}{{{4^2}}} + … + \frac{1}{{{4^{n – 1}}}} + … = \frac{1}{{1 – \frac{1}{4}}} = \frac{4}{3} \Rightarrow {S_n} = \frac{{{a^2}\sqrt 3 }}{4}.\frac{4}{3} = \frac{{{a^2}\sqrt 3 }}{3}$

Giải bài 8 trang 86 Toán 11 tập 1

Tìm các giới hạn sau:

a) $\lim_{x \to -1}(3x^{2}-x+2)$

b) $\lim_{x \to 4}\frac{x^{2}-16}{x-4}$

c) $\lim_{x \to 2}\frac{3-\sqrt{x+7}}{x-2}$

Bài làm

a) $\mathop {\lim }\limits_{x \to  – 1} \left( {3{x^2} – x + 2} \right) = \mathop {\lim }\limits_{x \to  – 1} \left( {3{x^2}} \right) – \mathop {\lim }\limits_{x \to  – 1} x + \mathop {\lim }\limits_{x \to  – 1} 2$

$ = 3\mathop {\lim }\limits_{x \to  – 1} \left( {{x^2}} \right) – \mathop {\lim }\limits_{x \to  – 1} x + \mathop {\lim }\limits_{x \to  – 1} 2 = 3.{\left( { – 1} \right)^2} – \left( { – 1} \right) + 2 = 6$

b) $\mathop {\lim }\limits_{x \to 4} \frac{{{x^2} – 16}}{{x – 4}} = \mathop {\lim }\limits_{x \to 4} \frac{{\left( {x – 4} \right)\left( {x + 4} \right)}}{{x – 4}} = \mathop {\lim }\limits_{x \to 4} \left( {x + 4} \right) = \mathop {\lim }\limits_{x \to 4} x + \mathop {\lim }\limits_{x \to 4} 4 = 4 + 4 = 8$

c) $\mathop {\lim }\limits_{x \to 2} \frac{{3 – \sqrt {x + 7} }}{{x – 2}} = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {3 – \sqrt {x + 7} } \right)\left( {3 + \sqrt {x + 7} } \right)}}{{\left( {x – 2} \right)\left( {3 + \sqrt {x + 7} } \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{{{3^2} – \left( {x + 7} \right)}}{{\left( {x – 2} \right)\left( {3 + \sqrt {x + 7} } \right)}}$

$ = \mathop {\lim }\limits_{x \to 2} \frac{{2 – x}}{{\left( {x – 2} \right)\left( {3 + \sqrt {x + 7} } \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{{ – \left( {x – 2} \right)}}{{\left( {x – 2} \right)\left( {3 + \sqrt {x + 7} } \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{{ – 1}}{{3 + \sqrt {x + 7} }}$

$ = \frac{{\mathop {\lim }\limits_{x \to 2} \left( { – 1} \right)}}{{\mathop {\lim }\limits_{x \to 2} 3 + \sqrt {\mathop {\lim }\limits_{x \to 2} x + \mathop {\lim }\limits_{x \to 2} 7} }} = \frac{{ – 1}}{{3 + \sqrt {2 + 7} }} =  – \frac{1}{6}$

Giải bài 9 trang 86 Toán 11 tập 1

Tìm các giới hạn sau:

a) $\lim_{x \to +\infty}\frac{-x+2}{x+1}$

b) $\lim_{x \to -\infty}\frac{x-2}{x^{2}}$

Bài làm

a) $\mathop {\lim }\limits_{x \to  + \infty } \frac{{ – x + 2}}{{x + 1}} = \mathop {\lim }\limits_{x \to  + \infty } \frac{{x\left( { – 1 + \frac{2}{x}} \right)}}{{x\left( {1 + \frac{1}{x}} \right)}} = \mathop {\lim }\limits_{x \to  + \infty } \frac{{ – 1 + \frac{2}{x}}}{{1 + \frac{1}{x}}} = \frac{{\mathop {\lim }\limits_{x \to  + \infty } \left( { – 1} \right) + \mathop {\lim }\limits_{x \to  + \infty } \frac{2}{x}}}{{\mathop {\lim }\limits_{x \to  + \infty } 1 + \mathop {\lim }\limits_{x \to  + \infty } \frac{1}{x}}} = \frac{{ – 1 + 0}}{{1 + 0}} =  – 1$

b) $\mathop {\lim }\limits_{x \to  – \infty } \frac{{x – 2}}{{{x^2}}} = \mathop {\lim }\limits_{x \to  – \infty } \frac{{x\left( {1 – \frac{2}{x}} \right)}}{{{x^2}}} = \mathop {\lim }\limits_{x \to  – \infty } \frac{1}{x}.\mathop {\lim }\limits_{x \to  – \infty } \left( {1 – \frac{2}{x}} \right)$

$ = \mathop {\lim }\limits_{x \to  – \infty } \frac{1}{x}.\left( {\mathop {\lim }\limits_{x \to  – \infty } 1 – \mathop {\lim }\limits_{x \to  – \infty } \frac{2}{x}} \right) = 0.\left( {1 – 0} \right) = 0$.

Giải bài 10 trang 86 Toán 11 tập 1

Tìm các giới hạn sau:

a) $\lim_{x \to 4^{+}}\frac{1}{x-4}$

b) $\lim_{x \to 2^{+}}\frac{x}{2-x}$

Bài làm

a) Áp dụng giới hạn một bên thường dùng, ta có : $\mathop {\lim }\limits_{x \to {4^ + }} \frac{1}{{x – 4}} =  + \infty $

b) $\mathop {\lim }\limits_{x \to {2^ + }} \frac{x}{{2 – x}} = \mathop {\lim }\limits_{x \to {2^+ }} \frac{{ – x}}{{x – 2}} = \mathop {\lim }\limits_{x \to {2^ + }} \left( { – x} \right).\mathop {\lim }\limits_{x \to {2^ + }} \frac{1}{{x – 2}}$

Ta có: $\mathop {\lim }\limits_{x \to {2^ + }} \left( { – x} \right) =  – \mathop {\lim }\limits_{x \to {2^ + }} x =  – 2;\mathop {\lim }\limits_{x \to {2^ +}} \frac{1}{{x – 2}} =  +\infty $

$ \Rightarrow \mathop {\lim }\limits_{x \to {2^ – }} \frac{x}{{2 – x}} =  – \infty $

Giải bài 11 trang 86 Toán 11 tập 1

Xét tính liên tục của hàm số

$f(x)=\left\{\begin{matrix}\sqrt{x+4}; x\geq 0\\2cosx; x<0\end{matrix}\right.$

Bài làm

Hàm số $f\left( x \right)$ xác định trên $\mathbb{R}$.

Trên khoảng $\left( {0; + \infty } \right)$, hàm số $f\left( x \right)$ là hàm căn thức xác định trên $\left( {0; + \infty } \right)$ nên hàm số liên tục trên khoảng $\left( {0; + \infty } \right)$.

Trên khoảng $\left( { – \infty ;0} \right)$, hàm số $f\left( x \right)$ là hàm lượng giác xác định trên $\left( { – \infty ;0} \right)$ nên hàm số liên tục trên khoảng $\left( { – \infty ;0} \right)$.

Vậy hàm số $f\left( x \right)$ liên tục trên các khoảng $\left( { – \infty ;0} \right)$ và $\left( {0; + \infty } \right)$.

Ta có: $f\left( 0 \right) = \sqrt {0 + 4}  = 2$

Ta có:       $\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \sqrt {x + 4}  = \sqrt {0 + 4}  = 2$

$\mathop {\lim }\limits_{x \to {0^ – }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ – }} 2\cos x = 2\cos 0 = 2$

Vì $\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ – }} f\left( x \right) = 2$ nên $\mathop {\lim }\limits_{x \to 0} f\left( x \right) = 2 = f\left( 0 \right)$.

Vậy hàm số liên tục tại điểm $x = 0$.

Vậy hàm số liên tục trên $\mathbb{R}$.

Giải bài 12 trang 86 Toán 11 tập 1

Cho hàm số:

$f(x)=\left\{\begin{matrix}\frac{x^{2}-25}{x-5}; x \neq 5\\a; x = 5\end{matrix}\right.$

Tìm a để hàm số y = f(x) liên tục trên $\mathbb{R}$

Bài làm

Trên các khoảng $\left( { – \infty ;5} \right)$ và $\left( {5; + \infty } \right)$, $f\left( x \right) = \frac{{{x^2} – 25}}{{x – 5}}$ là hàm phân thức hữu tỉ nên liên tục trên từng khoảng $\left( { – \infty ;5} \right)$ và $\left( {5; + \infty } \right)$.

Ta có: $f\left( 5 \right) = a$

$\mathop {\lim }\limits_{x \to 5} f\left( x \right) = \mathop {\lim }\limits_{x \to 5} \frac{{{x^2} – 25}}{{x – 5}} = \mathop {\lim }\limits_{x \to 5} \frac{{\left( {x – 5} \right)\left( {x + 5} \right)}}{{x – 5}} = \mathop {\lim }\limits_{x \to 5} \left( {x + 5} \right) = 5 + 5 = 10$

Để hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ thì hàm số $y = f\left( x \right)$ phải liên tục tại điểm ${x_0} = 5$.  Khi đó: $\mathop {\lim }\limits_{x \to 5} f\left( x \right) = f\left( 5 \right) \Leftrightarrow a = 10$.

Vậy với $a = 10$ thì hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$.

Giải bài 13 trang 86 Toán 11 tập 1

Trong một phòng thí nghiệm, nhiệt độ trong tủ sấy được điều khiên tăng từ $10^{o}C$ , mỗi phút tăng $2^{o}C$ trong 60 phút, sau đó giảm mỗi phút $3^{o}C$ trong 40 phút. Hàm số biểu thị nhiệt độ (tính theo $^{o}C$ trong tủ theo thời gian t (tính theo phút) có dạng

$T(t)=\left\{\begin{matrix}10+2t; 0 \leq t\leq 60 \\ k-3t; 60 < t \leq100\end{matrix}\right.$

(k là hằng số)

Biết rằng T(t) liên tục trên tập xác định. Tìm giá trị của k

Bài làm

Hàm số $T\left( t \right)$ có tập xác định là $\left[ {0;100} \right]$.

Ta có: $T\left( {60} \right) = 10 + 2.60 = 130$

$\begin{array}{l}\mathop {\lim }\limits_{t \to {{60}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ + }} \left( {k – 3t} \right) = k – 3.60 = k – 180\\\mathop {\lim }\limits_{t \to {{60}^ – }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ – }} \left( {10 + 2t} \right) = 10 + 2.60 = 130\end{array}$

Để hàm số liên tục trên tập xác định thì hàm số phải liên tục tại điểm ${t_0} = 60$

Khi đó: $\mathop {\lim }\limits_{t \to {{60}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ – }} T\left( t \right) = T\left( {60} \right) \Leftrightarrow k – 180 = 130 \Leftrightarrow k = 310$

Vậy với $k = 310$ thì hàm số $T\left( t \right)$ liên tục trên tập xác định.