Giải toán 11 tập 2 trang 19 bài 2: Phép tính logarit
Giải toán 11 tập 2 trang 19 bài 2: Phép tính logarit
Giải toán 11 tập 2 trang 19 Bài 2 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 11 Chân trời sáng tạo. Mời các em học sinh cùng quý phụ huynh tham khảo.
Giải toán 11 tập 2 trang 14
Hoạt động 1 trang 14 toán 11 tập 2
Độ lớn $M$ (theo độ Richter) của một trận động đất được xác định như Hoạt động mở đầu.
a) Tìm độ lớn theo thang Richter của các trận động đất có biên độ lớn nhất lần lượt là ${10^{3,5}}\mu m;100000\mu m;{100.10^{4,3}}\mu m$.
b) Một trận động đất có biên độ lớn nhất $A = 65000\mu m$ thì độ lớn $M$ của nó phải thoả mãn hệ thức nào?
Lời giải:
a) Với $A = {10^{3,5}}\mu m$ thì $M = 3,5$
Với $A = 100000\mu m = 1{0^5}\mu m$ thì $M = 5$
Với $A = {100.10^{4,3}}\mu m = {10^2}{.10^{4,3}}\mu m = {10^{6,3}}\mu m$ thì $M = 6,3$
a) Với $A = 65000\mu m$ ta có: ${10^M} = 65000$.
Giải toán 11 tập 2 trang 15
Thực hành 1 trang 15 toán 11 tập 2
Tính:
a) ${\log _3}\sqrt[3]{3}$;
b) ${\log _{\frac{1}{2}}}8$;
c) ${\left( {\frac{1}{{25}}} \right)^{{{\log }_5}4}}$.
Lời giải:
a) ${\log _3}\sqrt[3]{3} = {\log _3}{3^{\frac{1}{3}}} = \frac{1}{3}$
b) ${\log _{\frac{1}{2}}}8 = {\log _{\frac{1}{2}}}{2^3} = {\log _{\frac{1}{2}}}{\left( {\frac{1}{2}} \right)^{ – 3}} = – 3$
c) ${\left( {\frac{1}{{25}}} \right)^{{{\log }_5}4}} = {\left( {{5^{ – 2}}} \right)^{{{\log }_5}4}} = {\left( {{5^{{{\log }_5}4}}} \right)^{ – 2}} = {4^{ – 2}} = \frac{1}{{16}}$.
Giải toán 11 tập 2 trang 16
Thực hành 2 trang 16 toán 11 tập 2
Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau (làm tròn kết quả đến chữ số thập phân thứ sáu):
a) ${\log _5}0,5$;
b) $\log 25$;
c) $\ln \frac{3}{2}$.
Hoạt động 2 trang 16 toán 11 tập 2
Cho các số thực dương $a,M,N$ với $a \ne 1$. Bạn Quân đã vẽ sơ đồ và tìm ra công thức biến đổi biểu thức ${\log _a}\left( {MN} \right)$ như sau:
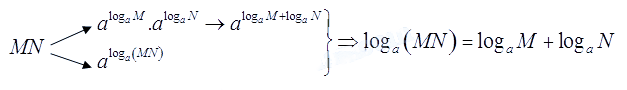
a) Giải thích cách làm của bạn Quân.
b) Vẽ sơ đồ tương tự để tìm công thức biến đổi cho ${\log _a}\frac{M}{N}$ và ${\log _a}{M^\alpha }\left( {\alpha \in \mathbb{R}} \right)$.
Lời giải:
a) Ta có: $M = {a^{{{\log }_a}M}},N = {a^{{{\log }_a}N}} \Rightarrow MN = {a^{{{\log }_a}M}}.{a^{{{\log }_a}N}} = {a^{{{\log }_a}M + {{\log }_a}N}}$
Mặt khác: $MN = {a^{{{\log }_a}\left( {MN} \right)}}$
Vậy ${a^{{{\log }_a}M + {{\log }_a}N}} = {a^{{{\log }_a}\left( {MN} \right)}} \Leftrightarrow {\log _a}M + {\log _a}N = {\log _a}\left( {MN} \right)$
b)

Giải toán 11 tập 2 trang 17
Thực hành 3 trang 17 toán 11 tập 2
Tính:
a) ${\log _5}4 + {\log _5}\frac{1}{4}$;
b) ${\log _2}28 – {\log _2}7$; c) $\log \sqrt {1000} $.
Lời giải:
a) ${\log _5}4 + {\log _5}\frac{1}{4} = {\log _5}\left( {4.\frac{1}{4}} \right) = {\log _5}1 = 0$.
b) ${\log _2}28 – {\log _2}7 = {\log _2}\frac{{28}}{7} = {\log _2}4 = {\log _2}{2^2} = 2$.
c) $\log \sqrt {1000} = \log {1000^{\frac{1}{2}}} = \log {\left( {{{10}^3}} \right)^{\frac{1}{2}}} = \log {10^{\frac{3}{2}}} = \frac{3}{2}$.
Vận dụng trang 17 toán 11 tập 2
Độ lớn $M$ của một trận động đất theo thang Richter được tính theo công thức $M = \log \frac{A}{{{A_0}}}$, trong đó $A$ là biên độ lớn nhất ghi được bởi máy đo địa chấn, ${A_0}$ là biên độ tiêu chuẩn được sử dụng để hiệu chỉnh độ lệch gây ra bởi khoảng cách của máy đo địa chấn so với tâm chấn (ở Hoạt động mở đầu và Hoạt động 1, ${A_0} = 1\mu m$).
a) Tính độ lớn của trận động đất có biên độ $A$ bằng
i) ${10^{5,1}}{A_0}$; ii) $65000{A_0}$.
b) Một trận động đất tại địa điểm $N$ có biên độ lớn nhất gấp ba lần biên độ lớn nhất của trận động đất tại địa điểm $P$. So sánh độ lớn của hai trận động đất.
Lời giải:
a) Với $A = {10^{5,1}}{A_0}$, ta có: $M = \log \frac{A}{{{A_0}}} = \log \frac{{{{10}^{5,1}}{A_0}}}{{{A_0}}} = \log {10^{5,1}} = 5,1$ (Richter).
Với $A = 65000{A_0}$, ta có: $M = \log \frac{A}{{{A_0}}} = \log \frac{{65000{A_0}}}{{{A_0}}} = \log 65000 \approx 4,81$ (Richter).
b) Với ${A_N} = 3{A_P}$, ta có: ${M_N} = \log \frac{{{A_N}}}{{{A_0}}},{M_P} = \log \frac{{{A_P}}}{{{A_0}}}$.
${M_N} – {M_P} = \log \frac{{{A_N}}}{{{A_0}}} – \log \frac{{{A_P}}}{{{A_0}}} = \log \left( {\frac{{{A_N}}}{{{A_0}}}:\frac{{{A_P}}}{{{A_0}}}} \right) = \log \frac{{{A_N}}}{{{A_P}}} = \log \frac{{3{A_N}}}{{{A_P}}} = \log 3 \approx 0,48$
Vậy trận động đất tại địa điểm $N$ lớn hơn trận động đất tại địa điểm $P$ 0,48 Richter.
Giải toán 11 tập 2 trang 18
Hoạt động 3 trang 18 toán 11 tập 2
Khi chưa có máy tính, người ta thường tính các lôgarit dựa trên bảng giá trị các lôgarit thập phân đã được xây dựng sẵn. Chẳng hạn, để tính $x = {\log _2}15$, người ta viết ${2^x} = 15$ rồi lấy lôgarit thập phân hai vế, nhận được $x\log 2 = \log 15$ hay $x = \frac{{\log 15}}{{\log 2}}$.
Sử dụng cách làm này, tính ${\log _a}N$ theo $\log a$ và $\log N$ với $a,N > 0,a \ne 1$.
Lời giải:
Đặt $x = {\log _a}N \Leftrightarrow {a^x} = N \Leftrightarrow \log {a^x} = \log N \Leftrightarrow x\log a = \log N \Leftrightarrow x = \frac{{\log N}}{{\log a}}$
Vậy ${\log _a}N = \frac{{\log N}}{{\log a}}$
Thực hành 4 trang 18 toán 11 tập 2
Tính giá trị các biểu thức sau:
a) ${\log _{\frac{1}{4}}}8$;
b) ${\log _4}5.{\log _5}6.{\log _6}8$.
Lời giải:
a) ${\log _{\frac{1}{4}}}8 = {\log _{{2^{ – 2}}}}{2^3} = \frac{3}{{ – 2}}{\log _2}2 = – \frac{3}{2}$.
b) ${\log _4}5.{\log _5}6.{\log _6}8 = {\log _4}5.\frac{{{{\log }_4}6}}{{{{\log }_4}5}}.\frac{{{{\log }_4}8}}{{{{\log }_4}6}} = {\log _4}8 = {\log _{{2^2}}}{2^3} = \frac{3}{2}{\log _2}2 = \frac{3}{2}$.
Thực hành 5 trang 18 toán 11 tập 2
Đặt ${\log _3}2 = a,{\log _3}7 = b$. Biểu thị ${\log _{12}}21$ theo $a$ và $b$.
Lời giải:
Ta có: ${\log _{12}}21 = \frac{{{{\log }_3}21}}{{{{\log }_3}12}} = \frac{{{{\log }_3}\left( {7.3} \right)}}{{{{\log }_3}\left( {{2^2}.3} \right)}} = \frac{{{{\log }_3}7 + {{\log }_3}3}}{{{{\log }_3}{2^2} + {{\log }_3}3}} = \frac{{{{\log }_3}7 + 1}}{{2{{\log }_3}2 + 1}} = \frac{{b + 1}}{{2a + 1}}$
Giải toán 11 tập 2 trang 19
Giải bài 1 trang 19 Toán 11 tập 2
Tính giá trị các biểu thức sau:
a) $log_{2}16$
b) $log_{3}\frac{1}{27}$
c) log1000
d) $9^{log_{3}12}$
Bài làm
a) $log_{2}16 = log_{2}2^{4} = 4$
b) $log_{3}\frac{1}{27} =log_{3}3^{-3} = -3$
c) $log1000 =log10^{3} = 3$
d) $(3^{log_{3}12})^{2} = 12^{2}=144$
Giải bài 2 trang 19 Toán 11 tập 2
Tìm các giá trị của x để biểu thức sau có nghĩa:
a) $log_{3}(1-2x)$
b) $log_{x+1}5$
Bài làm
a) Để $log_{3}(1-2x)$ có nghĩa thì 1 – 2x > 0 Hay $x < \frac{1}{2}$
b) Để $log_{x+1}5$ có nghĩa thì x + 1 > 0 Hay x > -1
Giải bài 3 trang 19 Toán 11 tập 2
Sử dụng máy tính cầm tay, tính giá trị các biểu thức sau (làm tròn kết quả đến chữ số thập phân thứ tư)
a) $log_{3}15$
b) log8 – log3
c) 3ln2
Bài làm
a) $log_{3}15 = 2,4650$
b) log8 – log3 = 0,4260
c) 3ln2 = 2,0794
Giải bài 4 trang 19 Toán 11 tập 2
Tính giá trị các biểu thức sau:
a) $log_{6}9 + log_{6}4$
b) $log_{5}2 – log_{5}50$
c) $log_{3}\sqrt{5} – \frac{1}{2}log_{3}15$
Bài làm
a) $log_{6}9 + log_{6}4 = log_{6}(9.4)=log_{6}36 = log_{6}6^{2}=2$
b) $log_{5}2 – log_{5}50 = log_{5}\frac{2}{50} = log_{5}\frac{1}{25}=log_{5}5^{-2}=-2$
c) $log_{3}\sqrt{5} – \frac{1}{2}log_{3}15 = log_{3}5^\frac{1}{2}-\frac{1}{2}log_{3}15=\frac{1}{2}log_{3}5-\frac{1}{2}log_{3}15$
$= \frac{1}{2}log_{3}\frac{15}{5}=\frac{1}{2}log_{3}3=\frac{1}{2}$
Giải bài 5 trang 19 Toán 11 tập 2
Tính giá trị các biểu thức sau:
a) $log_{2}9.log_{3}4$
b) $log_{25}\frac{1}{\sqrt{5}}$
c) $log_{2}3.log_{9}\sqrt{5}.log_{5}4$
Bài làm
a) $log_{2}9.log_{3}4=log_{2}3^{2}.log_{3}2^{2}=2.log_{2}3.2.log_{3}2=4.log_{2}3.log_{3}2=4.\frac{log3}{log2}.\frac{log2}{log3}=4$
b) $log_{25}\frac{1}{\sqrt{5}} = log_{25}5^{-\frac{1}{2}}=-\frac{1}{2}log_{25}5 = -\frac{1}{2}log_{25}25^{\frac{1}{2}}=-\frac{1}{2}.\frac{1}{2}.log_{25}25 = \frac{-1}{4}$
c) $log_{2}3.log_{9}\sqrt{5}.log_{5}4=\frac{log_{2}3}{log_{2}2}.\frac{log_{2}\sqrt{5}}{log_{2}9}.\frac{log_{2}4}{log_{2}5}=\frac{log_{2}3}{1}.\frac{log_{2}5^{\frac{1}{2}}}{log_{2}3^{2}}.\frac{log_{2}2^{2}}{log_{2}5}=log_{2}3. \frac{\frac{1}{2}.log_{2}5}{2.log_{2}3}.\frac{2log_{2}2}{log_{2}5}=\frac{1}{2}$
Giải bài 6 trang 19 Toán 11 tập 2
Đặt log2 = a; log3 = b. Biểu thị các biểu thức sau theo a và b
a) log49
b) log612
c) log56
Lời giải
a) ${\log _4}9 = \frac{{\log 9}}{{\log 4}} = \frac{{\log {3^2}}}{{\log {2^2}}} = \frac{{2\log 3}}{{2\log 2}} = \frac{{\log 3}}{{\log 2}} = \frac{b}{a}$.
b) ${\log _6}12 = \frac{{\log 12}}{{\log 6}} = \frac{{\log \left( {{2^2}.3} \right)}}{{\log \left( {2.3} \right)}} = \frac{{\log {2^2} + \log 3}}{{\log 2 + \log 3}} = \frac{{2\log 2 + \log 3}}{{\log 2 + \log 3}} = \frac{{2a + b}}{{a + b}}$.
c) ${\log _5}6 = \frac{{\log 6}}{{\log 5}} = \frac{{\log \left( {2.3} \right)}}{{\log \frac{{10}}{2}}} = \frac{{\log 2 + \log 3}}{{\log 10 – \log 2}} = \frac{{a + b}}{{1 – a}}$.
Giải bài 7 trang 19 Toán 11 tập 2
a) Nước cất có nồng độ H+ là 10−7 mol/L. Tính độ pH của nước cất
b) Một dung dịch có nồng độ H+ gấp 20 lần nồng độ H+ của nước cất. Tính độ pH của dung dịch đó
Lời giải
a) Độ pH của nước cất là: $pH = – \log \left[ {{H^ + }} \right] = – \log \left[ {{{10}^{ – 7}}} \right] = 7$.
b) Nồng độ H+ của dung dịch đó là: ${20.10^{ – 7}}$ mol/L
Độ pH của dung dịch đó là: $pH = – \log \left[ {{H^ + }} \right] = – \log \left[ {{{20.10}^{ – 7}}} \right] \approx 5,7$.
