Giải toán 11 tập 2 trang 25 bài 3: Hàm số mũ. Hàm số logarit
Giải toán 11 tập 2 trang 25 bài 3: Hàm số mũ. Hàm số logarit
Giải toán 11 tập 2 trang 25 Bài 3 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 11 Chân trời sáng tạo. Mời các em học sinh cùng quý phụ huynh tham khảo.
Giải toán 11 tập 2 trang 20
Hoạt động 1 trang 20 toán 11 tập 2
Nguyên phân là quá trình tế bào phân chia thành hai tế bào con giống hệt nhau về mặt di truyền.

Lập bảng sau đây để tính số tế bào được tạo ra từ một tế bào ban đầu sau những lần nguyên phân.
| Số lần nguyên phân | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Số tế bào | 1 | 2 | 4 | ? | ? | ? | ? | ? |
a) Hoàn thành bảng trên vào vở.
b) Gọi $y$ là số tế bào được tạo ra từ một tế bào ban đầu sau $x\left( {x = 0,1,2,…} \right)$ lần nguyên phân. Viết công thức biểu thị $y$ theo $x$.
Lời giải:
a)
| Số lần nguyên phân | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Số tế bào | 1 = 20 | 2 = 21 | 4 = 22 | 8 = 23 | 16 = 24 | 32 = 25 | 64 = 26 | 128 = 27 |
b) Với $x = 0:y = 1 = {2^0}$
Với $x = 1:y = 2 = {2^1}$
Với $x = 2:y = 4 = {2^2}$
Với $x = 3:y = 8 = {2^3}$
…
Với $x = 7:y = 128 = {2^7}$
Vậy $y = {2^x}$.
Hoạt động 2 trang 20 toán 11 tập 2
a) Xét hàm số mũ $y = {2^x}$ với tập xác định $\mathbb{R}$.
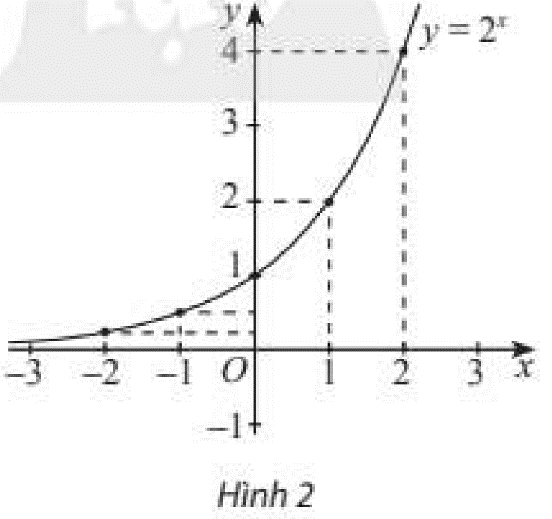
i) Hoàn thành bảng giá trị sau:
ii) Trong mặt phẳng toạ độ $Oxy$, xác định các điểm có toạ độ như bảng trên. Làm tương tự, lấy nhiều điểm $M\left( {x;{2^x}} \right)$ với $x \in \mathbb{R}$ và nối lại ta được đồ thị hàm số $y = {2^x}$ như Hình 2. Từ đồ thị nảy, nêu nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi $x \to + \infty ,x \to – \infty $ và tập giá trị của hàm số đã cho.
b) Lập bảng giá trị và vẽ đồ thị của hàm số $y = {\left( {\frac{1}{2}} \right)^x}$. Từ đó, nêu nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi $x \to + \infty ,x \to – \infty $ và tập giá trị của hàm số này.
Lời giải:
a) i)
| x | -2 | -1 | 0 | 1 | 2 |
| y | 14 | 12 | 1 | 2 | 4 |
ii) ‒ Hàm số liên tục trên $\mathbb{R}$.
‒ Hàm số đồng biến trên $\mathbb{R}$.
‒ Giới hạn: $\mathop {\lim }\limits_{x \to + \infty } {2^x} = + \infty ;\mathop {\lim }\limits_{x \to – \infty } {2^x} = 0$.
‒ Tập giá trị: $\left( {0; + \infty } \right)$.
b) Bảng giá trị:
Đồ thị hàm số $y = {\left( {\frac{1}{2}} \right)^x}$:

‒ Hàm số liên tục trên $\mathbb{R}$.
‒ Hàm số nghịch biến trên $\mathbb{R}$.
‒ Giới hạn: $\mathop {\lim }\limits_{x \to + \infty } {\left( {\frac{1}{2}} \right)^x} = 0;\mathop {\lim }\limits_{x \to – \infty } {\left( {\frac{1}{2}} \right)^x} = + \infty $.
‒ Tập giá trị: $\left( {0; + \infty } \right)$.
Giải toán 11 tập 2 trang 22
Thực hành 1 trang 22 toán 11 tập 2
Trên cùng một hệ trục toạ độ, vẽ đồ thị các hàm số $y = {3^x}$ và $y = {\left( {\frac{1}{3}} \right)^x}$.
Lời giải:
Bảng giá trị:
‒ Hàm số $y = {3^x}$:
| x | −2 | −1 | 0 | 1 | 2 |
| y | 19 | 13 | 1 | 3 | 9 |
‒ Hàm số $y = {\left( {\frac{1}{3}} \right)^x}$:

‒ Đồ thị:
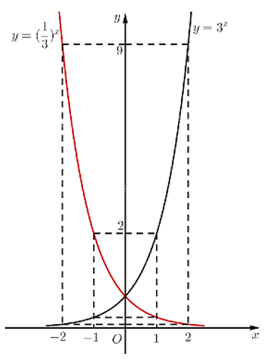
Thực hành 2 trang 22 toán 11 tập 2
So sánh các cặp số sau:
a) $0,{85^{0,1}}$ và $0,{85^{ – 0,1}}$.
b) ${\pi ^{ – 1,4}}$ và ${\pi ^{ – 0,5}}$.
c) $\sqrt[4]{3}$ và $\frac{1}{{\sqrt[4]{3}}}$.
Lời giải:
a) Do $0,85 < 1$ nên hàm số $y = 0,{85^x}$ nghịch biến trên $\mathbb{R}$.
Mà $0,1 > – 0,1$ nên $0,{85^{0,1}} < 0,{85^{ – 0,1}}$.
b) Do $\pi > 1$ nên hàm số $y = {\pi ^x}$ đồng biến trên $\mathbb{R}$.
Mà $ – 1,4 < – 0,5$ nên ${\pi ^{ – 1,4}} < {\pi ^{ – 0,5}}$.
c) $\sqrt[4]{3} = {3^{\frac{1}{4}}};\frac{1}{{\sqrt[4]{3}}} = \frac{1}{{{3^{\frac{1}{4}}}}} = {3^{ – \frac{1}{4}}}$.
Do $3 > 1$ nên hàm số $y = {3^x}$ đồng biến trên $\mathbb{R}$.
Mà $\frac{1}{4} > – \frac{1}{4}$ nên ${3^{\frac{1}{4}}} > {3^{ – \frac{1}{4}}} \Leftrightarrow \sqrt[4]{3} > \frac{1}{{\sqrt[4]{3}}}$.
Vận dụng 1 trang 22 toán 11 tập 2
Khối lượng vi khuẩn của một mẻ nuôi cấy sau $t$ giờ kể từ thời điểm ban đầu được cho bởi công thức $M\left( t \right) = 50.1,{06^t}\left( g \right)$.
(Nguồn: Sinh học 10, NXB Giáo dục Việt Nam, năm 2017, trang 101)
a) Tìm khối lượng vi khuẩn tại thời điểm bắt đầu nuôi cấy (gọi là khối lượng ban đầu).
b) Tính khối lượng vi khuẩn sau 2 giờ và sau 10 giờ (làm tròn kết quả đến hàng phần trăm).
c) Khối lượng vi khuẩn tăng dần hay giảm dần theo thời gian? Tại sao?
Lời giải:
a) Khối lượng vi khuẩn tại thời điểm bắt đầu nuôi cấy là:
$M\left( 0 \right) = 50.1,{06^0} = 50\left( g \right)$
b) Khối lượng vi khuẩn sau 2 giờ là:
$M\left( 2 \right) = 50.1,{06^2} = 56,18\left( g \right)$
Khối lượng vi khuẩn sau 10 giờ là:
$M\left( {10} \right) = 50.1,{06^{10}} \approx 89,54\left( g \right)$
c) Xét hàm số $M\left( t \right) = 50.1,{06^t}$.
Vì $1,06 > 1$ nên hàm số $M\left( t \right) = 50.1,{06^t}$ là hàm số đồng biến. Vậy khối lượng vi khuẩn tăng dần theo thời gian.
Hoạt động 3 trang 22 toán 11 tập 2
Cho $s$ và $t$ là hai đại lượng liên hệ với nhau theo công thức $s = {2^t}$.
a) Với mỗi giá trị của $t$ nhận giá trị trong $\mathbb{R}$, tìm được bao nhiêu giá trị tương ứng của $s$? Tại sao?
b) Với mỗi giá trị của $s$ thuộc $\left( {0; + \infty } \right)$, có bao nhiêu giá trị tương ứng của $t$?
c) Viết công thức biểu thị $t$ theo $s$ và hoàn thành bảng sau.

Lời giải:
a) Với mỗi giá trị của $t$ thuộc $\mathbb{R}$, tìm được duy nhất một giá trị tương ứng của $s$.
b) Với mỗi giá trị của $s$ thuộc $\left( {0; + \infty } \right)$, có duy nhất một giá trị tương ứng của $t$.
c) $s = {2^t} \Leftrightarrow t = {\log _2}s$
Ta có:

Giải toán 11 tập 2 trang 23
Hoạt động 4 trang 23 toán 11 tập 2
a) Xét hàm số $y = {\log _2}x$ với tập xác định $D = \left( {0; + \infty } \right)$.

i) Hoàn thành bảng giá trị sau:
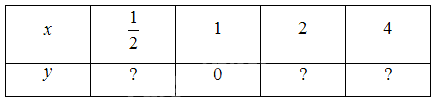
ii) Trong mặt phẳng toạ độ $Oxy$, xác định các điểm có toạ độ như bảng trên. Làm tương tự, lấy nhiều điểm $M\left( {x;{{\log }_2}x} \right)$ với $x > 0$ và nối lại ta được đồ thị hàm số $y = {\log _2}x$ như Hình 4. Từ đồ thị này, nêu nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi $x \to + \infty ,x \to {0^ + }$ và tập giá trị của hàm số đã cho.
b) Lập bảng giá trị và vẽ đồ thị của hàm số $y = {\log _{\frac{1}{2}}}x$. Từ đó, nhận xét về tính liên tục, tính đồng biến, nghịch biến, giới hạn khi $x \to + \infty ,x \to {0^ + }$ và tập giá trị của hàm số này.
Lời giải:
a) i)

ii) ‒ Hàm số liên tục trên $\left( {0; + \infty } \right)$.
‒ Hàm số đồng biến trên $\left( {0; + \infty } \right)$.
‒ Giới hạn: $\mathop {\lim }\limits_{x \to + \infty } {\log _2}x = + \infty ;\mathop {\lim }\limits_{x \to {0^ + }} {\log _2}x = – \infty $.
‒ Tập giá trị: $\mathbb{R}$.
b) Bảng giá trị:

Đồ thị hàm số $y = {\log _{\frac{1}{2}}}x$:
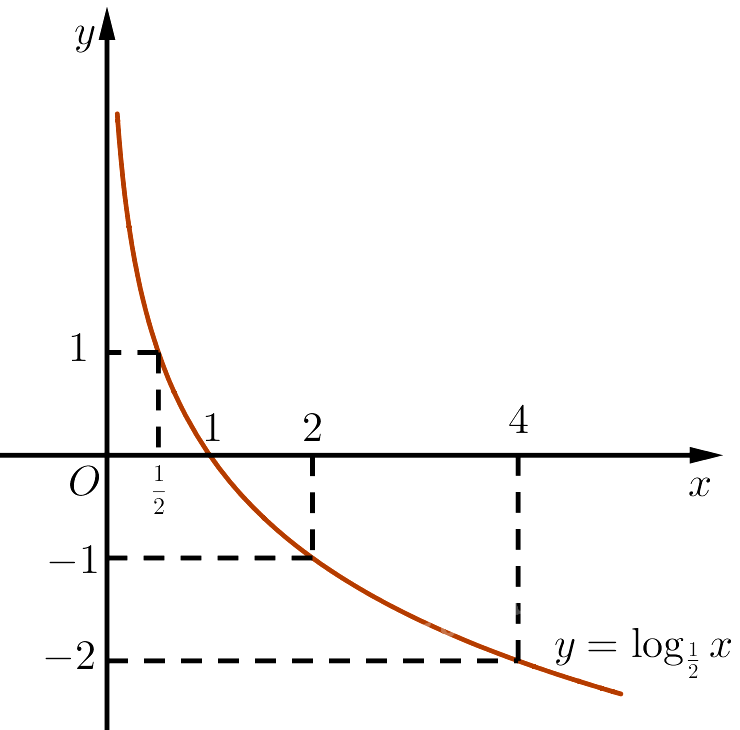
‒ Hàm số liên tục trên $\left( {0; + \infty } \right)$.
‒ Hàm số nghịch biến trên $\left( {0; + \infty } \right)$.
‒ Giới hạn: $\mathop {\lim }\limits_{x \to + \infty } {\log _{\frac{1}{2}}}x = – \infty ;\mathop {\lim }\limits_{x \to {0^ + }} {\log _{\frac{1}{2}}}x = + \infty $.
‒ Tập giá trị: $\mathbb{R}$.
Giải toán 11 tập 2 trang 24
Thực hành 3 trang 24 toán 11 tập 2
Trên cùng một hệ trục toạ độ, vẽ đồ thị các hàm số $y = {\log _3}x$ và $y = {\log _{\frac{1}{3}}}x$.
Lời giải:
Bảng giá trị:
‒ Hàm số $y = {\log _3}x$:

‒ Hàm số $y = {\log _{\frac{1}{3}}}x$:
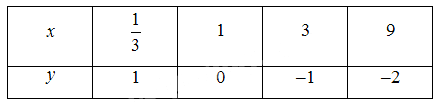
‒ Đồ thị:

Thực hành 4 trang 24 toán 11 tập 2
So sánh các cặp số sau:
a) ${\log _{\frac{1}{2}}}4,8$ và ${\log _{\frac{1}{2}}}5,2$;
b) ${\log _{\sqrt 5 }}2$ và ${\log _5}2\sqrt 2 $;
c) $ – {\log _{\frac{1}{4}}}2$ và ${\log _{\frac{1}{2}}}0,4$.
Lời giải:
a) Hàm số $y = {\log _{\frac{1}{2}}}x$ có cơ số $\frac{1}{2} < 1$ nên nghịch biến trên $\left( {0; + \infty } \right)$.
Mà $4,8 < 5,2$ nên ${\log _{\frac{1}{2}}}4,8 > {\log _{\frac{1}{2}}}5,2$.
b) ${\log _{\sqrt 5 }}2 = {\log _{{5^{\frac{1}{2}}}}}2 = 2{\log _5}2 = {\log _5}{2^2} = {\log _5}4$
Hàm số $y = {\log _5}x$ có cơ số $5 > 1$ nên đồng biến trên $\left( {0; + \infty } \right)$.
Mà $4 > 2\sqrt 2 $ nên ${\log _5}4 > {\log _5}2\sqrt 2 $. Vậy ${\log _{\sqrt 5 }}2 > {\log _5}2\sqrt 2 $
c) $ – {\log _{\frac{1}{4}}}2 = – {\log _{{{\left( {\frac{1}{2}} \right)}^2}}}2 = – \frac{1}{2}{\log _{\frac{1}{2}}}2 = {\log _{\frac{1}{2}}}{2^{ – \frac{1}{2}}} = {\log _{\frac{1}{2}}}\frac{1}{{\sqrt 2 }}$
Hàm số $y = {\log _{\frac{1}{2}}}x$ có cơ số $\frac{1}{2} < 1$ nên nghịch biến trên $\left( {0; + \infty } \right)$.
Mà $\frac{1}{{\sqrt 2 }} > 0,4$ nên ${\log _{\frac{1}{2}}}\frac{1}{{\sqrt 2 }} < {\log _{\frac{1}{2}}}0,4$. Vậy $ – {\log _{\frac{1}{4}}}2 < {\log _{\frac{1}{2}}}0,4$
Giải toán 11 tập 2 trang 25
Vận dụng 2 trang 25 toán 11 tập 2
Mức cường độ âm được tính theo công thức như ở Ví dụ 6.
a) Tiếng thì thầm có cường độ âm $I = {10^{ – 10}}W/{m^2}$ thì có mức cường độ âm bằng bao nhiêu?
b) Để nghe trong thời gian dài mà không gây hại cho tai, âm thanh phải có cường độ không vượt quá 100 000 lần cường độ của tiếng thì thẩm. Âm thanh không gây hại cho tai khi nghe trong thời gian dài phải ở mức cường độ âm như thế nào?
Lời giải:
a) Mức cường độ âm của tiếng thì thầm là:
$L = 10\log \left( {\frac{I}{{{I_0}}}} \right) = 10\log \left( {\frac{{{{10}^{ – 10}}}}{{{{10}^{ – 12}}}}} \right) = 20\left( {dB} \right)$
b) Để âm thanh không gây hại cho tai, âm thanh phải có cường độ âm không vượt quá:
$I = {100000.10^{ – 10}} = 1{0^{ – 5}}W/{m^2}$
Âm thanh không gây hại cho tai nghe trong thời gian dài phải ở mức cường độ âm không vượt quá:
$L = 10\log \left( {\frac{I}{{{I_0}}}} \right) = 10\log \left( {\frac{{{{10}^{ – 5}}}}{{{{10}^{ – 12}}}}} \right) = 70\left( {dB} \right)$
Giải bài 1 trang 25 Toán 11 tập 2
Vẽ đồ thị các hàm số sau:
a) $y=4^{x}$
b) $y = (\frac{1}{4})^{x}$
Bài làm
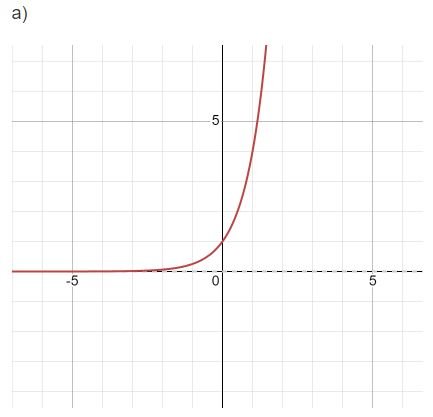
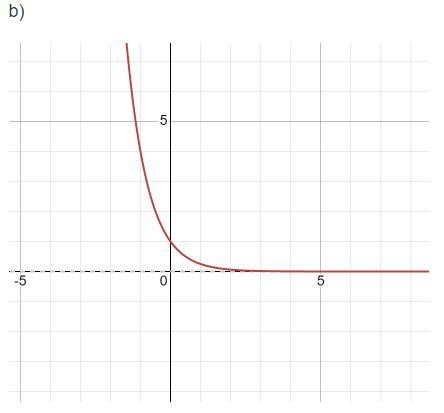
Giải bài 2 trang 25 Toán 11 tập 2
So sánh các cặp số sau
a) 1,30,7 và 1,30,6
b) 0,75−2,3 và 0,75−2,4
Bài làm
a) Vì 1,3 > 1 nên hàm số y = 1,3x là hàm số đồng biến trên R
Mà 0,7 > 0, 6 nên 1,30,7 > 1,30,6
b) Vì 0,75 < 1 nên hàm số y = 0,75x là hàm số nghịch biến trên R
Mà -2,3 > -2,4 nên 0,75−2,3 > 0,75−2,4
Giải bài 3 trang 25 Toán 11 tập 2
Tìm tập xác định của các hàm số:
a) log2(3 − 2x)
b) log3(x2 + 4x)
Bài làm
a) $log_{2}(3-2x)$ xác định khi 3 – 2x > 0 Hay x < $\frac{3}{2}$
b) $log_{3}(x^{2}+4x)$ xác định khi $x^{2}+4x$ > 0 hay x > 0 hoặc x < -4
Giải bài 4 trang 25 Toán 11 tập 2
Vẽ đồ thị các hàm số
a) y = logx
b) $y=log_{\frac{1}{4}}x$
Bài làm
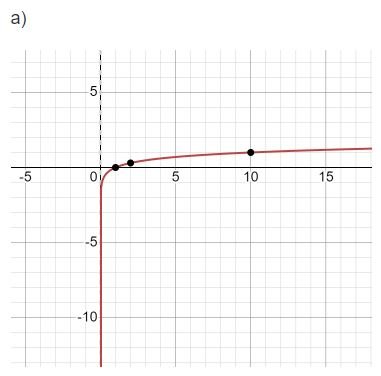
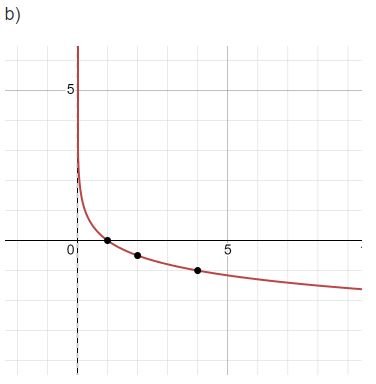
Giải bài 5 trang 25 Toán 11 tập 2
So sánh các cặp số sau:
a) $log_{\pi}0,8 và log_{\pi}1,2$
b) $log_{0,3}2 và log_{0,3}2,1$
Bài làm
a) Vì $\pi > 1$ nên hàm số $log_{\pi}x$ đồng biến trên $(0;+\infty)$
Mà 0,8 < 1,2 nên $log_{\pi}0,8 < log_{\pi}1,2$
b) Vì 0,3 > 1 nên hàm số $log_{0,3}x$ nghịch biến trên $(0;+\infty)$
Mà 2 < 2,1 nên $log_{0,3}2>log_{0,3}2,1$
Giải bài 6 trang 25 Toán 11 tập 2
Cường độ ánh sáng I dưới mặt biển giảm dần theo độ sâu theo công thức I = I0.ad, trong đó I0 là cường độ ánh sáng tại mặt nước biển, a là hằng số (a > 0) và d là độ sâu tính bằng mét tính từ mặt nước biển.
a) Có thể khẳng định rằng 0 < a < 1 không? Giải thích.
b) Biết rằng cường độ ánh sáng tại độ sâu 1 m bằng 0,95I0. Tìm giá trị của a
c) Tại độ sâu 20m, cường độ ánh sáng bằng bao nhiêu phần trăm so với I0? (Làm tròn kết quả đến hàng đơn vị)
Bài làm
a) Vì cường độ ánh sáng giảm dần theo độ sâu nên hàm số $I = {I_0}.{a^d}$ nghịch biến.
Vậy $0 < a < 1$.
b) Ta có: $I = {I_0}.{a^d} \Leftrightarrow 0,95{I_0} = {I_0}.{a^1} \Leftrightarrow a = 0,95$.
c) Ta có: $I = {I_0}.{a^d} = {I_0}.0,{95^{20}} \approx 0,36{I_0}$.
Vậy tại độ sâu 20 m, cường độ ánh sáng bằng 36% phần trăm so với ${I_0}$
Giải bài 7 trang 25 Toán 11 tập 2
Công thức $h = -19,4log\frac{P}{P_{0}}$ là mô hình đơn giản cho phép tính độ cao h so với mặt nước biển của một vị trí trong không trung (tính bằng kilômét) theo áp suất không khí P tại điểm đó và áp suất $P_{0}$ của không khí tại mặt nước biển (cùng tính bằng $P_{a}$ – đơn vị áp suất, đọc là Pascal)
a) Nếu áp suất không khí ngoài máy bay bằng $\frac{1}{2}P_{0}$ thì máy bay đang ở độ cao nào?
b) Áp suất không khí tại đỉnh của ngọn núi A bằng $\frac{4}{5}$ lần áp suất không khí tại đỉnh của ngọn núi B. Ngọn núi nào cao hơn và cao hơn bao nhiêu kilômét? (Làm tròn kết quả đến hàng phần mười)
Lời giải
a) Độ cao của máy bay khi áp suất không khí ngoài máy bay bằng $\frac{1}{2}{P_0}$ là:
$h = – 19,4.\log \frac{{\frac{1}{2}{P_0}}}{{{P_0}}} = – 19,4.\log \frac{1}{2} \approx 5,84\left( {km} \right)$
b) Độ cao của ngọn núi A là: ${h_A} = – 19,4.\log \frac{{{P_A}}}{{{P_0}}}$
Độ cao của ngọn núi B là: ${h_B} = – 19,4.\log \frac{{{P_B}}}{{{P_0}}}$
Áp suất không khí tại đỉnh của ngọn núi A bằng $\frac{4}{5}$ lần áp suất không khí tại đỉnh của ngọn núi B nên ta có: ${P_A} = \frac{4}{5}{P_B} \Leftrightarrow \frac{{{P_A}}}{{{P_B}}} = \frac{4}{5}$
Ta có:
$\begin{array}{l}{h_A} – {h_B} = \left( { – 19,4.\log \frac{{{P_A}}}{{{P_0}}}} \right) – \left( { – 19,4.\log \frac{{{P_B}}}{{{P_0}}}} \right) = – 19,4.\log \frac{{{P_A}}}{{{P_0}}} + 19,4.\log \frac{{{P_B}}}{{{P_0}}}\\ = – 19,4\log \left( {\frac{{{P_A}}}{{{P_0}}}:\frac{{{P_B}}}{{{P_0}}}} \right) = – 19,4\log \frac{{{P_A}}}{{{P_B}}} = – 19,4\log \frac{4}{5} \approx 1,88\left( {km} \right)\end{array}$
Vậy ngọn núi A cao hơn ngọn núi B 1,88 km.
