Giải toán 11 tập 2 trang 93 bài 1: Biến cố giao và quy tắc nhân xác suất

Giải toán 11 tập 2 trang 93 Bài 1 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 11 Chân trời sáng tạo. Mời các em học sinh cùng quý phụ huynh tham khảo.

Giải toán 11 tập 2 trang 89

Hoạt động 1 trang 89 toán 11 tập 2

Gieo hai con xúc xắc cân đối và đồng chất. Gọi $A$ là biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 5”, $B$ là biến cố “Tích số chấm xuất hiện trên hai con xúc xắc bằng 6”.

a) Hãy viết tập hợp mô tả các biến cố trên.

b) Hãy liệt kê các kết quả của phép thử làm cho cả hai biến cố $A$ và $B$ cùng xảy ra.

Lời giải:

a) $A = \left\{ {\left( {1;4} \right);\left( {2;3} \right);\left( {3;2} \right);\left( {4;1} \right)} \right\}$

$B = \left\{ {\left( {1;6} \right);\left( {2;3} \right);\left( {3;2} \right);\left( {6;1} \right)} \right\}$

b) Các kết quả của phép thử làm cho cả hai biến cố $A$ và $B$ cùng xảy ra là $\left( {2;3} \right);\left( {3;2} \right)$

Thực hành 1 trang 89 toán 11 tập 2

Tiếp tục với phép thử ở Ví dụ 1.

a) Gọi $D$ là biến cố “Số chấm xuất hiện trên con xúc xắc thứ nhất là 3”. Hãy xác định các biến cố $AD,BD$ và $C{\rm{D}}$.

b) Gọi $\bar A$ là biến cố đối của biến cố $A$. Hãy viết tập hợp mô tả các biến cố giao $\bar AB$ và $\bar AC$.

Lời giải:

a) $D = \left\{ {\left( {3;1} \right);\left( {3;2} \right);\left( {3;3} \right);\left( {3;4} \right);\left( {3;5} \right);\left( {3;6} \right)} \right\}$

$A{\rm{D}} = \left\{ {\left( {3;2} \right)} \right\};B{\rm{D}} = \left\{ {\left( {3;2} \right)} \right\};C{\rm{D}} = \left\{ {\left( {3;1} \right)} \right\}$

b) $\bar AB = \left\{ {\left( {1;6} \right);\left( {6;1} \right)} \right\}$

$\bar A{\rm{C}} = \left\{ {\left( {1;6} \right);\left( {6;1} \right);\left( {1;5} \right);\left( {5;1} \right);\left( {1;3} \right);\left( {3;1} \right);\left( {1;2} \right);\left( {2;1} \right);\left( {1;1} \right)} \right\}$

Hoạt động 2 trang 89 toán 11 tập 2

 Gieo hai con xúc xắc cân đối và đồng chất. Gọi $A$ là biến cố “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 5”, gọi $B$ là biến cố “Xuất hiện hai mặt có củng số chấm”. Hai biến cố $A$ và $B$ có thể đồng thời cùng xảy ra không?

Lời giải:

$A = \left\{ {\left( {1;4} \right);\left( {2;3} \right);\left( {3;2} \right);\left( {4;1} \right)} \right\}$

$B = \left\{ {\left( {1;1} \right);\left( {2;2} \right);\left( {3;3} \right);\left( {4;4} \right);\left( {5;5} \right);\left( {6;6} \right)} \right\}$

Hai biến cố $A$ và $B$ không thể đồng thời cùng xảy ra.

Giải toán 11 tập 2 trang 90

Thực hành 2 trang 90 toán 11 tập 2

Hãy tìm một biến cố khác rỗng và xung khắc với cả ba biến cố $A,B$ và $C$ trong Ví dụ 1.

Lời giải:

$D = \left\{ {\left( {2;6} \right);\left( {3;5} \right);\left( {4;4} \right);\left( {5;3} \right);\left( {6;2} \right)} \right\}$: “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 8”.

Thực hành 3 trang 90 toán 11 tập 2

a) Hai biến cố đối nhau có xung khắc với nhau không?

b) Hai biến cố xung khắc có phải là hai biến cố đối nhau không?

Lời giải:

a) Hai biến cố đối không đồng thời xảy ra nên hai biến cố đối nhau xung khắc với nhau.

b) Hợp của hai biến cố xung khắc có thể không bằng không gian mẫu nên hai biến cố xung khắc không phải là hai biến cố đối nhau.

Hoạt động 3 trang 90 toán 11 tập 2

An và Bình mỗi người gieo một con xúc xắc cân đối và đồng chất. Gọi $A$ là biến cố “An gieo được mặt 6 chấm” và $B$ là biến cố “Bình gieo được mặt 6 chấm”.

a) Tính xác suất của biến cố $B$.

b) Tính xác suất của biến cố $B$ trong hai trường hợp sau:

• Biến cố $A$ xảy ra

• Biến có $A$ không xảy ra.

Lời giải:

a) $n\left( \Omega  \right) = 6;B = \left\{ 6 \right\} \Rightarrow n\left( B \right) = 1 \Rightarrow P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega  \right)}} = \frac{1}{6}$.

b) • Biến cố $A$ xảy ra: $P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega  \right)}} = \frac{1}{6}$.

• Biến có $A$ không xảy ra: $P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega  \right)}} = \frac{1}{6}$.

Giải toán 11 tập 2 trang 91

Thực hành 4 trang 91 toán 11 tập 2

Hãy chỉ ra 2 biến cố độc lập trong phép thử tung 2 đồng xu cân đối và đồng chất.

Lời giải:

Hai biến cố độc lập là:

Biến cố $A$: “Đồng xu thứ nhất xuất hiện mặt sấp”

Biến cố $B$: “Đồng xu thứ hai xuất hiện mặt ngửa”

Hoạt động 4 trang 91 toán 11 tập 2

Trong Hoạt động 3, hãy tính và so sánh $P\left( {AB} \right)$ với $P\left( A \right)P\left( B \right)$.

Lời giải:

$AB = \left\{ {\left( {6;6} \right)} \right\},n\left( {AB} \right) = 1,n\left( \Omega\right) = 36 \Rightarrow P\left( {AB} \right) = \frac{{n\left( {AB} \right)}}{{n\left( \Omega \right)}} = \frac{1}{{36}}$

$P\left( A \right) = \frac{1}{6},P\left( B \right) = \frac{1}{6} \Rightarrow P\left( A \right)P\left( B \right) = \frac{1}{{36}}$

Vậy $P\left( {AB} \right) = P\left( A \right)P\left( B \right)$.

Giải toán 11 tập 2 trang 92

Thực hành 5 trang 92 toán 11 tập 2

Hãy trả lời câu hỏi ở nếu Nguyệt và Nhi bắn độc lập với nhau.

Lời giải:

Vì hai biến cố “Nguyệt bắn trúng tâm bia” và “Nhi bắn trúng tâm bia” là hai biến cố độc lập nên xác suất để cả hai bạn cùng bắn trúng tâm bia là: $P = 0,9.0,8 = 0,72$.

Giải toán 11 tập 2 trang 93

Giải bài 1 trang 93 Toán 11 tập 2

Hộp thứ nhất chứ 3 tấm thẻ cùng loại được đánh số lần lượt từ 1 đến 3. Hộp thứ hai chứa 5 tấm thẻ cùng loại được đánh số từ 1 đến 5. Lấy ngẫu nhiên từ mỗi hộp 1 thẻ. Gọi A là biến cố “Tổng các số ghi trên 2 thẻ bằng 6”, B là biến cố “Tích các số ghi trên 2 thẻ là số lẻ”

a) Hãy viết tập hợp mô tả biến cố AB và tính P(AB)

b) Hãy tìm một biến cố khác rổng và xung khắc với cả hai biến cố A và B

Bài làm

a) AB = {(1;5);(3;3)}

P(AB) = P(A).P(B) = $\frac{3}{15} . \frac{6}{15}$ = 0,08

b) C là biến cố “Tích các số ghi trên 2 thẻ bằng 6”

Giải bài 2 trang 93 Toán 11 tập 2

Một hộp chứa 21 tấm thẻ cùng loại được đánh số từ 1 đến 21. Chọn ngẫu nhiên 1 thẻ từ hộp. Gọi A là biến cố “Số ghi trên thẻ được chọn chia hết cho 2”, B là biến cố “Số ghi trên thẻ được chọn chia hết cho 3”

a) Hãy mô tả bằng lời biến cố AB

b) Hai biến cố A và B có độc lập không? Tại sao

Bài làm

a) AB là biến cố “Số ghi trên thẻ được chọn chia hết cho 6”

b) Hai biến cố A và B độc lập. Do nếu biến cố A xảy ra hay không thì xác suất xảy ra biến cố B không đổi

Giải bài 3 trang 93 Toán 11 tập 2

Cho A và B là hai biến cố độc lập

a) Biết P(A) = 0,7 và P(B) = 0,2. Hãy tính xác suất của các biến cố AB, $\bar{A} B$ và $A\bar{B}$

b) Biết P(A) = 0,5 và P(AB) = 0,3. Hãy tính xác suất của các biến cố aB, $\bar{A} B$ và $A\bar{B}$

Bài làm

a) $P\left( {\bar A} \right) = 1 – P\left( A \right) = 1 – 0,7 = 0,3;P\left( {\bar B} \right) = 1 – P\left( B \right) = 1 – 0,2 = 0,8$

$\begin{array}{l}P\left( {AB} \right) = P\left( A \right)P\left( B \right) = 0,7.0,2 = 0,14\\P\left( {\bar AB} \right) = P\left( {\bar A} \right)P\left( B \right) = 0,3.0,2 = 0,06\\P\left( {\bar A\bar B} \right) = P\left( {\bar A} \right)P\left( {\bar B} \right) = 0,3.0,8 = 0,24\end{array}$

b) $P\left( {\bar A} \right) = 1 – P\left( A \right) = 1 – 0,5 = 0,5$

$\begin{array}{l}P\left( B \right) = \frac{{P\left( {AB} \right)}}{{P\left( A \right)}} = \frac{{0,3}}{{0,5}} = 0,6 \Rightarrow P\left( {\bar B} \right) = 1 – P\left( B \right) = 1 – 0,6 = 0,4\\P\left( {\bar AB} \right) = P\left( {\bar A} \right)P\left( B \right) = 0,5.0,6 = 0,3\\P\left( {\bar A\bar B} \right) = P\left( {\bar A} \right)P\left( {\bar B} \right) = 0,5.0,4 = 0,2\end{array}$

Giải bài 4 trang 93 Toán 11 tập 2

Một xạ thủ bắn lần lượt 2 viên đạn vào một bia. Xác suất trúng đích của viên thứ nhất và thứ hai lần lượt là 0,9 và 0,6. Biết rằng kết quả các lần bắn là độc lập nhau. Tính xác suất của các biến cố sau bằng cách sử dụng sơ đồ hình cây

a) “Cả 2 lần bắn đều trúng đích”

b) “Cả 2 lần bắn đều không trúng đích”

c) “Lần bắn thứ nhất trúng đích, lần bắn thứ hai không trúng đích”

Lời giải

Do hai lần bắn độc lập nên ta có sơ đồ hình cây như sau:

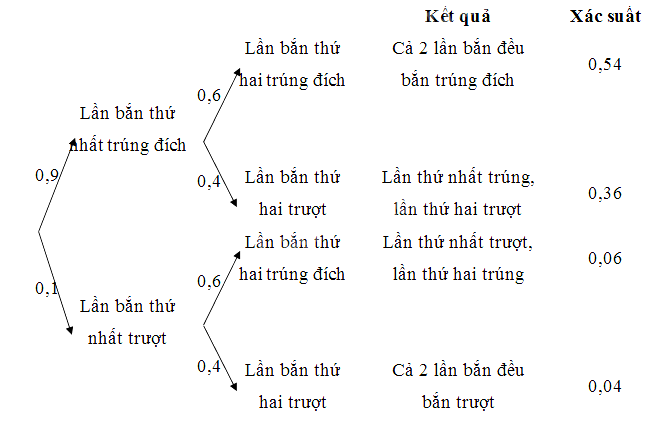
Theo sơ đồ trên thì:

a) Xác suất cả 2 lần bắn đều trúng đích là 0,54.

b) Xác suất cả 2 lần bắn đều không trúng đích là 0,04.

c) Xác suất lần bắn thứ nhất trúng đích, lần bắn thứ hai không trúng đích là 0,36.

Giải bài 5 trang 93 Toán 11 tập 2

Một bệnh truyền nhiễm có xác suất truyền bệnh là 0,8 nếu tiếp xúc với người bệnh mà không đeo khẩu trang; là 0,1 nếu tiếp xúc với người đó mà đeo khẩu trang. Anh Lâm tiếp xúc với 1 người bệnh hai lần, trong đó có một lần đeo khẩu trang và một lần không đeo khẩu trang. Tính xác suất anh Lâm bị lây bệnh từ người bệnh mà anh tiếp xúc đó.

Lời giải

Gọi A là biến cố anh Lâm không bị lây bệnh khi tiếp xúc với người bênh đeo khẩu trang. P(A) = 0,9.

Gọi B là biến cố anh Lâm không bị lây bệnh khi tiếp xúc với người bênh không đeo khẩu trang. P(B) = 1 – 0,8 = 0,2.

Xác suất anh Lâm không bị lây bệnh là: P(A).P(B) = 0,9.0,2 = 0,18.

Xác suất anh Lâm bị lây bệnh là: 1 – 0,18 = 0,82.