Toán 11 tập 2 trang 19 Bài 20: Hàm số mũ và hàm số lôgarit

Giải toán 11 tập 2 trang 19 Bài 20 sách Kết nối tri thức có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 11 Kết nối tri thức. Mời các em học sinh cùng quý phụ huynh tham khảo.

Toán 11 tập 2 trang 16

Mở đầu trang 16 Toán 11 Tập 2:

Sự tăng trưởng dân số được ước tính theo công thức tăng trưởng mũ sau:

A = Pe^rt,

trong đó P là dân số của năm lấy làm mốc, A là dân số sau t năm, r là tỉ lệ tăng dân số hằng năm. Biết rằng vào năm 2020, dân số Việt Nam khoảng 97,34 triệu người và tỉ lệ tăng dân số là 0,91% (theo danso.org). Nếu tỉ lệ tăng dân số này giữ nguyên, hãy ước tính dân số Việt Nam vào năm 2050.

Lời giải:

Sau bài học, ta giải quyết được bài toán như sau:

Theo bài ra ta có P = 97,34; r = 0,91%.

Từ năm 2020 đến năm 2050 là 30 năm nên t = 30.

Ước tính dân số Việt Nam vào năm 2050 là

A = Pe^rt = 97,34 ∙ e^{0,91% ∙ 30} ≈ 127,9 (triệu người).

HĐ1 trang 16 Toán 11 Tập 2:

Nhận biết hàm số mũ

a) Tính y = 2^x khi x lần lượt nhận các giá trị – 1; 0; 1. Với mỗi giá trị của x có bao nhiêu giá trị của y = 2^x tương ứng?

b) Với những giá trị nào của x, biểu thức y = 2^x có nghĩa?

Lời giải:

a) Ta có:

+ Với x = – 1 thì y = 2^{– 1} = $\frac{1}{2}$

+ Với x = 0 thì y = 2⁰ = 1.

+ Với x = 1 thì y = 2¹ = 2.

Ta nhận thấy với mỗi giá trị của x có duy nhất một giá trị của y = 2^x tương ứng.

b) Biểu thức y = 2^x có nghĩa với mọi giá trị của x.

Câu hỏi trang 16 Toán 11 Tập 2

Trong các hàm số sau, những hàm số nào là hàm số mũ? Khi đó hãy chỉ ra cơ số.

a) $\displaystyle y={{\left( {\sqrt{2}} \right)}^{x}}$

b) y = 2^{– x};

c) $\displaystyle y={{8}^{{\frac{x}{3}}}}$

d) y = x^{– 2}.

Lời giải:

a) Hàm số $\displaystyle y={{\left( {\sqrt{2}} \right)}^{x}}$ là hàm số mũ với cơ số $\displaystyle \sqrt{2}$

b) Ta có y = 2^{– x} = (2^{– 1})^x = $\displaystyle {{\left( {\frac{1}{2}} \right)}^{x}}$ Do đó, hàm số đã cho là hàm số mũ với cơ số $\displaystyle \frac{1}{2}$

c) Ta có $\displaystyle y={{8}^{{\frac{x}{3}}}}={{\left( {\sqrt[3]{8}} \right)}^{x}}={{2}^{x}}$ Do đó, hàm số đã cho là hàm số mũ với cơ số 2.

d) Hàm số y = x^{– 2} không phải là hàm số mũ.

HĐ2 trang 16 Toán 11 Tập 2

Nhận dạng đồ thị và tính chất của hàm số mũ

Cho hàm số mũ y = 2^x.

a) Hoàn thành bảng giá trị sau:

b) Trong mặt phẳng toạ độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; 2^x) với x ∈ ℝvà nối lại ta được đồ thị của hàm số y = 2^x.

c) Từ đồ thị đã vẽ ở câu b, hãy kết luận về tập giá trị và tính chất biến thiên của hàm số y = 2^x.

Lời giải:

a) Ta có: 2^{– 3} = $\frac{1}{8}$; 2^{– 2} = $\frac{1}{4}$; 2^{– 1} = $\frac{1}{2}$; 2⁰ = 1; 2¹ = 2; 2² = 4; 2³ = 8.

Vậy ta hoàn thành được bảng đã cho như sau:

b) Trên mặt phẳng tọa độ Oxy, ta biểu diễn các điểm (x; y) ở câu a và lấy thêm nhiều điểm (x; 2^x) với x ∈ ℝ, nối lại ta được đồ thị của hàm số y = 2^x như sau:

c) Từ đồ thị ở hình trên, ta thấy hàm số y = 2^x:

+ Có tập giá trị là (0; + ∞);

+ Đồng biến trên ℝ.

Toán 11 trang 17 Tập 2

Luyện tập trang 17 Toán 11 Tập 2:

Vẽ đồ thị của hàm số y=$\displaystyle y={{\left( {\frac{3}{2}} \right)}^{x}}$.

Lời giải:

Ta lập bảng giá trị của hàm số y= $\displaystyle y={{\left( {\frac{3}{2}} \right)}^{x}}$ tại một số điểm như sau:

Từ đó, ta vẽ được đồ thị hàm số y=(32)xy=32x như sau:

Toán 11 trang 18 Tập 2

HĐ3 trang 18 Toán 11 Tập 2:

Nhận biết hàm số lôgarit

a) Tính y = log₂x khi x lần lượt nhận các giá trị 1; 2; 4. Với mỗi giá trị của x > 0 có bao nhiêu giá trị của y = log₂x _­tương ứng?

b) Với những giá trị nào của x, biểu thức y = log₂x có nghĩa?

Lời giải:

a) Ta có:

+ Với x = 1 thì y = log₂1 = 0;

+ Với x = 2 thì y = log₂2 = 1;

+ Với x = 4 thì y = log₂4 = log₂2² = 2.

Nhận thấy với mỗi giá trị của x > 0 có duy nhất một giá trị của y = log₂x _­tương ứng.

b) Biểu thức y = log₂x có nghĩa khi x > 0.

Câu hỏi trang 18 Toán 11 Tập 2:

Trong các hàm số sau, những hàm số nào là hàm số lôgarit? Khi đó hãy chỉ ra cơ số

a) $\displaystyle y={{\log }_{{\sqrt{3}}}}x$

b) y= $\displaystyle {{\log }_{{{{2}^{{-2}}}}}}x$

c) y = log_x2;

d) $\displaystyle y={{\log }_{{\frac{1}{x}}}}5$

Lời giải

a) Hàm số $\displaystyle y={{\log }_{{\sqrt{3}}}}x$ là hàm số lôgarit với cơ số $\displaystyle \sqrt{3}$

b) Ta có y = $\displaystyle {{\log }_{{{{2}^{{-2}}}}}}x$ do đó hàm số đã cho là hàm số lôgarit với cơ số $\displaystyle \frac{1}{4}$

c) Hàm số y = log_x2 không phải hàm số lôgarit.

d) Hàm số $\displaystyle y={{\log }_{{\frac{1}{x}}}}5$

không phải hàm số lôgarit.

HĐ4 trang 18 Toán 11 Tập 2:

Nhận dạng đồ thị và tính chất của hàm số lôgarit

Cho hàm số lôgarit y = log₂x.

a) Hoàn thành bảng giá trị sau:

b) Trong mặt phẳng toạ độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; log₂x) và nối lại ta được đồ thị của hàm số y = log₂x.

c) Từ đồ thị đã vẽ ở câu b, hãy kết luận về tập giá trị và tính chất biến thiên của hàm số y = log₂x.

Lời giải:

a) Ta có log₂2^{– 3} = – 3; log₂2^{– 2} = – 2; log₂2^{– 1} = – 1; log₂1 = 0; log­₂2 = 1; log₂2² = 2; log₂2³ = 3. Vậy ta hoàn thành được bảng đã cho như sau:

b) Trên mặt phẳng tọa độ Oxy, ta biểu diễn các điểm (x; y) ở câu a và lấy thêm nhiều điểm (x; log₂x) với x > 0, nối lại ta được đồ thị của hàm số y = log₂x như sau:

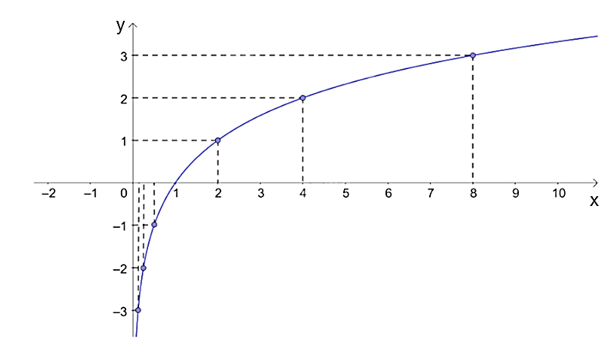
c) Từ đồ thị đã vẽ ở câu b, nhận thấy hàm số y = log₂x:

+ Có tập giá trị là ℝ;

+ Đồng biến trên (0; + ∞).

Toán 11 trang 19 Tập 2

Vận dụng trang 19 Toán 11 Tập 2

Giải bài toán trong tình huống mở đầu (kết quả tính theo đơn vị triệu người và làm tròn đến chữ số thập phân thứ hai).

Lời giải:

Theo bài ra ta có P = 97,34; r = 0,91%.

Từ năm 2020 đến năm 2050 là 30 năm nên t = 30.

Ước tính dân số Việt Nam vào năm 2050 là

A = Pe^rt = 97,34 ∙ e^{0,91% ∙ 30} ≈ 127,9 (triệu người).

Bài 6.15 trang 19 Toán 11 Tập 2

Vẽ đồ thị các hàm số sau:

a) y = 3^x;

b) $\displaystyle y={{\left( {\frac{1}{3}} \right)}^{x}}$

Lời giải:

a) y = 3^x

Ta lập bảng giá trị của hàm số y = 3^x tại một số điểm như sau:

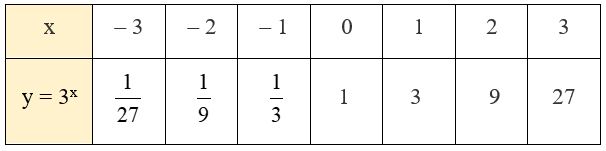
Từ đó, ta vẽ được đồ thị hàm số y = 3^x như sau:

b) $\displaystyle y={{\left( {\frac{1}{3}} \right)}^{x}}$

Ta lập bảng giá trị của hàm số $\displaystyle y={{\log }_{{\frac{1}{3}}}}x$

tại một số điểm như sau:

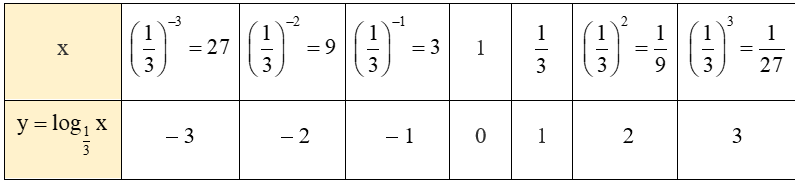
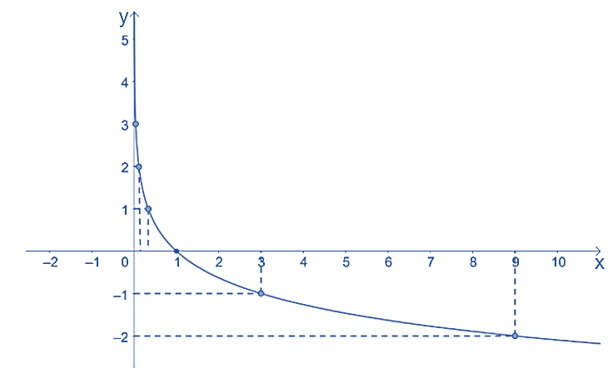
Từ đó, ta vẽ được đồ thị hàm số  $\displaystyle y={{\log }_{{\frac{1}{3}}}}x$

như sau:

Bài 6.16 trang 19 toán 11 tập 2

Vẽ đồ thị của các hàm số sau:

a) $y = \log x;$

b) $y = {\log _{\frac{1}{3}}}x.$

Lời giải chi tiết

a) Lập bảng giá trị của hàm số tại một điểm như sau:

Từ đó, ta vẽ được đồ thị của hàm số $y = \log x.$

b) Lập bảng giá trị của hàm số tại một điểm như sau:

Từ đó, ta vẽ được đồ thị của hàm số $y = {\log _{\frac{1}{3}}}x.$

Bài 6.17 trang 19 Toán 11 Tập 2:

Tìm tập xác định của các hàm số sau:

a) y = log|x + 3|;

b) y = ln(4 – x²).

Lời giải:

a) Biểu thức log|x + 3| xác định khi |x + 3| > 0.

Mà |x + 3| ≥ 0 với mọi x ∈ ℝ nên |x + 3| > 0 khi x + 3 ≠ 0, tức là x ≠ – 3.

Vậy tập xác định của hàm số y = |x + 3| là D = ℝ.

b) Biểu thức ln(4 – x²) xác định khi 4 – x² > 0 ⇔ x² < 4 ⇔ – 2 < x < 2.

Vậy tập xác định của hàm số y = ln(4 – x²) là D = (– 2; 2).

Bài 6.18 trang 19 Toán 11 Tập 2:

Giả sử một chất phóng xạ bị phân rã theo cách sao cho khối lượng m(t) của chất còn lại (tính bằng kilôgam) sau t ngày được cho bởi hàm số m(t) = 13e^{– 0,015t}.

a) Tìm khối lượng của chất đó tại thời điểm t = 0.

b) Sau 45 ngày khối lượng chất đó còn lại là bao nhiêu?

Lời giải:

m(0) = 13e⁰ = 13 (kg).

b) Sau 45 ngày, tức t = 45, khối lượng chất phóng xạ đó còn lại là

m(45) = 13e^{– 0,015 ∙ 45} ≈ 6,62 (kg).

Bài 6.19 trang 19 Toán 11 Tập 2:

Trong một nghiên cứu, một nhóm học sinh được cho xem cùng một danh sách các loài động vật và được kiểm tra lại xem họ còn nhớ bao nhiêu phần trăm danh sách đó sau mỗi tháng. Giả sử sau t tháng, khả năng nhớ trung bình của nhóm học sinh đó được tính theo công thức M(t) = 75 – 20ln(t + 1), 0 ≤ t ≤ 12 (đơn vị: %). Hãy tính khả năng nhớ trung bình của nhóm học sinh đó sau 6 tháng.

Lời giải:

Sau 6 tháng, tức là t = 6.

Khả năng nhớ trung bình của nhóm học sinh đó sau 6 tháng là

M(6) = 75 – 20ln(6 + 1) = 75 – 20ln7 ≈ 36,08%.