Giải toán 7 tập 2 trang 84 bài tập cuối chương 8
Giải toán 7 tập 2 trang 84 bài tập cuối chương 8
Giải toán 7 tập 2 trang 84 bài tập cuối chương 8 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 7 Chân trời sáng tạo. Mời các em học sinh cùng quý phụ huynh tham khảo.
Giải toán 7 tập 2 trang 84
Giải bài 1 trang 84 Toán 7 tập 2 CTST
Cho tam giác ABC cân tại $A (\widehat{A} < 90°)$. Hai đường cao BE và CF cắt nhau tại H.
a) Chứng minh rằng ∆BEC = ∆CFB.
b) Chứng minh rằng ∆AHF = ∆AHE.
c) Gọi I là trung điểm của BC. Chứng minh rằng ba điểm A, H, I thẳng hàng.
Hướng dẫn giải
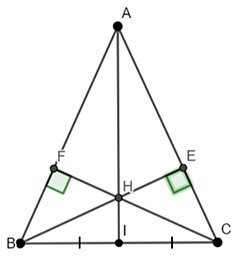
a) ∆ ABC cân tại $A => \widehat{ABC} = \widehat{ACB}$và AB = AC
$=> \widehat{FBC} = \widehat{ECB}$
BE và CF là hai đường cao của ∆ ABC
=> ∆BEC và ∆CFB là 2 tam giác vuông lần lượt tại E và F.
+ Xét ∆BEC vuông tại E và ∆CFB vuông tại F có:
BC chung
$\widehat{FBC} = \widehat{ECB}$
=> ∆BEC = ∆CFB (góc nhọn và một cạnh góc vuông)
b) Theo a: ∆BEC =∆CFB
=> EC = FB
Có AF = AB – FB
AE= AC – EC
Mà AB = AC, EC = FB
=> AF = AE
BE và CF là hai đường cao cắt nhau tại H
=> ∆AFH và ∆AEH là 2 tam giác vuông lần lượt tại F và E.
+ Xét ∆AFH vuông tại F và ∆AEH vuông tại E có:
AH chung
AF = AE
=> ∆AFH = ∆AEH (cạnh huyền và một cạnh góc vuông).
c) H là giao điểm của 2 đường cao BE và CF trong tam giác ABC
=> H là trực tâm của ∆ABC
=> AH ⊥ BC (1)
Có I là trung điểm của BC
=> AI là đường trung tuyến của ∆ ABC
Xét ∆ABI và ∆ACI có:
AB = AC
AI chung
IB = IC (I là trung điểm của BC)
=> ∆ABI = ∆ACI (c.c.c)
$=> \widehat{AIC} = \widehat{AIB}$
Có $\widehat{AIC} + \widehat{AIB} = 180°$
$=> 2\widehat{AIB} = 180°$
$=> \widehat{AIB} = 90°$
=> AI ⊥ BC (2)
Từ (1) và (2) => A, I, H thẳng hàng.
Giải bài 2 trang 84 Toán 7 tập 2 CTST
Cho tam giác ABC vuông tại A, vẽ đường cao AH. Trên tia đối của tia HA lấy điểm M sao cho H là trung điểm của AM.
a) Chứng minh tam giác ABM cân.
b) Chứng minh rằng ∆ABC = ∆MBC.
Hướng dẫn giải
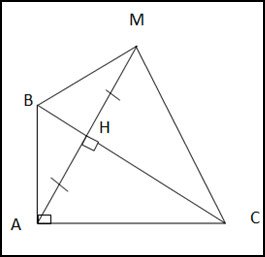
a) Có AH là đường cao của ∆ABC
=> AH ⊥ BC hay AM ⊥ BH
=> ∆BHA và ∆AHM là 2 tam giác vuông tại H
Xét ∆BHA và ∆BHM cùng vuông tại H có:
BH chung
AH = HM
=> ∆BHA = ∆BHM (hai cạnh góc vuông)
=> BA = BM
=> ∆ABM cân tại B.
b) Theo a: ∆BHA = ∆BHM
$=> \widehat{ABH} = \widehat{MBH}$hay $\widehat{ABC} = \widehat{MBC}$
Xét ∆ABC và ∆MBC có:
BC chung
$\widehat{ABC} = \widehat{MBC}$
AB = BM
=> ∆ABC = ∆MBC (c.g.c)
Giải bài 3 trang 84 Toán 7 tập 2 CTST
Cho tam giác ABC vuông tại A (AB, AC), vẽ đường cao AH. Trên tia đối của HC lấy điểm D sao cho HD = DC.
a) Chứng minh AC = AD.
b) Chứng minh rằng $\widehat{ADB} = \widehat{BAH}$
Hướng dẫn giải
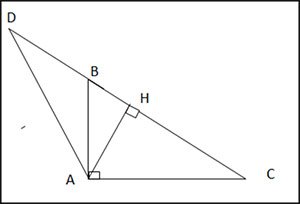
a) Ta có AH là đường cao của ∆ABC
=> ∆AHD và ∆AHC là 2 tam giác vuông tại H
Xét ∆AHD và ∆AHC cùng vuông tại H có:
AH chung
HD = HC
=> ∆AHD và ∆AHC (hai cạnh góc vuông)
=> AC = AD
b) + ∆ABC vuông tại A nên $\widehat{ABC} + \widehat{ACB}= 90°$
∆ABH vuông tại H nên $\widehat{ABH} + \widehat{HAB}= 90°$
$=> \widehat{ACB} = \widehat{HAB}$
+ Có AC = AD => ∆ ACD cân tại A
$=> \widehat{ACD} = \widehat{ADC}$
Mà $\widehat{ACB} = \widehat{HAB}$
$=> \widehat{ADB} = \widehat{HAB}$.
Giải bài 4 trang 84 Toán 7 tập 2 CTST
Cho tam giác vuông ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN. Kẻ BE ⊥ AN (E thuộc AN).
a) Chứng minh rằng BE là tia phân giác của góc ABN.
b) Kẻ đường cao AH của tam giác ABC. Gọi K là giao điểm của AH với BE. Chứng minh rằng NK // CA.
c) Đường thẳng BK cắt AC tại F. Gọi G là giao điểm của đường thẳng AB và NF. Chứng minh rằng tam giác GBC cân.
Hướng dẫn giải
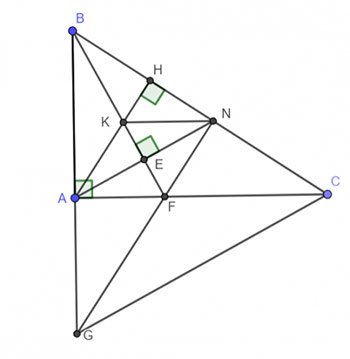
a) Xét ∆ABE và ∆NBE cùng vuông tại E có:
AB = BN
BE chung
=> ∆ABE = ∆NBE (cạnh huyền và một cạnh góc vuông).
$=> \widehat{ABE} = \widehat{NBE}$
=> BE là tia phân giác của góc ABN.
b) Xét tam giác ABN có: AH và BE là hai đường cao cắt nhau tại K
=> K là trực tâm tam giác ABN
=> NK ⊥ AB
mà AC ⊥ AB
=> NK // AC.
c) Xét ∆FBN và ∆ FBA có:
BN = BA
$\widehat{NBF} = \widehat{ABF}$(chứng minh trên)
BF chung
=> ∆FBN và ∆FBA (c.g.c)
mà ∆ FBA vuông tại A
=> ∆ FBN vuông tại N
=> BN ⊥ FN hay BN ⊥ GN
=> ∆ BNG vuông tại N
Xét 2 tam giác vuông ∆BNG và ∆BAC có
BN = BA
$\widehat{ABN}$chung
=> ∆BNG = ∆BAC (góc nhọn và một cạnh góc vuông)
=> BG = BC
=> ∆ BCG cân tại B.
Giải bài 5 trang 84 Toán 7 tập 2 CTST
Cho tam giác ABC nhọn (AB < AC), vẽ đường cao AH. Đường trung trực của cạnh BC cắt AC tại M, cắt BC tại N.
a) Chứng minh rằng $\widehat{BMN} = \widehat{HAC}$.
b) Kẻ MI ⊥ AH (I thuộc AH), gọi K là giao điểm của AH với BM. Chứng minh rằng I là trung điểm của AK.
Hướng dẫn giải
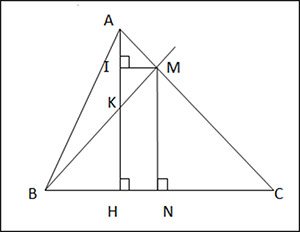
a) M, N thuộc đường trung trực của BC
=> MB = MC, NB = NC
=> ∆ MBC cân tại M, N là trung điểm của BC
=> MN là đường trung tuyến của ∆ MBC cân tại M
Xét ∆ MBN và ∆ MCN có:
MB = MC
BN = NC
MN chung
=> ∆ MBN = ∆ MCN (c.c.c)
$=> \widehat{BMN} = \widehat{CMN}$
∆ AHC vuông góc tại H
$=> \widehat{HAC} + \widehat{HCA} = 90°$
Hay $\widehat{MCN} + \widehat{HAC} = 90° (1)$
∆ MNC vuông góc tại N (MN là đường trung trực của BC)
$=> \widehat{MCN} + \widehat{NMC} = 90°$
Mà $\widehat{BMN} = \widehat{CMN}$
$=> \widehat{MCN} +\widehat{HAC} = 90° (2)$
Từ (1) và (2) ta có: $\widehat{HAC} = \widehat{BMN}$
b) Kẻ MI ⊥ AH
AH ⊥ BC
=> IM // BC
$=> \widehat{IMB} = \widehat{MBC}$(góc so le trong)
$\widehat{AMI} = \widehat{MCB}$(2 góc đồng vị)
Mà ∆MBC cân tại M nên $\widehat{MBC} = \widehat{MBC}$
$=> \widehat{IMB} = \widehat{AMI}$
Xét ∆MIK và ∆MIA cùng vuông tại I có:
MI chung
$\widehat{IMK} = \widehat{AMI}$(chứng minh trên)
=> ∆MIK = ∆MIA (góc nhọn và một cạnh góc vuông).
=> IK = IA
=> I là trung điểm của AK.
Giải bài 6 trang 84 Toán 7 tập 2 CTST
Cho tam giác nhọn MNP. Các trung tuyến ME và NF cắt nhau tại G. Trên tia đối của tia FN lấy điểm D sao cho FN = FD.
a) Chứng minh rằng ∆ MFN = ∆ PFD.
b) Trên đoạn thẳng FD lấy điểm H sao cho F là trung điểm của HG. Gọi K là trung điểm của PD. Chứng minh rằng 3 điểm M, H, K thẳng hàng.
Hướng dẫn giải
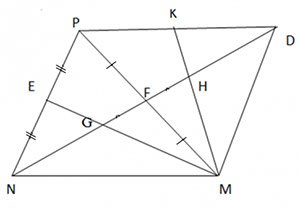
a) ME, NF là trung tuyến của ∆MNP
=> E là trung điểm của PN, F là trung điểm của PM
Xét ∆ MFN và ∆ PFD có
FN = FD
$\widehat{MFN} = \widehat{PFD}$(2 góc đối đỉnh)
FM = FP (F là trung điểm của PM)
=> ∆MFN = ∆PFD (c.g.c).
b)
+ Trong ∆MNP các trung tuyến ME và NF cắt nhau tại G.
=> G là trọng tâm của ∆MNP
$=> FG = \frac{1}{3} FN$
Mà FG = FH (F là trung điểm của HG); FN = FD
$=> FH = \frac{1}{3} FD => DH = \frac{2}{3} FD$
+ Xét tam giác PDM có: $DH = \frac{2}{3} FD$
Mà FD là đường trung tuyến của ∆PDM
=> H là trọng tâm của ∆PDM
=> MH là đường trung tuyến của ∆PDM (1)
K là trung điểm của PD
=> MK là đường trung tuyến của ∆PDM (2)
Từ (1) và (2)
=> M, H, K thẳng hàng.
Giải bài 7 trang 84 Toán 7 CTST
Cho tam giác ABC vuông tại A có $AB = \frac{1}{2} AC, AD$là tia phân giác của $\widehat{BAC}$(D thuộc BC). Gọi E là trung điểm của AC.
a) Chứng minh rằng DE = DB.
b) AB cắt DE tại K. Chứng minh rằng tam giác DCK cân và B là trung điểm của đoạn thẳng AK.
c) AD cắt CK tại H. Chứng minh rằng AH ⊥ CK.
Hướng dẫn giải
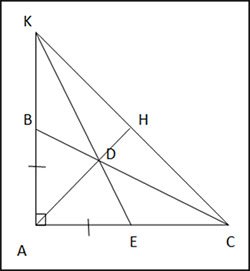
a) Xét ∆ABD và ∆AED có
AD chung
$\widehat{BAD} = \widehat{EAD}$(AD là đường phân giác)
AB = AE
=> ∆ ABD = ∆ AED (c.g.c)
=> BD = ED
b) + Chứng minh tam giác DCK cân.
Theo a: ∆ ABD = ∆ AED nên $\widehat{DBA} = \widehat{DEA}$
Ta có:
$\widehat{DBK} + \widehat{DBA} = 180°$
$\widehat{DEC} + \widehat{DEA} = 180°$
Mà $\widehat{DBA} = \widehat{DEA}$
$=> \widehat{DBK} = \widehat{DEC}$
Xét ∆CDE và ∆KDB có:
$\widehat{KDB} = \widehat{CDE}$(2 góc đối đỉnh)
DE = DB (chứng minh câu a)
$\widehat{DBK} = \widehat{DEC}$(chứng minh trên)
=> ∆CDE = ∆KDB (g.c.g)
=> DC = DK
=> ∆DCK cân tại D
+ Chứng minh B là trung điểm của đoạn thẳng AK.
Ta có: ∆CDE = ∆KDB nên EC = KB
Mà E là trung điểm của AC nên $EC = AE = \frac{1}{2} AC$
Mà $AB = \frac{1}{2} AC$
=> KB = AB
Mà A, B, K thẳng hàng
=> B là trung điểm của AK
c) B là trung điểm của AK
$=>AB = \frac{1}{2} AK$
Mà $AB = \frac{1}{2} AC$
=> AK = AC
Xét ∆KAH và ∆CAH có:
AK = AC
$\widehat{KAH} = \widehat{CAH}$(AD là đường phân giác của $\widehat{BAC}$)
AH chung
=> ∆KAH = ∆CAH (c.g.c)
$=> \widehat{AHK} = \widehat{AHC}$
Mà $\widehat{AHK} + \widehat{AHC} = 180°$
$=> 2\widehat{AHC} = 180°$
$=> \widehat{AHC} = 90°$
=> AH ⊥ HC hay AH ⊥ CK.
Giải bài 8 trang 84 Toán 7 CTST
Ở hình 1, cho biết AE = AF và $\widehat{ABC} = \widehat{ACB}$. Chứng minh rằng AH là đường trung trực của BC
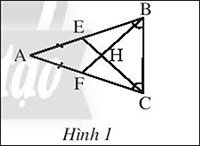
Hướng dẫn giải
$\widehat{ABC} = \widehat{ACB}$
=> ∆ ABC cân tại A
=> AB = AC
=> A thuộc đường trung trực của BC (1)
Ta có: FC = AC – AF
EB = AB – AE
Mà AB = AC, AE= AF
=> FC = CB
Xét ∆ FCB và ∆ EBC có:
BC chung
$\widehat{FCB} = \widehat{EBC}$
FC = CB (chứng minh trên)
=> ∆FCB = ∆EBC (c.g.c)
$=> \widehat{FBC} = \widehat{ECB}$
=> ∆HCB cân tại H
=> HC = HB
=> H thuộc đường trung trực của BC (2)
Từ (1) và (2) => AH là đường trung trực của BC.
Giải bài 9 trang 84 Toán 7 CTST
Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB tại M. Từ B kẻ BH vuông góc với đường thẳng CM (H thuộc CM). Trên tia đối của HC lấy điểm E sao cho HE = HM.
a) Chứng minh rằng tam giác MBE cân.
b) Chứng minh rằng $\widehat{EBH}= \widehat{ACM}$
c) Chứng minh rằng EB ⊥ BC.
Lời giải
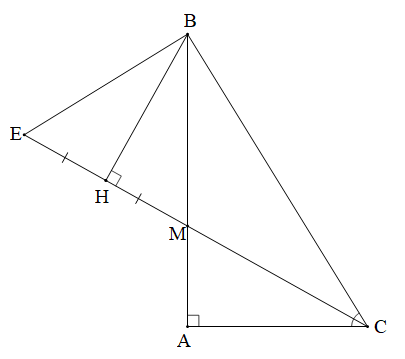
a)Xét $\Delta $BHE và $\Delta $BHM có :
BH là cạnh chung
EH = HM (do M đối xứng E qua H)
$\widehat {BHE} = \widehat {BHM} = {90^o}$
$\Rightarrow $$\Delta $BHE = $\Delta $BHM (c-g-c)
$\Rightarrow $BM = BE (cạnh tương ứng)
và $\widehat {EBH} = \widehat {MBH}$(góc tương ứng) (1)
$\Rightarrow $$\Delta $BEM cân tại B (2 cạnh bên bằng nhau)
b)Xét $\Delta $BHM vuông tại H $\Rightarrow \widehat {BMH} + \widehat {MBH} = {90^o}$
Xét $\Delta $AMC vuông tại A $\Rightarrow \widehat {AMC} + \widehat {MCA} = {90^o}$
Mà $\widehat {HMB} = \widehat {AMC}$(2 góc đối đỉnh)
$\Rightarrow \widehat {MCA} = \widehat {MBH} = {90^o} – \widehat {AMC} = {90^o} – \widehat {HMB}$(2)
Từ (1) và (2) $\Rightarrow \widehat {EBH} = \widehat {ACM}$
c)Vì $\widehat {BCM} = \widehat {ACM}$(do CM là phân giác góc C)
$\Rightarrow \widehat {EBH} = \widehat {BCM}$(cùng bằng $\widehat {AMC}$) (3)
Xét $\Delta $EHB vuông tại H có $\widehat {EBH} + \widehat {BEH} = {90^o}$(4)
Từ (3) và (4) $\Rightarrow \widehat {BCM} + \widehat {BEH} = {90^o}$
$\Rightarrow \widehat {EBC} = {90^o} \Rightarrow EB \bot BC$
Giải bài 10 trang 84 Toán 7 tập 2 CTST
Trên đường thẳng a lấy 3 điểm phân biệt I, J, K (J ở giữa I và K). Kẻ đường thẳng b vuông góc với a tại J, trên b lấy điểm M khác điểm J. Đường thẳng qua I vuông góc với MK cắt b tại N. Chứng minh rằng KN vuông góc với MI.
Hướng dẫn giải
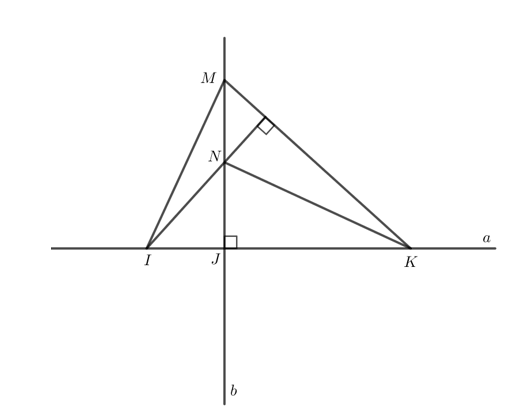
Vì b vuông góc với a tại J (theo giả thiết) và M thuộc b
$\Rightarrow MJ \bot IK$(1)
Vì đường thẳng qua I vuông góc với MK và cắt b tại N (gọi C là giao của MK và đường thẳng qua I vuông góc với MK)
$\Rightarrow MK \bot IC$(2)
Từ (1) và (2)$\Rightarrow $N là trực tâm ΔMIK
$\Rightarrow $NK là đường cao của ΔMIK (Các đường cao trong tam giác đi qua trực tâm)
$\Rightarrow $KN $\bot $MI
