Giải toán 8 tập 2 trang 28 Bài tập cuối chương 5

Giải toán 8 tập 2 trang 28 bài tập cuối chương 5 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 8 CTST. Mời các em học sinh cùng quý phụ huynh tham khảo.

Giải toán 8 tập 2 trang 28

Bài 1 trang 28 toán 8 tập 2

Vẽ một hệ trục tọa độ Oxy và đánh dấu các điểm M(1; 1), N(4; 1), P(2; −1), Q(−1; −1). Tứ giác MNPQ là hình gì?

A. Hình bình hành;

B. Hình thang cân;

C. Hình vuông;

D. Hình chữ nhật

Gợi ý đáp án

Đáp án đúng là: A

Từ đồ thị hàm số ta thấy tứ giác MNPQ là hình bình hành.

Ta biểu diễn các điểm $M\left( {1;1} \right);N\left( {4;1} \right);P\left( {2; – 1} \right);Q\left( { – 1; – 1} \right)$ trên hệ trục tọa độ ta được:

Từ hình vẽ ta thấy, độ dài đoạn thẳng $MN = 3;QP = 3$

Lại có: $MN//Ox;QP//Ox \Rightarrow MN//QP$.

Tứ giác $MNPQ$ có: $MN//PQ;MN = PQ \Rightarrow $ tứ giác $MNPQ$ là hình bình hành.

Bài 2 trang 28 toán 8 tập 2

Độ dài cạnh $MN$ của tứ giác trong câu 1 là

A. 3.                     B. 5.                     C. $\sqrt 3 $.                 D. $\sqrt 5 $.

Gợi ý đáp án

Đáp án đúng là: A

Ta có: $M\left( {1;1} \right);N\left( {4;1} \right) \Rightarrow MN = \left| {1 – 4} \right| = 3$.

Bài 3 trang 28 toán 8 tập 2

Một người bắt đầu mở một vòi nước vào một bể đã chữa sẵn 2 m3 nước, mỗi giờ chảy được 3 m3 nước. Thể tích y(m3) của nước có trong bể sau x giờ bằng:

A. y = 2x + 3;

B. y = 3x + 2;

C. y = 6x;

D. y = x +6.

Gợi ý đáp án

Đáp án đúng là: B

Ta có y = 2x + 3.

Bài 4 trang 28 toán 8 tập 2

Trong các điểm sau, điểm nào thuộc đồ thị của hàm số $y = 2 – 4x$?

A. $\left( {1;1} \right)$.

B. $\left( {2;0} \right)$.

C. $\left( {1; – 1} \right)$.

D. $\left( {1; – 2} \right)$.

Gợi ý đáp án

Đáp án đúng là D

+ Xét điểm $\left( {1;1} \right)$ ta có: $y = 2 – 4.1 =  – 2 \ne 1$. Do đó, điểm $\left( {1;1} \right)$không thuộc đồ thị hàm số.

+ Xét điểm $\left( {2;0} \right)$ ta có: $y = 2 – 4.2 =  – 6 \ne 2$. Do đó, điểm $\left( {2;0} \right)$không thuộc đồ thị hàm số.

+ Xét điểm $\left( {1; – 1} \right)$ ta có: $y = 2 – 4.1 =  – 2 \ne  – 1$. Do đó, điểm $\left( {1; – 1} \right)$không thuộc đồ thị hàm số.

+ Xét điểm $\left( {1; – 2} \right)$ ta có: $y = 2 – 4.1 =  – 2$. Do đó, điểm $\left( {1; – 2} \right)$ thuộc đồ thị hàm số.

Bài 5 trang 28 Toán 8 Tập 2:

Trong các điểm sau điểm nào thuộc đồ thị cảu hàm số y = −5x + 5?

A.(1; 1);

B. (2; 0);

C. (0; 4);

D. (2; −5).

Gợi ý đáp án

Đáp án đúng là D

+ Xét điểm $\left( {1;1} \right)$ ta có: $y =  – 5.1 + 5 = 0 \ne 1$. Do đó, điểm $\left( {1;1} \right)$không thuộc đồ thị hàm số.

+ Xét điểm $\left( {2;0} \right)$ ta có: $y =  – 5.2 + 5 =  – 5 \ne 0$. Do đó, điểm $\left( {2;0} \right)$không thuộc đồ thị hàm số.

+ Xét điểm $\left( {0;4} \right)$ ta có: $y =  – 5.0 + 5 = 5 \ne 4$. Do đó, điểm $\left( {0;4} \right)$không thuộc đồ thị hàm số.

+ Xét điểm $\left( {2; – 5} \right)$ ta có: $y =  – 5.2 + 5 =  – 5$. Do đó, điểm $\left( {2; – 5} \right)$ thuộc đồ thị hàm số.

.

Bài 6 trang 28 toán 8 tập 2

Đường thẳng song song với đường thẳng $y = 2x$ và cắt trục tung tại điểm có tung độ bằng 1 là:

A. $y = 2x – 1$.   B. $y =  – 2x – 1$. C. $y = 2x + 1$.  D. $y = 6 – 2\left( {1 – x} \right)$.

Gợi ý đáp án

Đáp án đúng là C

Gọi đường thẳng cần tìm là $d:y = ax + b$.

Vì đường thẳng $d$ song song với đường thẳng $y = 2x$ nên $\left\{ \begin{array}{l}a = 2\\b \ne 0\end{array} \right.$

Lại có, đường thẳng $d$ cắt trục tung tại điểm có tung độ bằng 1 nên đường thẳng $d$ đi qua điểm $A\left( {0;1} \right)$. Do đó, $b = 1 \ne 0$ (thỏa mãn).

Vậy đường thẳng $d$ cần tìm là $y = 2x + 1$.

Bài 7 trang 28 toán 8 tập 2

Cho hai đường thẳng $y = \dfrac{1}{2}x + 3$ và $y =  – \dfrac{1}{2}x + 3$. Hai đường thẳng đã cho

A. Cắt nhau tại điểm có hoành độ là 3.

B. Song song với nhau.

C. Cắt nhau tại điểm có tung độ là 3.

D. trùng nhau.

Gợi ý đáp án

Đáp án đúng là C

Đường thẳng $y = \dfrac{1}{2}x + 3$ có hệ số góc là $a = \dfrac{1}{2}$; Đường thẳng $y =  – \dfrac{1}{2}x + 3$ có hệ số góc là $a = \dfrac{{ – 1}}{2}$. Do đó, hai đường thẳng này cắt nhau.

Lại có:  Đường thẳng $y = \dfrac{1}{2}x + 3$ cắt trục tung tại điểm $A\left( {0;3} \right)$; Đường thẳng $y =  – \dfrac{1}{2}x + 3$ cắt trục tung tại điểm $A\left( {0;3} \right)$. Do đó, $A$ là giao điểm của hai đường thẳng.

Hoành độ điểm $A$ là $x = 0$; tung độ của điểm $A$ là $y = 3$.

Bài 8 trang 28 toán 8 tập 2

Cho các hàm số bậc nhất: $y = \dfrac{1}{3}x + 2$; $y =  – \dfrac{1}{3}x + 2$;$y =  – 3x + 2$. Kết luận nào sau đây đúng?

A. Đồ thị của các hàm số trên là các đường thẳng song song với nhau.

B. Đồ thị của các hàm số trên là các đường thẳng đi qua gốc tọa độ.

C. Đồ thị của các hàm số trên là các đường thẳng trùng nhau.

D. Đồ thị của các hàm số trên là các đường thẳng cắt nhau tại một điểm.

Gợi ý đáp án

Đáp án đúng là D

– Đồ thị hàm số $y = \dfrac{1}{3}x + 2$ là đường thẳng có hệ số góc là $a = \dfrac{1}{3}$.

– Đồ thị hàm số  $y =  – \dfrac{1}{3}x + 2$ là đường thẳng có hệ số góc là $a =  – \dfrac{1}{3}$.

– Đồ thị hàm số $y =  – 3x + 2$ là đường thẳng có hệ số góc là $a =  – 3$.

Vì cả ba đường thẳng đều có hệ số góc khác nhau nên chúng cắt nhau.

– Đồ thị hàm số $y = \dfrac{1}{3}x + 2$ cắt trục tung tại điểm $A\left( {0;2} \right)$.

– Đồ thị hàm số $y =  – \dfrac{1}{3}x + 2$ cắt trục tung tại điểm $A\left( {0;2} \right)$

– Đồ thị hàm số $y =  – 3x + 2$ cắt trục tung tại điểm $A\left( {0;2} \right)$

Do đó điểm $A\left( {0;2} \right)$ là giao điểm của ba đồ thị hàm số.

Vậy đồ thị của các hàm số trên là các đường thẳng cắt nhau tại một điểm.

Bài 9 trang 28 toán 8 tập 2

Đồ thị hàm số $y = \dfrac{{ – x + 10}}{5}$

A. là một đường thẳng có hệ số góc là -1.

B. không phải là một đường thẳng.

C. cắt trục hoành tại điểm có hoành độ là 10.

D. đi qua điểm $\left( {200;50} \right)$.

Gợi ý đáp án

Đáp án đúng là C

Ta có: $y = \dfrac{{ – x + 10}}{5} = \dfrac{{ – x}}{5} + \dfrac{{10}}{5} = \dfrac{{ – 1}}{5}x + 2$

Vì hàm số $y = \dfrac{{ – 1}}{5}x + 2$ có dạng $y = ax + b$ nên đồ thị của hàm số là một đường thẳng với hệ số góc $a = \dfrac{{ – 1}}{5}$.

Đồ thị hàm số cắt trục tung tại điểm $A\left( {0;2} \right)$; Đồ thị hàm số cắt trục hoành tại điểm $B\left( {10;0} \right)$.

Thay $x = 200$ vào hàm số ta được: $y = \dfrac{{ – 1}}{5}.200 + 2 =  – 40 + 2 =  – 38 \ne 50$. Do đó điểm $\left( {200;50} \right)$không thuộc đồ thị hàm số.

Vậy đáp án đúng là đồ thị hàm số cắt trục hoành tại điểm có hoành độ là 10.

Bài 10 trang 28 toán 8 tập 2

Cho hàm số $y = f\left( x \right) = \dfrac{5}{{4x}}$.

a) Tính $f\left( {\dfrac{1}{5}} \right);f\left( { – 5} \right);f\left( {\dfrac{4}{5}} \right)$.

b) Hãy tìm các giá trị tương ứng của hàm số trong bảng sau:

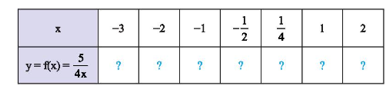
Hướng dẫn giải

a) Ta có:

$f\left( {\dfrac{1}{5}} \right) = \dfrac{5}{{4.\dfrac{1}{5}}} = \dfrac{5}{{\dfrac{4}{5}}} = 5:\dfrac{4}{5} = 5.\dfrac{5}{4} = \dfrac{{25}}{4};$

$f\left( { – 5} \right) = \dfrac{5}{{4.\left( { – 5} \right)}} = \dfrac{5}{{ – 20}} = \dfrac{{ – 1}}{4};$

$f\left( {\dfrac{4}{5}} \right) = \dfrac{5}{{4.\dfrac{4}{5}}} = \dfrac{5}{{\dfrac{{16}}{5}}} = 5:\dfrac{{16}}{5} = 5.\dfrac{5}{{16}} = \dfrac{{25}}{{16}}$

b) Ta có:

$f\left( { – 3} \right) = \dfrac{5}{{4.\left( { – 3} \right)}} = \dfrac{5}{{ – 12}} = \dfrac{{ – 5}}{{12}};$

$f\left( { – 2} \right) = \dfrac{5}{{4.\left( { – 2} \right)}} = \dfrac{5}{{ – 8}} = \dfrac{{ – 5}}{8};$

$f\left( { – 1} \right) = \dfrac{5}{{4.\left( { – 1} \right)}} = \dfrac{5}{{ – 4}} = \dfrac{{ – 5}}{4};$

$f\left( { – \dfrac{1}{2}} \right) = \dfrac{5}{{4.\left( { – \dfrac{1}{2}} \right)}} = \dfrac{5}{{\dfrac{{ – 4}}{2}}} = \dfrac{5}{{ – 2}} = \dfrac{{ – 5}}{2}$;

$f\left( {\dfrac{1}{4}} \right) = \dfrac{5}{{4.\dfrac{1}{4}}} = \dfrac{5}{{\dfrac{4}{4}}} = \dfrac{5}{1} = 5$;

$f\left( 1 \right) = \dfrac{5}{{4.1}} = \dfrac{5}{4}$;

$f\left( 2 \right) = \dfrac{5}{{4.2}} = \dfrac{5}{8}$

Ta có bảng sau:

Giải toán 8 tập 2 trang 29

Bài 11 trang 29 toán 8 tập 2

Cho hàm số $y = f\left( x \right) =  – {x^2} + 1$. Tính $f\left( { – 3} \right);f\left( { – 2} \right);f\left( { – 1} \right);f\left( 0 \right);f\left( 1 \right)$.

Hướng dẫn giải

$f\left( { – 3} \right) =  – {\left( { – 3} \right)^2} + 1 =  – 9 + 1 =  – 8$;

$f\left( { – 2} \right) =  – {\left( { – 2} \right)^2} + 1 =  – 4 + 1 =  – 3$;

$f\left( { – 1} \right) =  – {\left( { – 1} \right)^2} + 1 =  – 1 + 1 = 0$;

$f\left( 0 \right) =  – {0^2} + 1 = 0 + 1 = 1$;

$f\left( 1 \right) =  – {1^2} + 1 =  – 1 + 1 = 0$;

Bài 12 trang 29 toán 8 tập 2

Vẽ một hệ trục tọa độ $Oxy$ và đánh dấu các điểm $A\left( { – 2;0} \right);B\left( {0;4} \right);C\left( {5;4} \right);D\left( {3;0} \right)$. Tứ giác $ABCD$ là hình gì?

Hướng dẫn giải

$A\left( { – 2;0} \right)$ $ \Rightarrow $ hoành độ của điểm $A$ là –2 và tung độ của điểm $A$ là 0.

$B\left( {0;4} \right)$ $ \Rightarrow $ hoành độ của điểm $B$ là 0 và tung độ của điểm $B$ là 4.

$C\left( {5;4} \right)$ $ \Rightarrow $ hoành độ của điểm $C$ là 5 và tung độ của điểm $C$ là 4.

$D\left( {3;0} \right)$ $ \Rightarrow $ hoành độ của điểm $D$ là 3 và tung độ của điểm $D$ là 0.

Biểu diễn các điểm $A;B;C;D$ trên mặt phẳng tọa độ ta được:

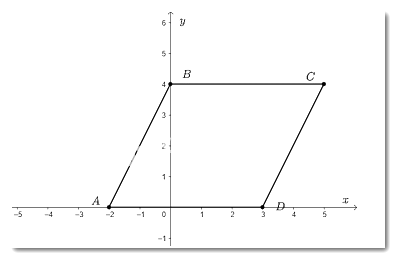
Vì hai điểm $B;C$ có tung độ bằng nhau nên $BC$ song song với $Ox$; Hai điểm $A;D$ có tung độ bằng nhau nên $AD$ song song với $Ox$.

Do đó, $BC//AD$.

Lại có, $AD = \left| {3 – \left( { – 2} \right)} \right| = 5;BC = \left| {5 – 0} \right| = 5$. Do đó, $AD = BC$.

Xét tứ giác $ABCD$có:

$AD = BC$

$BC//AD$

Do đó, tứ giác $ABCD$ là hình bình hành.

Bài 13 trang 29 Toán 8 Tập 2:

Cho biết đồ thị của hàm số y = ax đi qua điểm $P\left( {1; – \dfrac{4}{5}} \right)$.

a) Xác định hệ số a.

b) Vẽ điểm trên đồ thị có hoành độ bằng −5.

c) Vẽ điểm trên đồ thị có tung độ bằng 2.

Lời giải:

a) a) Vì đồ thị hàm số đi$y = ax$ đi qua điểm $P\left( {1; – \dfrac{4}{5}} \right)$ nên ta có:

$\dfrac{{ – 4}}{5} = a.1 \Rightarrow a = \dfrac{{ – 4}}{5}$.

Vậy hệ số góc của đường thẳng là $a = \dfrac{{ – 4}}{5}$.

b) Ta có: x = −5 suy ra y = 4, ta xác định được điểm A(−5; 4).

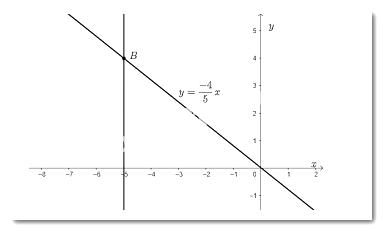
c) Từ điểm $y = 2$ trên $Oy$vẽ đường thẳng vuông góc với $Oy$ cắt đồ thị hàm số tại điểm $C$. Khi đó, điểm $C$ là điểm trên đồ thị hàm số có tung độ bằng 2.

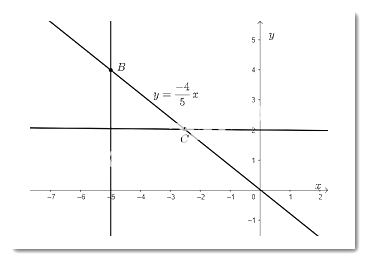
Bài 14 trang 29 Toán 8 Tập 2:

Tìm hàm số có đồ thị là đường thẳng song song với đồ thị hàm số y = −2x + 10.

Lời giải:

Hàm số có đồ thị là đường thẳng song song với đồ thị hàm số y = −2x + 10 là các hàm số có dạng y = ax + b với a = −2 và b ≠ 10.

Bài 15 trang 29 Toán 8 Tập 2:

Một người đi bộ với tốc độ không đổi 3 km/ h. Gọi s (km) là quãng đường đi được trong t (giờ).

a) Lập công thức tính s theo t.

b) Vẽ đồ thị của hàm số s theo biến số t.

Lời giải:

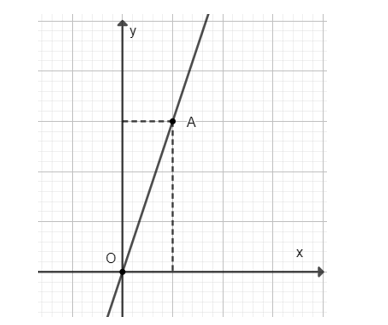
a) Công thức: s = 3t

b) Với t = 1 thì s = 3

Đồ thị hàm số s = 3t đi qua O(0; 0) và A(1; 3):

Bài 16 trang 29 Toán 8 Tập 2:

Tìm m để các hàm số bậc nhất y = 2mx – 2 và y = 6x + 3 có đồ thị là những đường thẳng song song với nhau.

Lời giải:

y = 2mx – 2 và y = 6x + 3 song song với nhau nên 2m = 6 suy ra m = 3.

Vậy với m = 3 thì thỏa mãn yêu cầu bài toán.

Bài 17 trang 29 Toán 8 Tập 2:

Tìm n để các hàm số bậc nhất y = 3nx + 4 và y = 6x + 4 có đồ thị là những đường thẳng trùng nhau.

Lời giải:

y = 3nx + 4 và y = 6x + 4 trùng nhau nên 3n = 6 suy ra n = 2.

Bài 18 trang 29 Toán 8 Tập 2:

Tìm k để các hàm số bậc nhất y = kx – 1 và y = 4x + 1 có đồ thị là những đường thẳng cắt nhau.

Lời giải:

y = kx – 1 và y = 4x + 1 có đồ thị là những đường thẳng cắt nhau nên k ≠ 4.

Bài 19 trang 29 Toán 8 Tập 2:

Cho hai hàm số y = x + 3, y = −x + 3 có đồ thị lần lượt là các đường thẳng d₁ và d₂.

a) Bằng cách vẽ hình, tìm tọa độ giao điểm A của hai đường thẳng nói trên và tìm các giao điểm B, C lần lượt của d₁ và d₂ với trục Ox.

b) Dùng thước đo góc để tìm góc tạo bởi d₁ và d₂ lần lượt với trục Ox.

c) Tính chu vi và diện tích của tam giác ABC.

Lời giải:

a) Với hàm số y = x + 3

Cho x = 0 thì y = 3

Cho y = 0 thì x = −3

Đồ thị hàm số y = x + 3 đi qua (0; 3) và B(−3; 0)

Với hàm số y = −x + 3

Cho x = 0 thì y = 3

Cho y = 0 thì x = 3

Đồ thị hàm số y = -x +3 đi qua A(0; 3) và C(3; 0)

Ta có A (0; 3) là giao điểm của hai đường thẳng nói trên và B(−3; 0), C(3; 0) lần lượt của d₁ và d₂ với trục Ox.

b) Góc tạo bởi d₁ và Ox bằng 45°, góc tạo bởi d₂ và Ox bằng 135°.

Hướng dẫn giải:

Gọi ${\alpha _1};{\alpha _2}$ lần lượt là 2 góc tạo bởi đường thẳng ${d_1};{d_2}$ với $Ox$.

Dùng thước đo độ ta kiểm tra được${\alpha _1} = 45^\circ ;{\alpha _2} = 135^\circ $.

c)

c) Tính chu vi và diện tích của tam giác $ABC$.

Hướng dẫn giải:

Vì $Ox \bot Oy$ tại $O$nên tam giác $AOB$ và tam giác $AOC$ đều vuông tại $O$.

Ta có: $OA = 3;OB = 3;OC = 3$

$BC = OB + OC = 3 + 3 = 6$.

Áp dụng định lí Py – ta – go cho tam giác $AOB$ ta có:

$O{A^2} + O{B^2} = A{B^2}$

$ \Leftrightarrow {3^2} + {3^2} = A{B^2}$

$ \Leftrightarrow A{B^2} = 9 + 9 = 18$

$ \Leftrightarrow AB = \sqrt {18}  = 3\sqrt 2 $

Áp dụng định lí Py – ta – go cho tam giác $AOC$ ta có:

$O{A^2} + O{C^2} = A{C^2}$

$ \Leftrightarrow {3^2} + {3^2} = A{C^2}$

$ \Leftrightarrow A{C^2} = 9 + 9 = 18$

$ \Leftrightarrow AC = \sqrt {18}  = 3\sqrt 2 $

Chu vi tam giác $ABC$ là:

$C = AB + AC + BC = 3\sqrt 2  + 3\sqrt 2  + 6 = 6 + 6\sqrt 2 $ (đơn vị độ dài)

Vì $Ox \bot Oy$ nên $OA$ vuông góc với $BC$ tại $O$. Do đó, $OA$ là đường cao  tam giác $ABC$ ứng với cạnh $BC$.

Diện tích tam giác $ABC$ là:

$S = \dfrac{1}{2}OA.BC = \dfrac{1}{2}.3.6 = 9$ (đơn vị diện tích)

Vậy chu vi tam giác $ABC$ là $6 + 6\sqrt 2 $ đơn vị độ dài và diện tích tam giác $ABC$ là 9 đơn vị diện tích.