Giải toán 8 tập 2 trang 76 Bài 3: Các trường hợp đồng dạng của hai tam giác vuông
Giải toán 8 tập 2 trang 76 Bài 3: Các trường hợp đồng dạng của hai tam giác vuông
Giải toán 8 tập 2 trang 76 bài 3 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 8 CTST. Mời các em học sinh cùng quý phụ huynh tham khảo.
Giải toán 8 tập 2 trang 73
Mở đầu trang 73 toán 8 tập 2
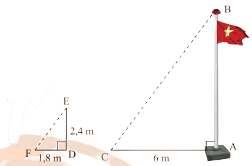
Bóng của một cột cờ trên mặt đất dài 6m. Cùng thời điểm đó một thanh sắt cao 2,4m cắm vuông góc với mặt đất có bóng dài 1,8m. Tính chiều cao của cột cờ.
Hướng dẫn giải
Cùng một thời điểm thì góc tạo bởi tia nắng và mặt đất là như nhau. Do đó, $\widehat {EFD} = \widehat {BCA}$.
Xét tam giác $DEF$ và tam giác $ABC$ ta có:
$\widehat {EFD} = \widehat {BCA}$ (chứng minh trên)
$\widehat {EDF} = \widehat {BAC} = 90^\circ $.
Do đó, $\Delta DEF\backsim\Delta ABC$ (g.g)
Suy ra, $\frac{{FD}}{{AC}} = \frac{{ED}}{{AB}} \Leftrightarrow \frac{{1,8}}{6} = \frac{{2,4}}{{AB}} \Rightarrow AB = \frac{{6.2,4}}{{1,8}} = 8$.
Vậy cột cờ $AB$ cao 8m.
Khám phá 1 trang 73 toán 8 tập 2
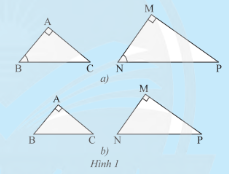
a) Từ trường hợp đồng dạng thứ ba của hai tam giác, xét xem tam giác $ABC$ vuông tại $A$ và tam giác $MNP$ vuông tại $M$ có $\widehat B = \widehat N$ thì hai tam giác đó có đồng dạng với nhau không.
b) Từ trường hợp đồng dạng thứ hai của hai tam giác, xét xem nếu tam giác $ABC$ vuông tại $A$ và tam giác $MNP$ vuông tại $M$ có $\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}$ thì hai tam giác đó có đồng dạng với nhau không.
Hướng dẫn giải:
a) Xét tam giác $ABC$ và tam giác $MNP$ ta có:
$\widehat B = \widehat N$ (giả thuyết)
$\widehat A = \widehat M = 90^\circ $.
Do đó, $\Delta ABC\backsim\Delta MNP$ (g.g)
b) Xét tam giác $ABC$ và tam giác $MNP$ ta có:
$\frac{{AB}}{{MN}} = \frac{{AC}}{{MP}}$ (giả thuyết)
$\widehat A = \widehat M = 90^\circ $.
Do đó, $\Delta ABC\backsim\Delta MNP$ (c.g.c).
Thực hành 1 trang 73 toán 8 tập 2
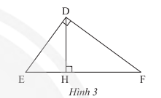
Cho tam giác $DEF$ vuông tại $D$ có $DH$ là đường cao (Hình 3). Chứng minh rằng $D{E^2} = EH.EF$
Hướng dẫn giải:
Vì $DH \bot EF \Rightarrow \widehat {DHE} = 90^\circ $
Xét tam giác $DEH$ và tam giác $FED$ ta có:
$\widehat E$ chung
$\widehat {DHE} = \widehat {EDF} = 90^\circ $.
Do đó, $\Delta DEH\backsim\Delta FED$ (g.g)
Suy ra, $\frac{{DE}}{{EF}} = \frac{{EH}}{{DE}} \Rightarrow D{E^2} = EF.EH$ (điều phải chứng minh).
Giải toán 8 tập 2 trang 74
Vận dụng 1 trang 74 toán 8 tập 2
Tính chiều cao của cột cờ trong hoạt động khởi động trang 73.
Hướng dẫn giải:

Cùng một thời điểm thì góc tạo bởi tia nắng và mặt đất là như nhau. Do đó, $\widehat {EFD} = \widehat {BCA}$.
Xét tam giác $DEF$ và tam giác $ABC$ ta có:
$\widehat {EFD} = \widehat {BCA}$ (chứng minh trên)
$\widehat {EDF} = \widehat {BAC} = 90^\circ $.
Do đó, $\Delta DEF\backsim\Delta ABC$ (g.g)
Suy ra, $\frac{{FD}}{{AC}} = \frac{{ED}}{{AB}} \Leftrightarrow \frac{{1,8}}{6} = \frac{{2,4}}{{AB}} \Rightarrow AB = \frac{{6.2,4}}{{1,8}} = 8$.
Vậy cột cờ $AB$ cao 8m.
Khám phá 2 trang 74 toán 8 tập 2
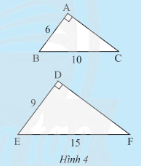
Cho hai tam giác vuông $ABC$ và $DEF$ có các kích thước như Hình 4.
a) Hãy tính độ dài cạnh $AC$ và $DF$.
b) So sánh các tỉ số $\frac{{AB}}{{DE}};\frac{{AC}}{{DF}}$ và $\frac{{BC}}{{EF}}$.
c) Dự đoán sự đồng dạng của hai tam giác$ABC$ và $DEF$.
Hướng dẫn giải:
a) Xét tam giác $ABC$ vuông tại $A$ ta có:
$A{B^2} + A{C^2} = B{C^2}$ (định lí Py – ta – go)
$ \Leftrightarrow {6^2} + A{C^2} = {10^2} \Leftrightarrow A{C^2} = {10^2} – {6^2} = 64 \Leftrightarrow AC = 8$.
Xét tam giác $DEF$ vuông tại $D$ ta có:
$D{E^2} + D{F^2} = E{F^2}$ (định lí Py – ta – go)
$ \Leftrightarrow {9^2} + D{F^2} = {15^2} \Leftrightarrow D{F^2} = {15^2} – {9^2} = 144 \Leftrightarrow DF = 12$.
b) Tỉ số:
$\frac{{AB}}{{DE}} = \frac{6}{9} = \frac{2}{3};\frac{{AC}}{{DF}} = \frac{8}{{12}} = \frac{2}{3}$; $\frac{{BC}}{{EF}} = \frac{{10}}{{15}} = \frac{2}{3}$.
Do đó, $\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}$.
c) Xét tam giác$ABC$ và tam giác$DEF$ có:
$\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{3}$ (chứng minh trên)
Do đó, $\Delta ABC\backsim\Delta DEF$ (c.c.c)
Thực hành 2 trang 74 toán 8 tập 2
Trong Hình 6, tam giác nào đồng dạng với tam giác $DEF$?
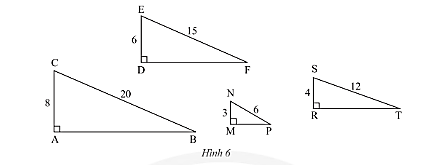
Hướng dẫn giải:
Tỉ số:
$\frac{{DE}}{{AC}} = \frac{6}{8} = \frac{3}{4};\frac{{EF}}{{BC}} = \frac{{15}}{{20}} = \frac{3}{4}$.
Xét tam giác$DEF$ và tam giác$ABC$ có:
$\frac{{DE}}{{AC}} = \frac{{EF}}{{BC}} = \frac{3}{4}$ (chứng minh trên)
Do đó, $\Delta DEF\backsim\Delta ABC$.
Tỉ số:
$\frac{{DE}}{{MN}} = \frac{6}{3} = 2;\frac{{EF}}{{NP}} = \frac{{15}}{6} = \frac{5}{2}$.
Vì $\frac{{DE}}{{MN}} \ne \frac{{EF}}{{NP}}$ nên hai tam giác $DEF$ và $MNP$ không đồng dạng với nhau.
Tỉ số:
$\frac{{DE}}{{RS}} = \frac{6}{4} = \frac{3}{2};\frac{{EF}}{{ST}} = \frac{{15}}{{12}} = \frac{5}{4}$.
Vì $\frac{{DE}}{{RS}} \ne \frac{{EF}}{{ST}}$ nên hai tam giác $DEF$ và $SRT$ không đồng dạng với nhau.
Giải toán 8 tập 2 trang 75
VậN DụNG 2 trang 75 toán 8 tập 2
Trong Hình 7, biết $\Delta MNP\backsim\Delta ABC$ với tỉ số đồng dạng $k = \frac{{MN}}{{AB}}$, hai đường cao tương ứng là $MK$ và $AH$.
a) Chứng minh rằng $\Delta MNK\backsim\Delta ABH$và $\frac{{MK}}{{AH}} = k$.
b) Gọi ${S_1}$ là diện tích tam giác $MNP$ và ${S_2}$ là diện tích tam giác $ABC$. Chứng minh rằng $\frac{{{S_1}}}{{{S_2}}} = {k^2}$.
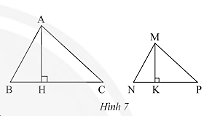
Hướng dẫn giải:
a) Vì tam giác $\Delta MNP\backsim\Delta ABC$ nên $\widehat B = \widehat N$ (hai góc tương ứng).
Vì $MK$ là đường cao nên $\widehat {MKN} = 90^\circ $;Vì $AH$ là đường cao nên $\widehat {AHB} = 90^\circ $
Xét $\Delta MNK$ và $\Delta ABH$ có:
$\widehat B = \widehat N$ (chứng minh trên)
$\widehat {MKN} = \widehat {AHB} = 90^\circ $
Do đó, $\Delta MNK\backsim\Delta ABH$ (g.g)
Vì $\Delta MNK\backsim\Delta ABH$ nên ta có: $\frac{{MN}}{{AB}} = \frac{{NK}}{{BH}} = \frac{{MK}}{{AH}} = k \Rightarrow \frac{{MK}}{{AH}} = k$.
b) Vì $\Delta MNP\backsim\Delta ABC$ nên $\frac{{MN}}{{AB}} = \frac{{NP}}{{BC}} = \frac{{MP}}{{AC}} = k$
$ \Rightarrow \frac{{NP}}{{BC}} = k \Leftrightarrow NP = kBC$
Vì $\frac{{MK}}{{AH}} = k \Rightarrow MK = kAH$
Diện tích tam giác $MNP$ là:
${S_1} = \frac{1}{2}.MK.NP$ (đvdt)
Diện tích tam giác $ABC$ là:
${S_2} = \frac{1}{2}.AH.BC$ (đvdt)
Ta có: $\frac{{{S_1}}}{{{S_2}}} = \frac{{\frac{1}{2}.MK.NP}}{{\frac{1}{2}.AH.BC}} = \frac{{kAH.kBC}}{{AH.BC}} = {k^2}$ (điều phải chứng minh)
Bài 1 trang 75 toán 8 tập 2
Hãy tìm cặp tam giác vuông đồng dạng trong Hình 8.
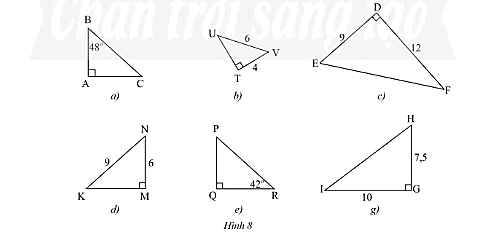
Hướng dẫn giải
Xét tam giác vuông $PQR$ có:
$\widehat P + \widehat Q + \widehat R = 180^\circ \Leftrightarrow \widehat P + 90^\circ + 42^\circ = 180^\circ \Rightarrow \widehat P = 180^\circ – 90^\circ – 42^\circ = 48^\circ $
Xét tam giác vuông $UVT$ có:
$U{V^2} = U{T^2} + V{T^2} \Leftrightarrow {6^2} = U{T^2} + {4^2} \Rightarrow U{T^2} = {6^2} – {4^2} = 20 \Rightarrow UT = 2\sqrt 5 $
Xét tam giác vuông $DEF$ có:
$E{F^2} = D{E^2} + D{F^2} \Leftrightarrow E{F^2} = {9^2} + {12^2} \Rightarrow E{F^2} = 225 \Rightarrow EF = 15$
Xét tam giác vuông $MNK$ có:
$K{N^2} = K{M^2} + M{N^2} \Leftrightarrow {9^2} = K{M^2} + {6^2} \Rightarrow K{M^2} = {9^2} – {6^2} = 45 \Rightarrow KM = 3\sqrt 5 $
Xét tam giác vuông $IGH$ có:
$I{H^2} = H{G^2} + I{G^2} \Leftrightarrow I{H^2} = 7,{5^2} + {10^2} \Rightarrow I{H^2} = 156,25 \Rightarrow IH = 12,5$
– Xét $\Delta ABC$ và $\Delta QPR$ có:
$\widehat B = \widehat P = 48^\circ $ (chứng minh trên)
$\widehat A = \widehat Q = 90^\circ $
Do đó, $\Delta ABC\backsim\Delta QPR$ (g.g)
– Xét $\Delta UTV$ và $\Delta KMN$ có:
$\widehat T = \widehat M = 90^\circ $
$\frac{{UT}}{{KM}} = \frac{{2\sqrt 5 }}{{3\sqrt 5 }} = \frac{2}{3};\frac{{VT}}{{MN}} = \frac{4}{6} = \frac{2}{3}$
Do đó, $\Delta UTV\backsim\Delta KMN$ (c.g.c)
– Xét $\Delta DEF$ và $\Delta GHI$ có:
$\widehat D = \widehat G = 90^\circ $
$\frac{{HG}}{{DE}} = \frac{{7,5}}{9} = \frac{5}{6};\frac{{IG}}{{DF}} = \frac{{10}}{{12}} = \frac{5}{6}$
Do đó, $\Delta DEF\backsim\Delta GHI$ (c.g.c).
Giải toán 8 tập 2 trang 76
Giải Bài 2 trang 76 toán 8 tập 2
Quan sát Hình 9.
a) Chứng minh rằng $\Delta DEF\backsim\Delta HDF$.
b) Chứng minh rằng $D{F^2} = FH.FE$.
c) Biết $EF = 15cm,FH = 5,4cm$. Tính độ dài đoạn thẳng $DF$.
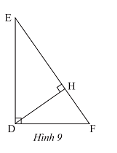
Hướng dẫn giải
a) Xét $\Delta DEF$ và $\Delta HDF$ có:
$\widehat F$ chung
$\widehat {EDF} = \widehat {DHF} = 90^\circ $
Do đó, $\Delta DEF\backsim\Delta HDF$ (g.g)
b) Vì $\Delta DEF\backsim\Delta HDF$ nên $\frac{{DF}}{{HF}} = \frac{{FE}}{{DF}}$ (các cặp cạnh tương ứng có cùng tỉ lệ)
$ \Rightarrow D{F^2} = FH.FE$.
c) Theo câu b ta có:
$D{F^2} = FH.FE$
Thay số, $D{F^2} = 5,4.15 = 81 \Rightarrow DF = \sqrt {81} = 9cm$
Vậy $DF = 9cm$.
Giải Bài 3 trang 76 toán 8 tập 2
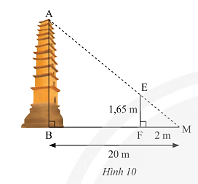
Trong Hình 10, biết $MB = 20m,MF = 2m,EF = 1,65m$. Tính chiều cao $AB$ của ngọn tháp.
Hướng dẫn giải
Xét $\Delta MEF$ và $\Delta MAB$ có:
$\widehat M$ chung
$\widehat {MFE} = \widehat {MBA} = 90^\circ $
Do đó, $\Delta MEF\backsim\Delta MAB$ (g.g)
Vì nên $\frac{{MF}}{{MB}} = \frac{{FE}}{{AB}}$ (các cặp cạnh tương ứng)
Thay số, $\frac{2}{{20}} = \frac{{1,65}}{{AB}} \Rightarrow AB = \frac{{1,65.20}}{2} = 16,5$
Vậy tòa tháp cao 16,5m.
Giải Bài 4 trang 76 toán 8 tập 2
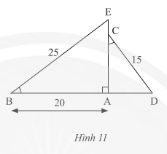
Trong Hình 11, cho biết $\widehat B = \widehat C,BE = 25cm,AB = 20cm,DC = 15cm$. Tính độ dài đoạn thẳng $CE$.
Hướng dẫn giải
Xét $\Delta ABE$ và $\Delta ACD$ có:
$\widehat {EBA} = \widehat {ACD}$ (giả thuyết)
$\widehat {BAE} = \widehat {CAD} = 90^\circ $
Do đó, $\Delta ABE\backsim\Delta ACD$ (g.g)
Vì $\Delta ABE\backsim\Delta ACD$ nên $\frac{{AB}}{{AC}} = \frac{{EB}}{{CD}}$ (các cặp cạnh tương ứng)
Thay số, $\frac{{20}}{{AC}} = \frac{{25}}{{15}} \Rightarrow AC = \frac{{20.15}}{{25}} = 12$cm.
Áp dụng định lí Py – ta – go cho $\Delta ABE$ vuông tại $A$ ta có:
$B{E^2} = A{E^2} + A{B^2} \\\Leftrightarrow A{E^2} = B{E^2} – A{B^2} = {25^2} – {20^2} = 225 \\\Rightarrow AE = \sqrt {225} = 15cm$
Độ dài $CE$ là:
15 – 12 = 3cm
Vậy $CE = 3cm.$
Giải Bài 5 trang 76 toán 8 tập 2
Quan sát Hình 12. Chứng minh rằng:

a) $\Delta ABH\backsim\Delta DCB$;
b) $\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}$.
Hướng dẫn giải
a) Vì $\left\{ \begin{array}{l}JC \bot AE\\BH \bot AE\end{array} \right. \Rightarrow JC//BH$. Vì $JC//BH \Rightarrow \widehat {HBA} = \widehat {JCA}$ (hai góc đồng vị)
hay $\widehat {HBA} = \widehat {DCB}$
Xét $\Delta ABH$ và $\Delta DCB$ có:
$\widehat {HBA} = \widehat {DCB}$ (chứng minh trên)
$\widehat {AHB} = \widehat {DBC} = 90^\circ $
Do đó, $\Delta ABH\backsim\Delta DCB$ (g.g)
b) Vì (hai góc tương ứng) hay $\widehat {EAB} = \widehat {CDB}$.
Xét $\Delta AEB$ và $\Delta DCB$ có:
$\widehat {EAB} = \widehat {CDB}$ (chứng minh trên)
$\widehat {ABE} = \widehat {DBC} = 90^\circ $
Do đó, $\Delta AEB\backsim\Delta DCB$ (g.g)
Suy ra, $\frac{{BE}}{{BC}} = \frac{{BA}}{{BD}}$ (các cặp cạnh tương ứng có cùng tỉ lệ)
Hay $\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}$ (điều phải chứng minh).
Giải Bài 6 trang 76 toán 8 tập 2
Một người đo chiều cao của một tòa nhà nhờ một cọc chôn xuống đất, cọc cao 3m và đặt cách xa tòa nhà 27m. Sau khi người ấy lùi xa cái cọc 1,2m thì nhìn thấy đầu cọc và đỉnh tòa nhà cùng năm trên một đường thẳng. Hỏi tòa nhà cao bao nhiêu mét, biết rằng khoảng cách từ chân đến mắt người ấy là 1,5m.
Hướng dẫn giải
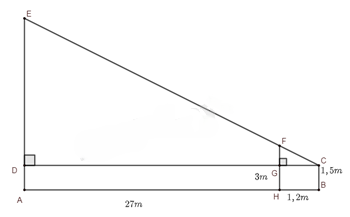
Giả sử, ta biểu diễn người quan sát, cái cọc, tòa nhà có dạng như hình vẽ.
Chiều cao người quan sát là $CB = 1,5m$; chiều cao cái cọc là $HF = 3m$; khoảng cách từ người đến cọc là $HB = 1,2m$; khoảng cách từ tòa nhà đến cọc là $AH = 27m$. Chiều cao tòa nhà là $AE$.
Vì tứ giác $GHBC$ là hình chữ nhật nên $GC = HB = 1,2m$; Vì tứ giác $GHAD$ là hình chữ nhật nên $AH = DG = 27m;GH = AD = 1,5m$.
Chiều dài đoạn $CD$ là: $DC = DG + GC = 27 + 1,2 = 28,2m$.
Độ dài đoạn $GF$ là: $GF = FH – GH = 3 – 1,5 = 1,5m$
Xét $\Delta DEC$ và $\Delta GFC$ có:
$\widehat C$ chung
$\widehat {EDC} = \widehat {FGC} = 90^\circ $
Do đó, $\Delta DEC\backsim\Delta GFC$ (g.g)
Vì $\Delta DEC\backsim\Delta GFC$ nên $\frac{{DC}}{{GC}} = \frac{{DE}}{{GF}}$ (các cặp cạnh tương ứng)
Thay số, $\frac{{28,2}}{{1,2}} = \frac{{DE}}{{1,5}} \Rightarrow DE = \frac{{28,2.1,5}}{{1,2}} = 35,25m$
Chiều cao của tòa nhà là:
$AD + DE = 35,25 + 1,5 = 36,75m$
Vậy chiều cao tòa nhà là 36,75m.
Giải Bài 7 trang 76 toán 8 tập 2
Cho tam giác $ABC$ vuông tại $A$ có đường cao $AH$. Kẻ $HM$ vuông góc với $AB$ tại $M$.
a) Chứng minh rằng $\Delta AMH\backsim\Delta AHB$.
b) Kẻ $HN$ vuông góc với $AC$ tại $N$. Chứng minh rằng $AM.AB = AN.AC$.
c) Chứng minh rằng $\Delta ANM\backsim\Delta ABC$.
d) Cho biết $AB = 9cm,AC = 12cm.$ Tính diện tích tam giác $AMN$.
Hướng dẫn giải
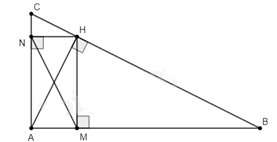
a) Xét $\Delta AMH$ và $\Delta AHB$ có:
$\widehat {HAM}$ chung (do $\widehat {HAM}$ cũng là $\widehat {HAB}$)
$\widehat {AMH} = \widehat {AHB} = 90^\circ $ (do $HM \bot AB$ và $AH$ là đường cao)
Do đó, $\Delta AMH\backsim\Delta AHB$ (g.g).
b) Vì $\Delta AMH\backsim\Delta AHB$ nên $\frac{{AM}}{{AH}} = \frac{{AH}}{{AB}}$ (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra $AM.AB = A{H^2}$ (1)
– Xét $\Delta ANH$ và $\Delta AHC$ có:
$\widehat {HAN}$ chung (do $\widehat {HAN}$ cũng là $\widehat {HAC}$)
$\widehat {ANH} = \widehat {AHC} = 90^\circ $ (do $HN \bot AC$ và $AH$ là đường cao)
Do đó, $\Delta ANH\backsim\Delta AHC$ (g.g).
Vì $\Delta ANH\backsim\Delta AHC$ nên $\frac{{AN}}{{AH}} = \frac{{AH}}{{AC}}$ (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra $AN.AC = A{H^2}$ (2)
Từ (1) và (2) suy ra, $AM.AB = AN.AC$(điều phải chứng minh).
c) Từ câu b ta có:
$AM.AB = AN.AC \Rightarrow \frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}$ (tỉ lệ thức)
Xét $\Delta ANM$và $\Delta ABC$ ta có:
$\widehat A$ chung
$\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}$ (chứng minh trên)
Do đó, $\Delta ANM\backsim\Delta ABC$(c.g.c)
d) Áp dụng định lí Py- ta – go cho tam giác $ABC$ vuông tại $A$ ta có:
$B{C^2} = A{B^2} + A{C^2} = {9^2} + {12^2} = 225 \Rightarrow BC = 15cm$
Diện tích tam giác $ABC$ là: ${S_{\Delta ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}AH.BC$
$ \Rightarrow AH.BC = AB.AC$
$ \Rightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{9.12}}{{15}} = 7,2cm$.
Ta có: $A{H^2} = AM.AB = AM.9 = 7,{2^2} \Rightarrow AM = \frac{{7,{2^2}}}{9} = 5,76cm$
$A{H^2} = AN.AC = AN.12 = 7,{2^2} \Rightarrow AN = \frac{{7,{2^2}}}{{12}}4,32cm$.
Diện tích tam giác vuông $AMN$ là:
${S_{AMN}} = \frac{1}{2}AM.AN = \frac{1}{2}.5,76.4,32 = 12,4416c{m^2}$.
Vậy diện tích tam giác $AMN$ là 12,4416cm2.
