Giải toán 8 tập 2 trang 90 Bài 1: Mô tả xác suất bằng tỉ số

Giải toán 8 tập 2 trang 90 bài 1 sách Chân trời sáng tạo có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 8 CTST. Mời các em học sinh cùng quý phụ huynh tham khảo.

Giải toán 8 tập 2 trang 88

Khởi động trang 88 Toán 8 tập 2

Đề bài

Một hộp có 1 quả bóng xanh và 4 quả bóng đỏ có kích thước và khối lượng như nhau. Châu lấy ra ngẫu nhiên 1 quả bóng từ hộp. Theo em, khả năng Châu lấy được bóng đỏ bằng mấy lần khả năng Châu lấy được bóng xanh?

Hướng dẫn giải

Ta dự đoán khả năng Châu lấy được bóng đỏ bằng 4 lần khả năng Châu lấy được bóng xanh vì bóng đỏ gấp 4 lần bóng xanh.

Hoạt động 1 trang 88 toán 8 tập 2

Một hộp chứa 10 tấm thẻ cùng loại được đánh số lần lượt từ 3 đến 12. Chọn ngẫu nhiên 1 tấm thẻ từ hộp. Hãy liệt kê các kết quả làm cho các biến cố sau xảy ra.

$A$:” Số ghi trên thẻ lấy ra chia hết cho 3”.

$B$:” Số ghi trên thẻ lấy ra chia hết cho 6”.

Hướng dẫn giải:

Khi lấy 1tấm thẻ ra khỏi hộp thì số chỉ trên tấm thẻ có thể là: thẻ 3; thẻ 4; thẻ 5; thẻ 6; thẻ 7; thẻ 8; thẻ 9; thẻ 10; thẻ 11; thẻ 12.

Các kết quả cho biến cố $A$: “ Số ghi trên thẻ lấy ra chia hết cho 3” là thẻ 3; thẻ 3; thẻ 9; thẻ 12.

Các kết quả cho biến cố $B$: “ Số ghi trên thẻ lấy ra chia hết cho 6” là thẻ 6; thẻ 12.

Thực hành 1 trang 88 toán 8 tập 2

Trên bàn có một tấm bìa hình tròn được chia thành 8 phần hình quạt bằng nhau và được đánh số từ 1 đến 8 như Hình 1. Xoay tấm bìa quanh tâm hình tròn và xem khi tấm bìa dừng lại, mũi tên chỉ vào ô ghi số nào. Xét các biến cố sau:

$A$: “Mũi tên chỉ vào ô ghi số chẵn”;

$B$: “Mũi tên chỉ vào ô ghi số chia hết cho 4”;

$C$: “Mũi tên chỉ vào ô ghi số nhỏ hơn 3”.

Hãy nêu các kết quả thuận lợi cho mỗi biến cố trên.

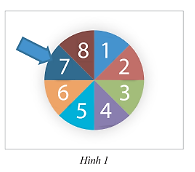
Hướng dẫn giải:

Khi quay tấm bìa, các kết quả có thể xảy ra là:

Mũi tên chỉ vào ô số 1; Mũi tên chỉ vào ô số 2; Mũi tên chỉ vào ô số 3; Mũi tên chỉ vào ô số 4; Mũi tên chỉ vào ô số 5; Mũi tên chỉ vào ô số 6; Mũi tên chỉ vào ô số 7; Mũi tên chỉ vào ô số 8.

– Các kết quả thuận lợi cho biến cố $A$ mũi tên chỉ vào ô số chẵn là ô số 2; ô số 4; ô số 6; ô số 8.

– Các kết quả thuận lợi cho biến cố $B$mũi tên chỉ vào ô số chia hết cho 4 là ô số 4; ô số 8.

– Các kết quả thuận lợi cho biến cố $C$ mũi tên chỉ vào ô số nhỏ hơn 3 là ô số 1; ô số 2.

Giải toán 8 tập 2 trang 89

Hoạt động 2 trang 89 toán 8 tập 2

Gieo một con xúc xắc cân đối đồng và đồng chất. Gọi $A$ là biến cố gieo được mặt có số chấm chia hết cho 3. Tính xác suất của biến cố $A$.

Hướng dẫn giải:

Số kết quả có thể xảy ra là 6 vì con xúc xắc có 6 mặt.

Số kết quả thuận lời của $A$ là 2 (ứng với mặt 3 chấm và mặt 6 châm).

Xác suất của biến cố $A$ là:

$P\left( A \right) = \frac{2}{6} = \frac{1}{3}$.

Thực hành 2 trang 89 toán 8 tập 2

Hãy trả lời câu hỏi ở trang (88)

Một hộp có 1 quả bóng xanh và 4 quả bóng đỏ có kích thước và khối lượng như nhau. Châu lấy ra ngẫu nhiên 1 quả bóng từ hộp. Theo em, khả năng Châu lấy được bóng đỏ bằng mấy lần khả năng Châu lấy được bóng xanh.?

Hướng dẫn giải:

Có tất cả 5 quả bóng nên số kết quả có thể xảy ra là 5.

Gọi $A$ là biến cố lấy được bóng màu đỏ và $B$ là biến cố lấy được bóng màu xanh.

Biến cố $A$ xảy ra khi lấy được bóng màu đỏ và ở đây có 4 quả bóng màu đỏ nên số kết quả thuận lợi là 4. Xác suất của biến cố $A$ là:

$P\left( A \right) = \frac{4}{5}$

Biến cố $B$ xảy ra khi lấy được bóng màu xanh và ở đây có 1 quả bóng màu xanh nên số kết quả thuận lợi là 1. Xác suất của biến cố $B$ là:

$P\left( B \right) = \frac{1}{5}$

Khả năng Châu lấy được bóng đỏ gấp số lần khả năng Châu lấy được bóng xanh là:

$\frac{4}{5}:\frac{1}{5} = \frac{4}{1} = 4$

Giải toán 8 tập 2 trang 90

Giải Vận dụng trang 90 toán 8 tập 2

Một khu phố có 200 người lao động, mỗi người làm việc ở trong năm lĩnh vực là Kinh doanh, Sản xuất, Giáo dục, Y tế và Dịch vụ. Biểu đồ trong Hình 2 thông kê tỉ lệ người lao động thuộc mỗi lĩnh vực nghề nghiệp.

Gặp ngẫu nhiên một người lao động của khu phố.

a) Tính xác suất người đó có công việc thuộc lĩnh vực Giáo dục.

b) Tính xác suất người đó có công việc không thuộc lĩnh vực Y tế hay Dịch vụ.

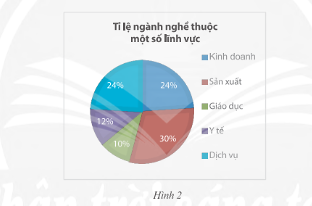
Hướng dẫn giải:

Vì gặp ngẫu nhiên một người trong 200 người nên 200 kết quả có khả năng xảy ra như nhau.

Số người làm Kinh doanh trong 200 người ở khu phố là:

$200.24\%  = 48$ (người)

Số người làm Y tế trong 200 người ở khu phố là:

$200.12\%  = 24$ (người)

Số người làm Giáo dục trong 200 người ở khu phố là:

$200.10\%  = 20$ (người)

Số người làm Sản xuất trong 200 người ở khu phố là:

$200.30\%  = 60$ (người)

Số người làm Dịch vụ trong 200 người ở khu phố là:

$200.24\%  = 48$ (người)

a) Gọi $A$ là biến cố người gặp ngẫu nhiên là người làm trong lĩnh vực giáo dục.

Biến cố $A$ xảy ra khi người gặp ngẫu nhiên là người làm trong lĩnh vực giáo dục do đó, số kết quả thuận lợi của biến cố $A$ là 20. Xác suất của biến cố $A$ là:

$P\left( A \right) = \frac{{20}}{{200}} = \frac{1}{{10}}$

b) Gọi $B$ là biến cố người gặp ngẫu nhiên không thuộc lĩnh vực Y tế hay Dịch vụ do đó, người gặp ngẫu nhiên có thể thuộc lĩnh vực Kinh doanh, Giáo dục hoặc Sản xuất.

Biến cố $B$ xảy ra khi người gặp ngẫu nhiên là người làm trong lĩnh vực Kinh doanh, Giáo dục hoặc Sản xuất do đó, số kết quả thuận lợi của biến cố $B$ là: 48 + 20 + 60 = 128.

Xác suất của biến cố $B$ là:

$P\left( B \right) = \frac{{128}}{{200}} = \frac{{16}}{{25}}$.

Giải Bài 1 trang 90 toán 8 tập 2

Trong hộp có 5 quả bóng có kích thước và khối lượng giống nhau và được đánh số lần lượt là 5; 8; 10; 13; 16. Lấy ngẫu nhiên 1 quả bóng từ hộp. Tính xác suất  của các biến cố:

$A$: “Số ghi trên quả bóng là số lẻ”.

$B$: “Số ghi trên quả bóng chia hết cho 3”.

$C$: “Số ghi trên quả bóng lớn hơn 4”.

Hướng dẫn giải

Vì 5 quả bóng có kích thước và khối lượng giống nhau nên 5 kết quả của phép thử có khả năng xảy ra bằng nhau.

– Biến cố $A$ xảy ra khi ta lấy được quả bóng có số 5 hoặc 13 nên có 2 kết quả thuận lợi cho $A$. Xác suất của biến có $A$ là:

$P\left( A \right) = \frac{2}{5}$.

– Vì không có quả bóng nào đánh số chia hết cho 3 nên số kết quả thuận lợi của biến cố $B$ là 0. Xác suất của biến cố $B$ là

$P\left( B \right) = \frac{0}{5} = 0$.

– Vì cả 5 quả bóng đều đánh số lớn hơn 4 nên số kết quả thuận lợi của biến cố $C$ là 5. Xác suất của biến cố $C$ là

$P\left( C \right) = \frac{5}{5} = 1$.

Giải Bài 2 trang 90 toán 8 tập 2

Một hộp chứ 3 viên bi xanh, 4 viên bi đỏ và 5 viên bi vàng có kích thước và khối lượng giống nhau. Lấy ra ngẫu nhiên 1 viên bi từ hộp. Tính xác suất của các biến cố:

$A$: “Viên bi lấy ra có màu xanh”.

$B$: “Viên bi lấy ra không có màu đỏ”.

Hướng dẫn giải

Vì 3 viên bi xanh, 4 viên bi đỏ và 5 viên b vàng có kích thước và khối lượng như nhau nên 12 kết quả của phép thử có khả năng xảy ra bằng nhau.

– Biến cố $A$ xảy ra khi ta lấy được viên bi màu xanh nên có 3 kết quả thuận lợi cho $A$. Xác suất của biến có $A$ là:

$P\left( A \right) = \frac{3}{{12}} = \frac{1}{4}$.

– Biến cố $B$ xảy ra khi ta lấy được viên bi không có màu đỏ nên viên bi lấy được có thể có màu xanh hoặc màu vàng. Do đó, có 8 kết quả thuận lợi cho $B$. Xác suất của biến có $B$ là:

$P\left( B \right) = \frac{8}{{12}} = \frac  {2}{3}$.

Giải toán 8 tập 2 trang 91

Bài 3 trang 91 toán 8 tập 2

Trong hộp có 10 tấm thẻ cùng loại, trên mỗi tấm thẻ có ghi một số tự nhiên. Lấy ra ngẫu nhiên 1 thẻ từ hộp. Biết rằng xác suất lấy được thẻ ghi số chẵn gấp 4 lần xác suất lấy được thẻ ghi số lẻ. Hỏi trong hộp có bao nhiêu thẻ ghi số lẻ?

Hướng dẫn giải

Gọi số thẻ ghi số lẻ trong hộp là $n$. Khi đó, xác suất tấm thẻ lấy ra ghi số lẻ là $\frac{n}{{10}}$.

Số thẻ ghi số chẵn trong hộp là $10 – n$. Khi đó, xác suất tấm thẻ lấy ra ghi số chẵn là $\frac{{10 – n}}{{10}}$.

Vì xác suất lấy được thẻ chẵn gấp 4 lần xác suất lấy được thẻ lẻ nên $\frac{{10 – n}}{{10}} = 4.\frac{n}{{10}} \Leftrightarrow 10 – n = 4n \Leftrightarrow 5n = 10 \Leftrightarrow n = 2$

Vậy số thẻ ghi số lẻ trong hộp là 2 thẻ.

Bài 4 trang 91 toán 8 tập 2

Số lượng học sinh tham gia Câu lạc bộ Cờ vua của một trường được biểu diễn ở biểu đồ sau:

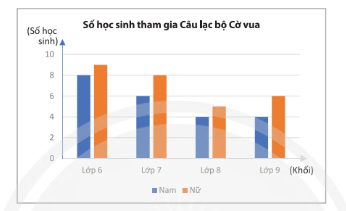
Chọn ngẫu nhiên 1 học sinh trong Câu lạc bộ Cờ vua của trường đó. Tính xác suất các biến cố:

$A$: “Học sinh được chọn là nữ”.

$B$: “Học sinh được chọn học lớp 8”.

$C$: “Học sinh được chọn là nam và không học lớp 7”.

Hướng dẫn giải

Tổng số học sinh tham gia câu lạc bộ là:

$8 + 9 + 6 + 8 + 4 + 5 + 4 + 6 = 50$ (học sinh)

– Biến cố $A$ xảy ra khi bạn học sinh chọn được là nữ.

Số học sinh nữ tham gia câu lạc bộ là:

$9 + 8 + 5 + 6 = 28$ (học sinh)

Xác suất của biến có $A$ là:

$P\left( A \right) = \frac{{28}}{{50}} = \frac{{14}}{{25}}$

– Biến cố $B$ xảy ra khi bạn học sinh chọn được là học sinh lớp 8.

Số học sinh lớp 8 trong câu lạc bộ là:

$4 + 5 = 9$(học sinh)

Xác suất của biến có $B$ là:

$P\left( B \right) = \frac{9}{{50}}$

– Biến cố $C$ xảy ra khi bạn học sinh chọn được là nam và không học lớp 7.

Số học sinh câu lạc bộ là nam và không học lớp 7 là:

$8 + 4 + 4 = 16$

Xác suất của biến có $C$ là:

$P\left( C \right) = \frac{{16}}{{50}} = \frac{8}{{25}}$

Bài 5 trang 91 toán 8 tập 2

Một trường trung học có sở có 600 học sinh. Tỉ lệ phần trăm học sinh mỗi khối được cho bởi biểu đồ trong Hình 4. Chọn ngẫu nhiên một học sinh trong trường để dự phỏng vấn. Biết rằng mọi học sinh của trường đều có khả năng được lựa chọn như nhau.

a) Tính xác suất của biến cố “Học sinh được chọn thuộc khối 9”.

b) Tính xác suất của biến cố “Học sinh được chọn không thuộc khối 6”.

Hướng dẫn giải

Số học sinh khối 6 là:

$600.28\%  = 168$ (học sinh)

Số học sinh khối 7 là:

$600.22\%  = 132$ (học sinh)

Số học sinh khối 8 là:

$600.26\%  = 156$ (học sinh)

Số học sinh khối 6 là:

$600.24\%  = 144$ (học sinh)

a) Gọi $A$ là biến cố: “Học sinh được chọn thuộc khối 9”.

Biến cố $A$ xảy ra khi bạn học sinh chọn được là học sinh khối 9.

Xác suất của biến có $A$ là:

$P\left( A \right) = \frac{{144}}{{600}} = \frac{6}{{25}}$

b) Gọi $B$ là biến cố: “Học sinh được chọn không thuộc khối 6”.

Biến cố $B$ xảy ra khi bạn học sinh chọn được là học sinh khối 7, khối 8, khối 9.

Tổng số học sinh khối 7, khối 8 và khối 9 là:

$132 + 156 + 144 = 432$ (học sinh)

Xác suất của biến có $B$ là:

$P\left( B \right) = \frac{{432}}{{600}} = \frac{{72}}{{100}}$.