Bài 1: Tỉ số lượng giác của góc nhọn Toán lớp 9 tập 1

Giải Bài 1: Tỉ số lượng giác của góc nhọn Toán lớp 9 tập 1 có đáp án chi tiết cho từng bài tập trong sách giáo khoa toán lớp 9 tập 1 Chân trời sáng tạo. Mời các em học sinh cùng quý phụ huynh tham khảo.

Giải Toán 9 trang 63

Thực hành 3 trang 63 Toán 9 Tập 1:

a) So sánh: sin 72° và cos 18°; cos 72° và sin 18°; tan 72° và cot 18°.

b) Cho biết sin 18° ≈ 0,31; tan 18° ≈ 0,32. Tính cos 72° và cot 72°.

Lời giải

a) sin 72° = cos (90° – 72°) = cos 18°;

cos 72° = sin(90° – 72°) = sin 18°;

tan 72° = cot(90° – 72°) = cot 18°.

Vậy sin 72° = cos 18°; cos 72° = sin 18°; tan 72° = cot 18°.

b) Theo đề bài ta có: sin 18° ≈ 0,31; tan 18° ≈ 0,32.

Suy ra cos 72° = sin(90° – 72°) = sin 18° ≈ 0,31.

và cot 72° = tan(90° – 72°) = tan 18° ≈ 0,32.

Vậy cos 72° ≈ 0,31 và cot 72° ≈ 0,32.

Vận dụng 3 trang 63 Toán 9 Tập 1:

Tia nắng chiếu qua điểm B của nóc tòa nhà tạo với mặt đất một góc x và tạo với cạnh AB của tòa nhà một góc y (Hình 9). Cho biết cos x ≈ 0,78 và cot x ≈ 1,25. Tính sin y và tan y (kết quả làm tròn đến hàng phần trăm).

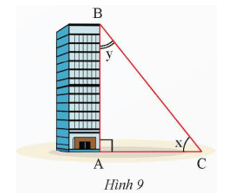
Lời giải

Xét tam giác ABC vuông tại A, áp dụng tỉ số lượng giác hai góc phụ nhau, ta có:

sin y = cos x ≈ 0,78; tan y = cot x ≈ 1,25.

Vậy sin y ≈ 0,78 và tan y ≈ 1,25.

Giải Toán 9 trang 65

Thực hành 4 trang 65 Toán 9 Tập 1:

a) Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau (kết quả làm tròn đến hàng phần nghìn):

22°; 52°; 15°20′; 52°18′.

b) Tìm các góc nhọn x, y, z, t trong mỗi trường hợp sau (kết quả làm tròn đến hàng phần trăm hoặc đến phút):

sin x = 0,723; cos y = 0,828;

tan z = 3,77; cot t = 1,54.

Lời giải

a) Sử dụng máy tính cầm tay, ta tính được:

• Các tỉ số lượng giác của các góc 22° là:

sin 22° ≈ 0,375; cos 22° ≈ 0,927;

tan 22° ≈ 0,404; cot 22° ≈ 2,475.

• Các tỉ số lượng giác của các góc 52° là:

sin 52° ≈ 0,788; cos 52° ≈ 0,616;

tan 52° ≈ 1,280; cot 52° ≈ 0,781.

• Các tỉ số lượng giác của các góc 15°20′ là:

sin 15°20′ ≈ 0,264; cos 15°20′ ≈ 0,964;

tan 15°20′ ≈ 0,274; cot 15°20′ ≈ 3,647.

• Các tỉ số lượng giác của các góc 52°18′ là:

sin 52°18′ ≈ 0,791; cos 52°18′ ≈ 0,6115;

tan 52°18′ ≈ 1,294; cot 52°18′ ≈ 0,773.

b) Sử dụng máy tính cầm tay, ta có:

• sin x = 0,723 nên x ≈ 46°18′.

• cos y = 0,828 nên y ≈ 34°6′.

• tan z = 3,77 nên z ≈ 75°8′.

• cot t = 1,54 nên t ≈ 32°59′.

Vận dụng 4 trang 65 Toán 9 Tập 1:

a) Vẽ một tam giác vuông có một góc bằng 40°. Đo độ dài các cạnh rồi dùng các số đo để tính các tỉ số lượng giác của góc 40°. Kiểm tra lại các kết quả vừa tính bằng máy tính cầm tay.

b) Vẽ một tam giác vuông có ba cạnh bằng 3 cm, 4 cm, 5 cm. Tính các tỉ số lượng giác của mỗi góc nhọn. Dùng thước đo góc để đo các góc nhọn. Kiểm tra lại các kết quả bằng máy tính cầm tay.

Lời giải

a) Vẽ tam giác vuông có một góc bằng 40°.

• Chẳng hạn tam giác ABC vuông tại A có \(\hat{B}\)=40° .

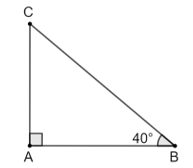
• Ta đo độ dài các cạnh của tam giác ABC lần lượt là:

AB = 5 cm, AC = 4 cm và BC ≈ 6,4 cm.

• Từ các độ dài các cạnh đo được, ta có các tỉ số lượng giác của góc 40° như sau:

• Kiểm tra lại bằng máy tính, ta có:

sin 40° ≈ 0,64; cos 40° ≈ 0,77;

tan 40° ≈ 0,84; cot 40° ≈ 1,19.

Nhận xét: Tỉ số lượng giá sau khi vẽ hình, đo độ dài các cạnh và tính so với tính bằng máy tính cầm tay, ta thu được hai kết quả gần bằng nhau.

b) Vẽ một tam giác vuông có ba cạnh bằng 3 cm, 4 cm, 5 cm.

• Chẳng hạn tam giác MNP vuông có MP = 3 cm, MN = 4 cm, NP = 5 cm.

Ta có MP² + MN² = 3² + 4² = 5² = NP².

Theo định lí Pythagore, ta có tam giác MNP vuông tại M.

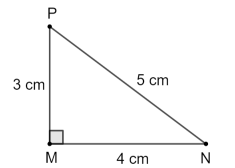
• Các tỉ số lượng giác của góc N là:

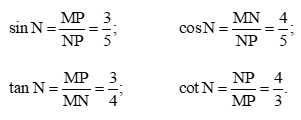
• Vì tam giác MNP vuông tại M nên \(\hat{N}\) và \(\hat{P}\) là hai góc phụ nhau.

Khi đó, các tỉ số lượng giác của góc P là:

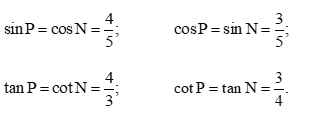
Dùng thước đo góc, ta có: \(\hat{P}\) ≈ 53,1° ;\(\hat{N}\) ≈ 36,9°

Từ các tỉ số lượng giác ở trên, sử dụng máy tính cầm tay, ta thu được kết quả xấp xỉ kết quả khi đo góc.

Giải Toán 9 trang 66

Bài 1 trang 66 Toán 9 Tập 1:

Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác của góc B trong mỗi trường hợp sau:

a) BC = 5 cm; AB = 3 cm;

b) BC = 13 cm; AC = 12 cm;

c) BC=\(5\sqrt{2}\)cm; AB=5 cm;

d) AB=\(a\sqrt{3}\) ; AC=a.

Bài 2 trang 66 Toán 9 Tập 1:

Tính giá trị của các biểu thức sau:

a) \(A = \frac{{\sin {{30}^o}.\cos {{30}^o}}}{{\cot {{45}^o}}}\)

b) \(B = \frac{{\tan {{30}^o}}}{{\cos {{45}^o}.\cos {{60}^o}}}\)

Lời giải chi tiết

a) \(A = \frac{{\sin {{30}^o}.\cos {{30}^o}}}{{\cot {{45}^o}}} = \frac{{\frac{1}{2}.\frac{{\sqrt 3 }}{2}}}{1} = \frac{{\sqrt 3 }}{4} \approx 0,43\)

b) \(B = \frac{{\tan {{30}^o}}}{{\cos {{45}^o}.\cos {{60}^o}}} = \frac{{\frac{{\sqrt 3 }}{3}}}{{\frac{{\sqrt 2 }}{2}.\frac{1}{2}}} = \frac{{2\sqrt 6 }}{3} \approx 1,63\)

Bài 3 trang 66 Toán 9 Tập 1:

Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45°:

a) sin 60°;

b) cos 75°;

c) tan 80°.

Lời giải

a) sin 60° = cos (90° – 60°) = cos 30°;

b) cos 75° = sin (90° – 75°) = cos 15°;

c) tan 80° = cot (90° – 80°) = cot 10°.

Bài 4 trang 66 Toán 9 Tập 1:

Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau:

a) 26°;

b) 72°;

c) 81°27′.

Lời giải

Sử dụng máy tính cầm tay, ta tính được các tỉ số lượng giác như sau:

a) Tỉ số lượng giác của góc 26° là:

sin 26° ≈ 0,44; cos 26° ≈ 0,9;

tan 26° ≈ 0,49; cot 26° ≈ 2,05.

b) Tỉ số lượng giác của góc 72° là:

sin 72° ≈ 0,95; cos 72° ≈ 0,31;

tan 72° ≈ 3,08; cot 72° ≈ 0,32.

c) Tỉ số lượng giác của góc 81°27′ là:

sin 81°27′ ≈ 0,99; cos 81°27′ ≈ 0,15;

tan 81°27′ ≈ 6,65; cot 81°27′ ≈ 0,15.

Bài 5 trang 66 Toán 9 Tập 1:

Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau:

a) cos α = 0,6;

b) tanα=34.

Lời giải

a) Để tìm α khi biết cos α = 0,6, ta ấn liên tiếp các nút sau đây:

Và được kết quả như hình dưới đây:

Làm tròn đến hàng phần trăm, ta được α ≈ 53,13°.

Khi ta ấn thêm nút  thì được kết quả như hình dưới đây:

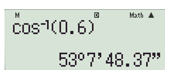
Làm tròn đến hàng phần trăm, ta được α ≈ 53°7′.

Vậy α ≈ 53,13° hoặc α ≈ 53°7′.

b) tan𝛼=\(\frac{3}{4}\)nên α ≈ 36°52′.

Để tìm α khi biết tan𝛼=\(\frac{3}{4}\), ta ấn liên tiếp các nút sau đây:

Và được kết quả như hình dưới đây:

Làm tròn đến hàng phần trăm, ta được α ≈ 36,87°.

Khi ta ấn thêm nút  thì được kết quả như hình dưới đây:

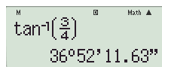
Làm tròn đến hàng phần trăm, ta được α ≈ 36°52′.

Vậy α ≈ 36,87° hoặc α ≈ 36°52′.

Bài 6 trang 66 Toán 9 Tập 1:

Tia nắng chiếu qua nóc của một tòa nhà hợp với mặt đất một góc α. Cho biết tòa nhà cao 21 m và bóng của nó trên mặt đất dài 15 m (Hình 10). Tính góc α (kết quả làm tròn đến độ).

Lời giải chi tiết

Theo đề bài ta có tam giác vuông sau:

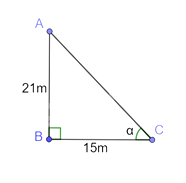
Ta có tan \(\alpha = \frac{{AB}}{{AC}} = \frac{{21}}{{15}} = \frac{7}{5}\)

Sử dụng máy tính cầm tay, ta được góc \(\alpha  \approx {54^o}\).

Bài 7 trang 66 Toán 9 Tập 1:

Một cái thang 12 m được đặt vào một bức tường sao cho chân thang cách tường 7 m (Hình 11). Tính góc α tạo bởi thang và tường.

Lời giải

Gọi giao điểm giữa bức tường và mặt đất là C.

Bức tường vuông góc với mặt đất nên AC ⊥ BC hay ACB^=90°.

Xét tam giác ABC vuông tại C, ta có: sinα=\(\frac{AC}{AB} =\frac{7}{12}\)

Sử dụng máy tính cầm tay, ta được α ≈ 36° (làm tròn đến độ).