Bài 35: Góc ở tâm, góc nội tiếp Toán lớp 9 tập 1

Giải Bài 35: Góc ở tâm, góc nội tiếp Toán lớp 9 tập 1 có đáp án chi tiết cho từng bài tập trong sách giáo khoa toán lớp 9 tập 1 Chân trời sáng tạo. Mời các em học sinh cùng quý phụ huynh tham khảo.

Giải Toán 9 trang 90

Khám phá 1 trang 90 Toán 9 Tập 1

Cho hai điểm A, B trên đường tròn (O; R). Nêu nhận xét về đỉnh và cạnh của \(\widehat {AOB}\).

Lời giải

Xét \(\widehat {AOB}\), có:

⦁ Đỉnh là O, trùng với tâm của đường tròn (O; R);

⦁ Hai cạnh là OA, OB là bán kính của đường tròn (O; R).

Thực hành 1 trang 90 Toán 9 Tập 1

Tính số đo góc ở tâm \(\widehat {EOA}\) và \(\widehat {AOB}\) trong Hình 3. Biết AC và BE là hai đường kính của đường tròn (O).

Lời giải

Xét đường tròn (O):

⦁ \(\widehat {EOA}\)=\(\widehat {BOC}\)=57° (đối đỉnh);

⦁\(\widehat {AOB}\)=\(\widehat {COE}\)=\(\widehat {COD}\) + \(\widehat {DOE}\)= 95°+28°=123°.

Giải Toán 9 trang 91

Vận dụng 1 trang 91 Toán 9 Tập 1

Tính số đo góc ở tâm được tạo thành khi kim giờ quay:

a) Từ 7 giờ đến 9 giờ;

b) Từ 9 giờ đến 12 giờ.

Lời giải

Sau 12 giờ, kim giờ sẽ quay được một vòng, ứng với 360°.

Mỗi giờ kim giờ quay được một góc ở tâm có số đo là \(\frac{360°}{12}\)=30°.

a) Từ 7 giờ đến 9 giờ, kim giờ quay một góc ở tâm có số đo là: (9−7)⋅30°=60°.

b) Từ 9 giờ đến 12 giờ, kim giờ quay một góc ở tâm có số đo là: (12−9)⋅30°=90°.

Khám phá 2 trang 91 Toán 9 Tập 1

Vẽ vào vở đường tròn (O) và hai điểm A, B nằm trên (O). Dùng bút chì khác màu tô hai phần của đường tròn được phân chia bởi hai điểm A và B.

Lời giải

Khám phá 3 trang 91 Toán 9 Tập 1

Cho OA và OB là hai bán kính vuông góc với nhau của đường tròn (O), C là điểm trên cung nhỏ AB (Hình 7). Ta coi số đo của một cung nhỏ là số đo của góc ở tâm chắn cung đó.

a) Xác định số đo của cung AB.

b) So sánh số đo của hai cung AC⏜ và AB⏜.

Lời giải

a) Số đo của cung AB là số đo của \(\widehat {AOB}\) và bằng 90°.

b) Ta có số đo của cung AC là số đo của \(\widehat {AOC}\)

Mà \(\widehat {AOC}\)<\(\widehat {AOB}\) nên số đo của cung AC nhỏ hơn số đo của cung AB.

Bài 1 trang 97 Toán 9 Tập 1

Cho đường tròn (O; 5 cm) và điểm M sao cho OM = 10 cm. Qua M vẽ hai tiếp tuyến với đường tròn tại A và B. Tính số đo góc ở tâm được tạo bởi hai tia OA và OB.

Lời giải

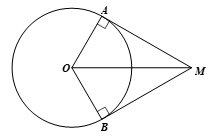
Ta có MA, MB là hai tiếp tuyến tại A và B nên MA \bot OA và MB \bot OB

Xét tam giác MAO vuông tại A, ta có:

\({\rm{cos}}\widehat {MOA} = \frac{{AO}}{{MO}} = \frac{5}{{10}} = \frac{1}{2}\)

Suy ra \(\widehat {MOA}\)= 60^o

Ta có hai tam giác vuông bằng nhau là: \(\Delta MAO = \Delta MBO\) (cạnh huyền- cạnh góc vuông).

Suy ra \(\widehat {MOA} = \widehat {MOB}\)= 60^o

Mà góc ở tâm được tạo bởi hai tia OA và OB là

\(\widehat {AOB} = \widehat {MOA} + \widehat {MOB} = {60^o}.2 = {120^o}\)

Bài 2 trang 97 Toán 9 Tập 1

Cho tam giác đều ABC. Vẽ nửa đường tròn đường kính BC cắt cạnh AB và AC lần lượt tại D và E. Hãy so sánh các cung \(\overset\frown{BD};\overset\frown{BE};\overset\frown{EC}.\)

Lời giải

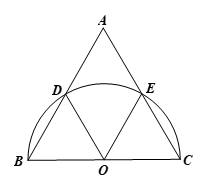
Gọi O là tâm đường tròn đường kính BC.

Ta có OB = OD (= R)

Vậy tam giác BOD cân tại O

Mà \(\widehat {DBO}\)= 60^o nên tam giác BOD đều

Suy ra \(\widehat {DOB}\)= 60^o

OE = DC (= R)

Vậy tam giác EOC cân tại O

Mà\(\widehat {ECO}\)= 60^o nên tam giác EOC đều

Suy ra \(\widehat {EOC}\)= 60^o

Ta có \(\widehat {BOD} + \widehat {DOE} + \widehat {EOC} = {180^o}\)

Suy ra 60^o +\(\widehat {DOE} + {60^o} = {180^o}\) nên \(\widehat {DOE} = {60^o}\)

Vì \(\widehat {BOD} = \widehat {DOE} = \widehat {EOC} = {60^o}\) nên \(sđ\overset\frown{BD} = sđ\overset\frown{BE} = sđ\overset\frown{EC}={{60}^{o}}\)

Vậy \(\overset\frown{BD}=\overset\frown{BE}=\overset\frown{EC}\)

Bài 3 trang 97 Toán 9 Tập 1

Dây cung AB chia đường tròn (O) thành hai cung. Cung lớn có số đo bằng ba lần cung nhỏ.

a) Tính số đo mỗi cung.

b) Chứng minh khoảng cách OH từ tâm O đến dây cung AB có độ dài bằng \(\frac{AB}{2}\)

Lời giải chi tiết

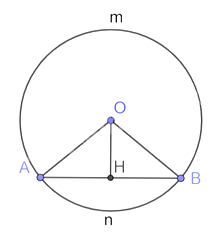
a) Gọi \(\overset\frown{AnB}\) là cung nhỏ và \(\overset\frown{AmB}\) là cung lớn có sđ\(\overset\frown{AmB}\) = 3sđ\(\overset\frown{AnB}\) (gt)

Mà sđ\(\overset\frown{AmB}\) + sđ\(\overset\frown{AnB}\) = 360^o

Do đó 4sđ\(\overset\frown{AnB}\) = 360^o

sđ\(\overset\frown{AnB}\) = 360^o: 4 = 90^o

Vậy sđ\(\overset\frown{AmB}\) = 3sđ\(\overset\frown{AnB}\) = 3. 90^o = 270^o .

b) Ta có \(\widehat {AOB}\)= sđ\(\overset\frown{AnB}\) (góc ở tâm chắn cung AB)

suy ra \(\widehat {AOB}\)= 90^o suy ra tam giác AOB vuông tại O.

Mà AO = OB = R nên tam giác AOB vuông cân tại O.

Khi đó OH là đường cao đồng thời là đường trung tuyến.

Tam giác AOB vuông tại O có OH là đường trung tuyến ứng với cạnh huyền nên OH = \(\frac{{AB}}{2}\).

Bài 4 trang 97 Toán 9 Tập 1

Kim giờ và kim phút của đồng hồ tạo thành một góc ở tâm có số đo là bao nhiêu vào những thời điểm sau?

a) 2 giờ;

b) 8 giờ;

c) 21 giờ.

Lời giải

Góc ở tâm tạo bởi hai kim giữa hai số liền nhau là: 360° : 12 = 30°.

a) Vào thời điểm 2 giờ (kim giờ chỉ số 2, kim phút chỉ số 12) thì góc ở tâm tạo thành giữa hai kim đồng hồ là:

2 . 30° = 60°.

b) Vào thời điểm 8 giờ (kim giờ chỉ số 8, kim phút chỉ số 12) thì góc ở tâm tạo thành giữa hai kim đồng hồ là:

4 . 30° = 120°.

c) Vào thời điểm 21 giờ (kim giờ chỉ số 9, kim phút chỉ số 12) thì góc ở tâm tạo thành giữa hai kim đồng hồ là:

3 . 30° = 90°.

Bài 5 trang 97 Toán 9 Tập 1

Cho hai đường tròn đồng tâm (O; R) và (O;\(\frac{{R\sqrt 3 }}{2}\)). Một tiếp tuyến của đường tròn nhỏ cắt đường tròn lớn tại hai điểm A và B. Tính số đo cung AB.

Lời giải

Gọi H là tiếp điểm của tiếp tuyến của đường tròn đã cho.

Xét tam giác OHB vuông tại H, ta có:

\(cos\widehat {HOB}= \frac{{OH}}{{OB}} = \frac{{\frac{{R\sqrt 3 }}{2}}}{R} = \frac{{\sqrt 3 }}{2}\)

suy ra \(\widehat {HOB}\) = 30^o

Ta có OA = OB (= R) nên tam giác OAB cân tại O

Mà OH là đường cao của tam giác AOB

Nên OH cũng là đường phân giác của tam giác AOB

Suy ra \(\widehat {AOB} = 2\widehat {HOB} = {2.30^o} = {60^o}\)

Do đó \(sđ\overset\frown{AB} =\widehat {AOB} = {60^o}.\)

Bài 6 trang 97 Toán 9 Tập 1

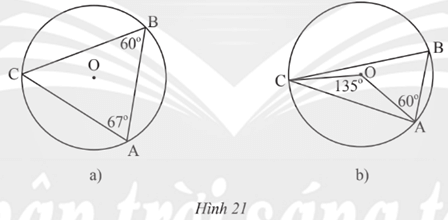
Xác định số đo các cung \(\overset\frown{AB};\overset\frown{BC};\overset\frown{CA}\) trong mỗi hình vẽ sau:

Lời giải chi tiết

a) Xét tam giác ABC, ta có: \(\widehat{ACB}={{180}^{o}}-\widehat{CBA}-\widehat{BAC}={{180}^{o}}-{{60}^{o}}-{{67}^{o}}={{53}^{o}}\)

Ta có sđ\(\overset\frown{AB}\) = 2.\(\widehat{ACB}\) = 2. 53^o = 106^o (Vì \(\widehat{ACB}\) là góc nội tiếp chắn cung AB)

Ta có sđ\(\overset\frown{BC}\) = 2.\(\widehat{BAC}\) = 2. 67^o = 134^o (Vì \(\widehat{BAC}\) là góc nội tiếp chắn cung BC)

Ta có sđ\(\overset\frown{AC}\) = 2.\(\widehat{ABC}\) = 2. 60^o = 120^o (Vì \(\widehat{ABC}\) là góc nội tiếp chắn cung AC).

b) Ta có sđ\(\overset\frown{AC}\) và góc ở tâm \(\widehat{COA}\) cùng chắn cung AC

suy ra sđ\(\overset\frown{AC}\) = \(\widehat{COA}\) = 135^o.

Nối O với B.

Xét tam giác OAB có AO = OB (= R) suy ra tam giác OAB cân tại A.

Mặt khác, \(\widehat {OAB} = {60^o}\) nên tam giác OAB là tam giác đều.

Ta có sđ\(\overset\frown{AB}\) = \(\widehat{AOB}\) = \({{60}^{o}}\) (Vì \(\widehat{AOB}\) là góc nội tiếp chắn cung AB)

Suy ra sđ\(\overset\frown{BC}\) = 360^o – sđ\(\overset\frown{AB}\) – sđ\(\overset\frown{AC}\) = 360^o – \({60^o}\) – 135^o = 165^o.

Bài 7 trang 97 Toán 9 Tập 1

Cho đường tròn (O) có hai đường kính AB, CD vuông góc với nhau. Lấy một điểm M trên cung nhỏ AC rồi vẽ tiếp tuyến với đường tròn (O) tại M. Tiếp tuyến này cắt đường thẳng CD tại S. Chứng minh rằng \(\widehat {MSD} = 2\widehat {MBA}.\)

Lời giải

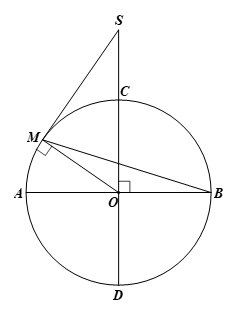
Ta có \(SM \bot OM\) (Tính chất tiếp tuyến)

Suy ra tam giác OSM vuông tại M

Ta có \(\widehat {MSO} + \widehat {MOS} = {90^o}\)

Và \(AB \bot CD\) (gt)

Suy ra \(\widehat {MOS} + \widehat {MOA} = {90^o}\)

Nên \(\widehat {MSO} = \widehat {MOA} hay \widehat {MSD} = \widehat {MOA} (1)\)

Ta có \(\widehat {MOA} = 2\widehat {MBA}\) (góc ở tâm cùng chắn cung AM) (2)

Từ (1) và (2) suy ra \(\widehat {MSD} = 2\widehat {MBA}.\)