Giải Vật lí 10 trang 26 Bài 5: Tốc độ và vận tốc
Giải Vật lí 10 trang 26 Bài 5: Tốc độ và vận tốc
Giải Vật lí 10 trang 26 Bài 5 Tốc độ và vận tốc sách Kết nối tri thức có đáp án chi tiết cho từng bài tập trong sách giáo khoa vật lí 10 KNTT. Mời các em học sinh cùng quý phụ huynh tham khảo.
Vật lí 10 trang 26 bài 5
Khởi động trang 26 SGK Vật lí 10
Trong đời sống, tốc độ và vận tốc là hai đại lượng đều dùng để mô tả sự nhanh chậm của chuyển động. Em đã từng sử dụng hai đại lượng này trong những trường hợp cụ thể nào?
Lời giải
Em đã từng sử dụng hai đại lượng này khi nói:
– Xe máy đi với tốc độ 40 km/h.
– Ca nô chạy với tốc độ 12 m/s.
– Máy bay đang bay theo hướng Bắc với vận tốc 200 m/s.
– Đàn chim đang bay về phía Nam với vận tốc 30 km/h.
Hoạt động trang 26 SGK Vật lí 10
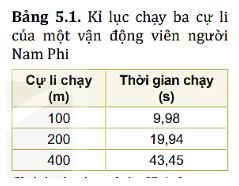
Một vận động viên người Nam Phi đã lập kỉ lục thế giới về chạy ba cự li: 100 m, 200 m và 400 m (Bảng 5.1). Hãy dùng hai cách trên để xác định vận động viên này chạy nhanh nhất ở cự li nào.
Lời giải
Cách 1: So sánh quãng đường đi được trong cùng một thời gian.
– Quãng đường vận động viên chạy được trong 1 s ở mỗi cự li là:
Cách 1: So sánh quãng đường đi được trong cùng một thời gian.
– Quãng đường vận động viên chạy được trong 1 s ở mỗi cự li là:
+ Cự li 100 m: s1 = \(\frac{100}{9,98}\) ≈ 10,02m
+ Cự li 200 m: s2 = \(\frac{200}{19,94}\) ≈ 10,03m
+ Cự li 400 m: s3 = \(\frac{400}{43,45}\) ≈ 9,21m
Trong cùng 1 s, quãng đường vận động viên chạy được ở cự li 200 m lớn nhất.
⇒ Vận động viên chạy nhanh nhất trong cự li 200 m.
Cách 2: So sánh thời gian để đi cùng một quãng đường.
– Thời gian để vận động viên chạy quãng đường 100 m ở mỗi cự li là:
+ Cự li 100 m: t1 = 9,98 s
+ Cự li 200 m: t2 = \(\frac{19,94}2\) ≈ 9,97s
+ Cự li 400 m: t3 = \(\frac{43,45}4\) ≈ 10,68s
Với cùng quãng đường 100 m, thời gian vận động viên chạy ở cự li 200 m ngắn nhất.
⇒ Vận động viên chạy nhanh nhất ở cự li 200 m.
Câu hỏi 1 trang 26 SGK Vật lí 10
Tại sao tốc độ trong công thức (5.1b) được gọi là tốc độ trung bình?
Lời giải
Tốc độ này được gọi là tốc độ trung bình vì đó là tốc độ xét trên quãng đường đủ lớn, trong khoảng thời gian đủ dài. Hơn nữa trên cả quãng đường này, có lúc vật đi với tốc độ cao hơn, có lúc lại đi với tốc độ thấp hơn, nên đây chỉ là tốc độ đại diện cho cả quá trình chuyển động nhanh hay chậm trên quãng đường.
Câu hỏi 2 trang 26 SGK Vật lí 10
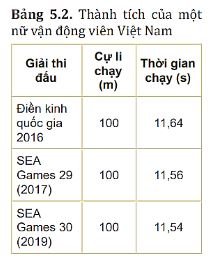
Hãy tính tốc độ trung bình ra đơn vị m/s và km/h của nữ vận động viên tại một số giải thi đấu dựa vào Bảng 5.2.
Lời giải
1.
Công thức 5.1b: \(v = \frac{{\Delta s}}{{\Delta t}}\)
Tốc độ này được gọi là tốc độ trung bình vì nó cho biết quãng đường vật đi được trong một thời gian xác định.
2.
Tốc độ trung bình của nữ vận động viên tại các giải thi đấu là:
– Điền kinh quốc gia 2016:
\(v = \frac{{100}}{{11,64}} = 8,59\left( {m/s} \right) = 30,92\left( {km/h} \right)\)
– SEA Games 29 (2017):
\(v = \frac{{100}}{{11,56}} = 8,65\left( {m/s} \right) = 31,14\left( {km/h} \right)\)
– SEA Games 29 (2019):
\(v = \frac{{100}}{{11,54}} = 8,67\left( {m/s} \right) = 31,21\left( {km/h} \right)\)
Vật lí 10 trang 27 bài 5
Câu hỏi trang 27 SGK Vật lí 10
Bố bạn A đưa A đi học bằng xe máy vào lúc 7 giờ. Sau 5 phút xe đạt tốc độ 30 km/h. Sau 10 phút nữa, xe tăng tốc độ lên thêm 15 km/h. Đến gần trường, xe giảm dần tốc độ và dừng trước cổng trường lúc 7 giờ 30 phút.
a) Tính tốc độ trung bình của xe máy chở A khi đi từ nhà đến trường. Biết quãng đường từ nhà đến trường dài 15 km.
b) Tính tốc độ của xe vào lúc 7 giờ 15 phút và 7 giờ 30 phút. Tốc độ này là tốc độ gì?
Lời giải
a) Thời gian xe máy đi từ nhà đến trường là:
∆t = 7h30 – 7h = 30min = 0,5h
– Tốc độ trung bình của xe máy chở A khi đi từ nhà đến trường:
v = \(\frac{\Delta s}{\Delta t}\) = \(\frac{15}{0,5}\) = 30km/h
b) Theo đề bài ta có:
– Sau 5 phút kể từ khi xuất phát, xe đạt tốc độ 30 km/h.
– Sau 10 phút nữa, xe tăng tốc lên thêm 15 km/h.
⇒ Tốc độ của xe vào lúc 7 giờ 15 phút là: v1 = 15 + 30 = 45 km/h
– Xe dừng trước cổng trường lúc 7 giờ 30 phút.
⇒ Tốc độ của xe lúc 7 giờ 30 phút là: v2 = 0 km/h
– Cả 2 tốc độ này đều là tốc độ tức thời vì lúc này bố bạn A đang đọc số chỉ của tốc kế trên xe máy.
Câu hỏi trang 27 SGK Vật lí 10
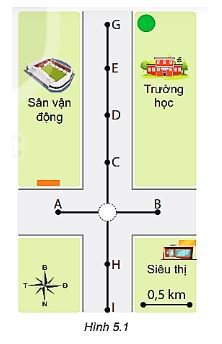
Một người đi xe máy qua ngã tư (Hình 5.1) với tốc độ trung bình 30 km/h theo hướng Bắc. Sau 3 phút người đó đi đến vị trí nào trên hình?
Lời giải
Lời giải
Đổi 3 phút = \(\frac3{60}\) = 0,05 h
Quãng đường người đó đi được trong 3 phút là:
s = v. t = 30 . 0,05 = 1,5 km
⇒ Sau 3 phút đi với vận tốc 30 km/h theo hướng Bắc thì người đó đi đến vị trí E.
Câu hỏi trang 27 SGK Vật lí 10
Vật lí 10 trang 28 bài 5
Theo em, biểu thức nào sau đây xác định giá trị vận tốc? Tại sao?
a) s/t;
b) vt;
c) d/t;
d) d.t
Lời giải
Biểu thức xác định giá trị vận tốc là: v = d/t.
Vì vận tốc được tính bằng độ dịch chuyển của vật trong một đơn vị thời gian.
Câu hỏi trang 28 SGK vật lí 10
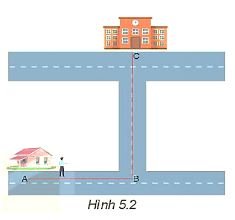
Bạn A đi học từ nhà đến trường theo lộ trình ABC (Hình 5.2). Biết bạn A đi đoạn đường AB = 400 m hết 6 phút, đoạn đường BC = 300 m hết 4 phút. Xác định tốc độ trung bình và vận tốc trung bình của bạn A khi đi từ nhà đến trường.
Lời giải:
– Độ dài quãng đường từ nhà đến trường là:
\(s = AB + BC = 400 + 300 = 700\left( m \right)\)
– Thời gian đi từ nhà đến trường là:
\(t = 6 + 4 = 10\) (phút)
– Tốc độ trung bình của bạn A khi đi từ nhà đến trường là:
\(v = \frac{s}{t} = \frac{{700}}{{10}} = 70(m/phút) \approx 1,167(m/s)\)
– Độ dịch chuyển của bạn A là:
\(d = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{400}^2} + {{300}^2}} = 500\left( m \right)\)
– Vận tốc trung bình của bạn A khi đi từ nhà đến trường là:
\(v = \frac{d}{t} = \frac{{500}}{{6 + 4}} = 50(m/phút) \approx 0,83(m/s)\)
Câu hỏi 1 trang 28 SGK Vật lí 10
Hãy xác định vận tốc của hành khách đối với mặt đường nếu người này chuyển động về cuối đoàn tàu với vận tốc có cùng độ lớn 1 m/s.
Lời giải
Đổi: 36 km/h = 10 m/s
Gọi:
\({\overrightarrow v _{1,2}}\) là vận tốc của hành khách so với tàu
\({\overrightarrow v _{2,3}}\) là vận tốc của tàu so với mặt đường
\({\overrightarrow v _{1,3}}\) là vận tốc của hành khách so với mặt đường
Suy ra, ta có: \({\overrightarrow v _{1,3}} = {\overrightarrow v _{1,2}} + {\overrightarrow v _{2,3}}\)
Do hành khách chuyển động về cuối đoàn tàu, tức là ngược chiều chuyển động của đoàn tàu nên ta có:
\({v_{1,3}} = – {v_{1,2}} + {v_{2,3}} = – 1 + 10 = 9\left( {m/s} \right)\)
Vậy vận tốc của hành khách đối với mặt đường trong trường hợp này là 9 m/s.
Câu hỏi 2 trang 28 SGK vật lí 10
Một người bơi trong bể bơi yên lặng có thể đạt tới vận tốc 1 m/s. Nếu người này bơi xuôi dòng sông có dòng chảy với vận tốc 1 m/s thì có thể đạt vận tốc tối đa là bao nhiêu?
Lời giải
Gọi:
\({\overrightarrow v _{1,2}}\) là vận tốc của người so với nước
\({\overrightarrow v _{2,3}}\) là vận tốc của nước so với bờ
\({\overrightarrow v _{1,3}}\) là vận tốc của người so với bờ
Ta có: \({\overrightarrow v _{1,3}} = {\overrightarrow v _{1,2}} + {\overrightarrow v _{2,3}}\)
– Khi người bơi trong bể nước yên lặng, tức \({v_{2,3}} = 0\), ta có:
\({v_{1,2}} = {v_{1,3}} = 1\left( {m/s} \right)\)
– Khi người này bơi xuôi dòng chảy với vận tốc \({v_{2,3}} = 1\left( {m/s} \right)\), ta có:
\({v_{1,3}} = {v_{1,2}} + {v_{2,3}} = 1 + 1 = 2\left( {m/s} \right)\)
Vậy nếu người này bơi xuôi dòng sông có dòng chảy với vận tốc 1 m/s thì có thể đạt vận tốc tối đa là 2 m/s.
Câu hỏi 3 trang 28 SGK Vật lí 10
Một ca nô chạy hết tốc lực trên mặt nước yên lặng có thể đạt 21,5 km/h. Ca nô này chạy xuôi dòng sông trong 1 giờ rồi quay lại thì phải mất 2 giờ nữa mới về tới vị trí ban đầu. Hãy tính vận tốc chảy của dòng sông.
Lời giải
Gọi:
\({\overrightarrow v _{1,2}}\) là vận tốc của canô so với nước
\({\overrightarrow v _{2,3}}\) là vận tốc của nước so với bờ
\({\overrightarrow v _{1,3}}\) là vận tốc của canô so với bờ
Ta có: \({\overrightarrow v _{1,3}} = {\overrightarrow v _{1,2}} + {\overrightarrow v _{2,3}}\)
– Khi canô chạy trên mặt nước yên lặng, tức \({v_{2,3}} = 0\), ta có:
\({v_{1,2}} = {v_{1,3}} = 21,5\left( {km/h} \right)\)
– Khi canô chạy xuôi dòng sông, ta có:
\(v{‘_{1,3}} = {v_{1,2}} + {v_{2,3}} = 21,5 + {v_{2,3}}\)
\( \Rightarrow {t_1} = \frac{d}{{21,5 + {v_{2,3}}}} \Leftrightarrow 1 = \frac{d}{{21,5 + {v_{2,3}}}} \Leftrightarrow 21,5 = d – {v_{2,3}}\) (1)
– Khi canô quay lại, ta có:
\(v{‘_{1,3}} = {v_{1,2}} – {v_{2,3}} = 21,5 – {v_{2,3}}\)
\( \Rightarrow {t_1} = \frac{d}{{21,5 – {v_{2,3}}}} \Leftrightarrow 2 = \frac{d}{{21,5 – {v_{2,3}}}} \Leftrightarrow 43 = d + 2{v_{2,3}}\) (2)
– Từ (1) và (2) ta suy ra: \(\left\{ \begin{array}{l}d = 28,67\left( {km} \right)\\{v_{2,3}} = 7,17\left( {km/h} \right)\end{array} \right.\)
Vậy vận tốc chảy của dòng sông là 7,17 km/h.
Vật lí 10 trang 29 bài 5
Câu hỏi 1 trang 29 SGK Vật lí 10
Một máy bay đang bay theo hướng Bắc với vận tốc 200 m/s thì bị gió từ hướng Tây thổi vào với vận tốc 20 m/s. Xác định vận tốc tổng hợp của máy bay lúc này.
Lời giải
Gọi:
\({\overrightarrow v _{1,2}}\) là vận tốc của máy bay so với gió
\({\overrightarrow v _{2,3}}\) là vận tốc của gió so với đường bay
\({\overrightarrow v _{1,3}}\) là vận tốc của máy bay so với đường bay
Suy ra:
Vận tốc tổng hợp của máy bay lúc này là:
\({v_{1,3}} = \sqrt {v_{1,2}^2 + v_{2,3}^2} = \sqrt {{{200}^2} + {{20}^2}} = 201\left( {m/s} \right)\)
Câu hỏi 2 trang 29 SGK Vật lí 10
Một người lái máy bay thể thao đang tập bay ngang. Khi bay từ A đến B thì vận tốc tổng hợp của máy bay là 15 m/s theo hướng 60o Đông – Bắc và vận tốc của gió là 7,5 m/s theo hướng Bắc.
Hãy chứng minh rằng khi bay từ A đến B thì người lái phải luôn hướng máy bay về hướng Đông.
Lời giải
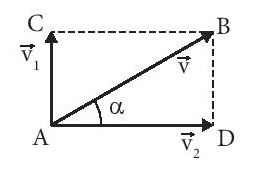
Vận tốc tổng hợp của máy bay: \(\overrightarrow v = \overrightarrow {{v_1}} + \overrightarrow {{v_2}} \)
Vì \(AC = \frac{1}{2}AB\) nên \(\Delta ABC\) và \(\Delta ABD\) đều là một nửa của tam giác đều nên \(\alpha = {30^0}\) và AD là phương nằm ngang theo hướng Đông.
Em có thể 1 trang 29 SGK vật lí 10
Tự xác định được tốc độ chuyển động của mình trong một số trường hợp đơn giản.
Lời giải
Ví dụ:
Quãng đường từ nhà em đến trường dài 5 km. Hằng ngày em đạp xe đến trường mất 20 phút. Tốc độ chuyển động của em là: v = \(\frac st\) = \(\frac{5.1000}{20.60}\) ≈ 4,17m/s
Em có thể 2 trang 29 SGK vật lí 10
Sử dụng đúng các thuật ngữ tốc độ và vận tốc trong các tình huống khác nhau.
Lời giải
Để sử dụng đúng các thuật ngữ tốc độ và vận tốc, em cần phân biệt được tốc độ và vận tốc:
| Tốc độ | Vận tốc |
| – là đại lượng vô hướng. | – là đại lượng vectơ. |
| – được tính bằng thương số của quãng đường và thời gian đi hết quãng đường đó. \(\overrightarrow v\;=\;\frac st\) | – được tính bằng thương số của độ dịch chuyển và khoảng thời gian dịch chuyển. \(\overrightarrow{v\;}=\;\frac dt\) |
| Khi vật chuyển động thẳng theo một hướng thì tốc độ và vận tốc có độ lớn bằng nhau | |
| Ví dụ: ta có thể nói chiếc xe máy chuyển động từ A đến B với tốc độ là 20 km/h. | Ví dụ: ta có thể nói xe máy chuyển động từ vị trí A với vận tốc 20 km/h theo hướng Tây – Bắc để đến vị trí B. |
