Toán 7 tập 1 trang 47 bài 3: Giá trị tuyệt đối của một số thực

Giải toán 7 tập 1 trang 47 bài 3 sách Cánh diều có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 7 Cánh diều. Mời các em học sinh cùng quý phụ huynh tham khảo.

Toán 7 tập 1 trang 44

Khởi động trang 44 toán 7 tập 1

Đề bài

Hình 5 mô tả một vật chuyển động từ điểm gốc O theo chiều ngược với chiều dương của trục số. Sau 1 giờ, vật đến điểm -40 trên trục số (đơn vị đo trên trục số là ki-lô-mét)

Hỏi vật đã chuyển động được quãng đường bao nhiêu ki-lô-mét sau 1 giờ?

Làm thế nào để biểu diễn được quãng đường đó thông qua số thực -40?

Lời giải chi tiết

Vật đã chuyển động được quãng đường là:

0 – (- 40) = 40 (km)

Để biểu diễn được quãng đường đó thông qua số thực -40, ta sử dụng khái niệm giá trị tuyệt đối (|-40|=40)

Hoạt động 1 trang 44 toán 7 tập 1

a) Hãy biểu diễn hai số -5 và 5 trên cùng một trục số.

b) Tính khoảng cách từ điểm 5 đến điểm 0.

c) Tính khoảng cách từ điểm -5 đến điểm 0.

Phương pháp giải:

Vẽ trục số.

Điểm -5 biểu diễn bởi điểm nằm bên trái gốc 0 và cách gốc 0 một khoảng là 5 đơn vị.

Điểm 5 biểu diễn bởi điểm nằm bên phải gốc 0 và cách gốc 0 một khoảng là 5 đơn vị.

Lời giải chi tiết:

a)

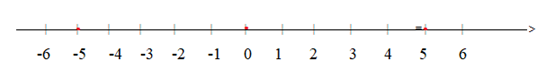
b) Khoảng cách từ điểm 5 đến điểm 0 là: 5 đơn vị

c) Khoảng cách từ điểm – 5 đến điểm 0 là: 5 đơn vị

Toán 7 tập 1 trang 45

Luyện tập vận dụng 1 trang 45 toán 7 tập 1

So sánh giá trị tuyệt đối của hai số thực a,b trong mỗi trường hợp sau:

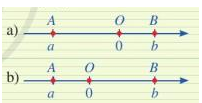
Phương pháp giải:

Giá trị tuyệt đối của 1 số là khoảng cách từ điểm biểu diễn số đó đến điểm 0 trên trục số

Lời giải chi tiết:

a) Ta có: |a| = OA; |b| = OB

Vì OA > OB nên |a| > |b|

b) Ta có: |a| = OA; |b| = OB

Vì OA < OB nên |a| < |b|

Chú ý:

Điểm càng xa gốc 0 thì giá trị tuyệt đối của nó càng lớn

Hoạt động 2 trang 45 toán 7 tập 1

Tìm |x| trong mỗi trường hợp sau:

a) x = 0,5;

b) $x = – \frac{3}{2}$;

c) x = 0;

d) x = -4;

e) x = 4.

Phương pháp giải:

+ Nếu x > 0 thì |x| = x

+ Nếu x < 0 thì |x|= -x

+ Nếu x = 0 thì |x| = 0

Lời giải chi tiết:

$\begin{array}{l}a){\rm{|0,5| = 0,5;}}\\{\rm{b) | – }}\frac{3}{2}| = \frac{3}{2};\\c)|0| = 0;\\d)| – 4| = 4;\\e)|4| = 4\end{array}$

Toán 7 tập 1 trang 46

Luyện tập vận dụng 2 trang 46 toán 7 tập 1

Tìm |-79|; |10,7|; $\left| {\sqrt {11} } \right|;\left| {\frac{{ – 5}}{9}} \right|$

Phương pháp giải:

+ Nếu x > 0 thì |x| = x

+ Nếu x < 0 thì |x|= -x

+ Nếu x = 0 thì |x| = 0

Lời giải chi tiết:

$\left| { – 79} \right| = 79;{\rm{ }}\left| {10,7} \right| = 10,7;$$\left| {\sqrt {11} } \right| = \sqrt {11} ;\left| {\frac{{ – 5}}{9}} \right| = \frac{5}{9}$

Luyện tập vận dụng 3 trang 46 toán 7 tập 1

Cho x = -12. Tính giá trị của mỗi biểu thức sau:

a) 18 + |x|

b) 25 – |x|

c) |3+x| – |7|

Phương pháp giải:

a) ,b) Tìm |x| rồi thay vào từng biểu thức

c) Tính |3 + x| , |7| rồi tính giá trị biểu thức

Lời giải chi tiết:

Vì x = -12 nên |x| = 12

a) 18 + |x| = 18 + 12 = 30;

b) 25 – |x| = 25 – 12 = 13;

c) |3+x| – |7| = |3 + (-12)| – 7 = | 3+(-12)| – 7 = |-9| – 7 = 9 – 7 = 2

Toán 7 tập 1 trang 47

Bài 1 trang 47 Toán 7 tập 1

Tìm: $\left| { – 59} \right|;\left| { – \frac{3}{7}} \right|;\left| {1,23} \right|;\left| { – \sqrt 7 } \right|$

Lời giải::

$\left| { – 59} \right| = 59;\left| { – \frac{3}{7}} \right| = \frac{3}{7};\left| {1,23} \right| = 1,23;\left| { – \sqrt 7 } \right| = \sqrt 7$

Bài 2 trang 47 Toán 7 tập 1

Chọn dấu “<”, “>”, “ =” thích hợp cho vào chỗ trống

a. $\left | 2,3 \right |$ $\left | -\frac{13}{6} \right |$

b. 9 $\left | -14 \right |$

c. $\left | -7,5 \right |$ -7,5

Lời giải::

a. $\left | 2,3 \right | > \left | -\frac{13}{6} \right |$

b. $9 < \left | -14 \right |$

c. $\left | -7,5 \right | > -7,5$

Bài 3 trang 47 Toán 7 tập 1

Tính giá trị biểu thức:

a) |-137| + |-363|;

b) |-28| – |98|;

c) (-200) – |-25|.|3|

Lời giải::

a) $|-137| + |-363|=137 + 363 = 500$;

b) $|-28| – |98| = 28 – 98 = -(98 – 28) = – 70$;

c) $(-200) – |-25|.|3| = (-200) – 25 . 3 = (-200) – 75 = -(200 + 75) = -275$

Bài 4 trang 47 Toán 7 tập 1

Tìm x, biết:

a) |x| = 4;

b) |x| = $\sqrt 7 ;$

c) |x+5| = 0;

d) $\left| {x – \sqrt 2 } \right| = 0$

Lời giải::

a) |x| = 4

$\left[ {_{x = – 4}^{x = 4}} \right.$

Vậy $x \in \{ 4; – 4\}$

b) $|x| = \sqrt 7$

$\left[ {_{x = – \sqrt 7 }^{x = \sqrt 7 }} \right.$

Vậy $x \in \{ \sqrt 7 ; – \sqrt 7 \}$

c) ) |x+5| = 0

x+5 = 0

x = -5

Vậy x = -5

$d) \left| {x – \sqrt 2 } \right| = 0$

$x – \sqrt 2 = 0$

$x = \sqrt 2$

Vậy $x = \sqrt 2$

Bài 5 trang 47 Toán 7 tập 1

Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Giá trị tuyệt đối của một số thực là một số dương.

b) Giá trị tuyệt đối của một số thực là một số không âm.

c) Giá trị tuyệt đối của một số thực là số đối của nó.

d) Hai số đối nhau có giá trị tuyệt đối bằng nhau.

Lời giải::

a) Giá trị tuyệt đối của một số thực là một số dương.

Phát biểu trên sai vì giá trị tuyệt đối của số 0 là 0 mà số 0 không phải là số dương.

b) Giá trị tuyệt đối của một số thực là một số không âm.

Phát biểu trên đúng vì giá trị tuyệt đối của một số là khoảng cách của số đó đến điểm 0 nên nó không thể âm.

c) Giá trị tuyệt đối của một số thực là số đối của nó.

Phát biểu trên sai vì 1,3 là số thực và giá trị tuyệt đối của 1,3 là 1,3.

d) Hai số đối nhau thì có giá trị tuyệt đối bằng nhau.

Phát biểu trên đúng vì khoảng cách của hai số đối nhau đến 0 là bằng nhau.

Bài 6 trang 47 Toán 7 tập 1

So sánh hai số a và b trong mỗi trường hợp sau:

a) a, b là hai số dương và |a| < |b|;

b) a, b là hai số âm và |a| < |b|

Lời giải::

a) Khi a, b là hai số dương:

|a| = a; |b| = b

Khi đó, |a| < |b| , tức là a < b

Vậy a < b

b) Khi a, b là hai số âm:

|a| = – a; |b| = – b

Khi đó, |a| < |b| , tức là – a < – b hay a > b

Vậy a > b