Giải toán 7 tập 1 trang 36 bài 7 sách Kết nối tri thức có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 7 Kết nối tri thức mới. Mời các em học sinh cùng quý phụ huynh tham khảo.

Toán 7 tập 1 trang 36 Bài 7: Tập hợp các số thực

Giải toán 7 tập 1 trang 36 bài 7 sách Kết nối tri thức có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 7 Kết nối tri thức mới. Mời các em học sinh cùng quý phụ huynh tham khảo.

1. Khái niệm số thực và trục số thực

Trang 33 Toán 7 tập 1

Luyện tập 1 trang 33 Toán 7 tập 1

a) Trong các cách viết: $\sqrt 2 \in \mathbb{Q}; \pi \in \mathbb{I}; 15 \in \mathbb{R}$,

cách viết nào đúng?

b) Viết số đối của các số: 5,08(299);$ – \sqrt 5$

Hướng dẫn giải

a) Ta có: $\sqrt 2 \notin \mathbb{Q};\pi \in \mathbb{I};15 \in \mathbb{R}$

Vậy cách viết $\pi \in \mathbb{I}; 15 \in \mathbb{Q}$ là đúng

b) Số đối của 5,08(299) là -5,08(299)

Số đối của $-\sqrt 5$ là $\sqrt 5$

Trang 34 Toán 7 tập 1

Câu hỏi trang 34 Toán 7 tập 1

Điểm nào trong Hình 2.4 biểu diễn số – 4\sqrt 2$ ? Em có nhận xét gì về điểm biểu diễn của hai số đối nhau?

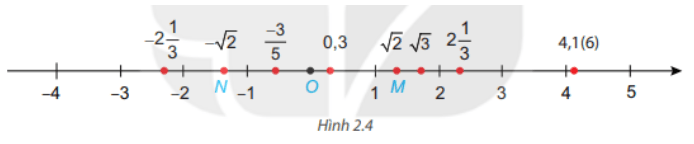
Hướng dẫn giải

Điểm biểu diễn số – $\sqrt 2$ là điểm N.

Điểm biểu diễn của hai số đối nhau là 2 điểm cách đều gốc O và nằm về 2 phía của điểm O

Luyện tập 2 trang 34 Toán 7 tập 1

Cho biết nếu một tam giác vuông có hai cạnh góc vuông bằng 1 và 3 thì cạnh huyền của tam giác bằng $\sqrt {10}$ . Em hãy vẽ điểm biểu diễn số – $\sqrt {10}$ trên trục số.

Hướng dẫn giải

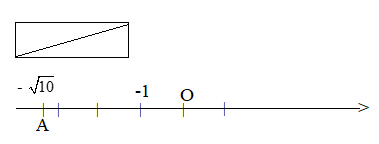
Chú ý: Các số thực âm được biểu diễn bởi các điểm nằm bên trái điểm O trên trục số.

2. Thứ tự trong tập hợp các số thực

Luyện tập 3 trang 35 Toán 7 Tập 1:

So sánh:

a) 1,313233… và 1,(32);

b) $\sqrt{55}$ và 2,36 (có thể dùng máy tính cầm tay để tính √55)

Hướng dẫn giải

a) 1,(32) = 1,323232… nên 1,313233… < 1,323232… hay 1,313233… < 1,(32).

Vậy 1,313233… < 1,(32).

b) Sử dụng máy tính cầm tay tính $\sqrt{55}$ ta được kết quả là 2,236067977.

Làm tròn kết quả với độ chính xác 0,005 được $\sqrt{5}$≈2,24

Do 2,24 < 2,36 nên $\sqrt{5}$ < 2, 36.5 < 2,36.

Vậy $\sqrt{5}$< 2,36.

3. Giá trị tuyệt đối của một số thực

Trang 35 Toán 7 tập 1

Hoạt động 1 trang 35 Toán 7 Tập 1:

Biểu diễn các số 3 và –2 trên trục số rồi cho biết mỗi điểm ấy cách gốc O bao nhiêu đơn vị.

Hướng dẫn giải

Điểm A và B lần lượt là hai điểm biểu diễn các số 3 và –2 trên trục số.

Điểm B cách gốc O một khoảng bằng 2 đơn vị, điểm A cách gốc O một khoảng bằng 3 đơn vị.

Hoạt động 2 trang 35 Toán 7 Tập 1:

Không vẽ hình, hãy cho biết khoảng cách của mỗi điểm sau đến gốc O: –4; –1; 0; 1; 4.

Hướng dẫn giải

Khoảng cách từ –4 đến gốc O là 4 đơn vị.

Khoảng cách từ –1 đến gốc O là 1 đơn vị.

Khoảng cách từ 0 đến gốc O là 0 đơn vị.

Khoảng cách từ 1 đến gốc O là 1 đơn vị.

Khoảng cách từ 4 đến gốc O là 4 đơn vị.

Câu hỏi trang 35 Toán 7 Tập 1:

Từ hoạt động 1 và hoạt động 2, hãy tìm giá trị tuyệt đối của các số: 3; –2; 0; 4 và –4.

Hướng dẫn giải

Giá trị tuyệt đối của 3 là |3|=3.

Giá trị tuyệt đối của –2 là |−2|=2.

Giá trị tuyệt đối của 0 là |0|=0.

Giá trị tuyệt đối của 4 là |4|=4.

Giá trị tuyệt đối của –4 là |−4|=4.

Trang 36 Toán 7 tập 1

Câu hỏi trang 36 Toán 7 Tập 1:

Minh viết: |−2,5|=−2,5 đúng hay sai?

Hướng dẫn giải:

Minh viết |−2,5|=−2,5 là sai vì |−2,5| = 2,5

Chú ý:

Giá trị tuyệt đối của một số thực luôn không âm

Luyện tập 4 trang 36 Toán 7 Tập 1:

Tính:

a) |-2,3|

b) $\left| {\frac{7}{5}} \right|$

c) |-11|

d) $\left| { – \sqrt 8 } \right|$

Hướng dẫn giải

a) |-2,3| = 2,3

b) $\left| {\frac{7}{5}} \right| = \frac{7}{5}$

c) |-11| = 11

d) $\left| { – \sqrt 8 } \right| = \sqrt 8$

Thử thách nhỏ trang 36 Toán 7 Tập 1:

Liệt kê các phần tử của tập hợp A = $\left\{ {x|x \in \mathbb{Z},\left| x \right| < 5} \right\}$

Hướng dẫn giải

Ta có:

|x| < 5, x là số nguyên

=> x ∈ {-4; -3; -2; -1; 0; 1; 2; 3; 4}

Liệt kê các phần tử của tập hợp A là: A = {-4; -3; -2; -1; 0; 1; 2; 3; 4}

4. Giải bài tập trang 36 Toán 7 tập 1

Bài 2.13 trang 36 Toán 7 tập 1

Xét tập hợp A = $\left\{ {7,1; – 2,(61);0;5,14;\frac{4}{7};\sqrt {15} ; – \sqrt {81} } \right\}$

. Bằng cách liệt kê phần tử, hãy viết tập hợp B gồm các số hữu tỉ thuộc tập A và tập hợp C gồm các số vô tỉ

Hướng dẫn giải

B = $\left\{ {7,1; – 2,(61);0;5,14;\frac{4}{7}; – \sqrt {81} } \right\}$

C = $\left\{ {\sqrt {15} } \right\}$

Bài 2.14 trang 36 Toán 7 tập 1

Gọi A’ là tập hợp các số đối của các số thuộc tập A trong bài tập 2.13. Liệt kê các phần tử của A’

Hướng dẫn giải

Số đối của số 7,1 là -7,1

Số đối của số -2,(61) là 2,(61)

Số đối của số 0 là 0

Số đối của số 5,14 là -5,14

Số đối của số $\frac{4}{7}$ là – $\frac{4}{7}$

Số đối của số $\sqrt {15}$ là – $\sqrt {15}$

Số đối của số – $\sqrt {81} = \sqrt {81}$

Bài 2.15 trang 36 Toán 7 tập 1

Mũi tên màu xanh trong mỗi hình sau chỉ số thực nào?

Hướng dẫn giải

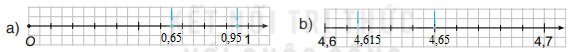
Bài 2.16 trang 36 Toán 7 tập 1

Tính:

a)$\left| { – 3,5} \right|$;

b)$\left| {\frac{{ – 4}}{9}} \right|$;

c)$\left| 0 \right|$;

d)$\left| {2,0(3)} \right|$.

Hướng dẫn giải

$\begin{array}{l}a)\left| { – 3,5} \right| = 3,5;\\b)\left| {\frac{{ – 4}}{9}} \right| = \frac{4}{9};\\c)\left| 0 \right| = 0;\\d)\left| {2,0(3)} \right| = 2,0(3)\end{array}$

Chú ý:

Nếu $a \ge 0$ thì $\left| a \right| = a$

Nếu a < 0 thì $\left| a \right|$ = – a

Bài 2.17 trang 36 Toán 7 tập 1

Xác định dấu và giá trị tuyệt đối của mỗi số sau:

a) a = 1,25;

b) b = – 4,1;

c) c = – 1,414213562….

Hướng dẫn giải

a) a = 1,25 có dấu dương, $\left| a \right| = \left| {1,25} \right|$ = 1,25

b) b = – 4,1 có dấu âm, $\left| b \right| = \left| { – 4,1} \right|$ = 4,1

c) c = – 1,414213562…. có dấu âm,$\left| c \right| = \left| { – 1,414213562….} \right|$ = 1,414213562….

Bài 2.18 trang 36 Toán 7 tập 1

Tìm tất cả các số thực x thỏa mãn điều kiện \left| x \right| = 2,5

Hướng dẫn giải

Nếu x ≥ 0 thì |x| = x, mà |x| = 2,5 nên x = 2,5.

Nếu x < 0 thì |x|= −x, mà |x| = 2,5 nên –x = 2,5 do đó x = –2,5.

Vậy x = –2,5 hoặc x = 2,5.