Toán 7 tập 1 trang 86 Luyện tập chung

Giải toán 7 tập 1 trang 86 bài luyện tập chung có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 7 Kết nối tri thức mới. Mời các em học sinh cùng quý phụ huynh tham khảo.

Trang 86 Toán 7 tập 1

Bài 4.29 trang 86 Toán 7 Kết nối tri thức

Cho Hình 4.73. Hãy tính các độ dài a, b và số đo x, y của các góc trên hình vẽ.

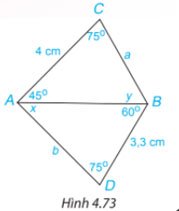
Hướng dẫn giải:

Xét tam giác ABC có:

Hướng dẫn giải:

Xét tam giác ABC có:

$widehat {BAC} + \widehat {ABC} + \widehat C = {180^o}$

$ \Rightarrow {45^o} + y + {75^o} = {180^o}$

$\Rightarrow y = {60^o}$

Xét tam giác ABD có:

$\widehat {DAB} + \widehat {DBA} + \widehat D = {180^o}$

$\Rightarrow x + {60^o} + {75^o} = {180^o}$

$\Rightarrow x = {45^o}$

Xét 2 tam giác ABC và ADB có:

$\widehat {DAB} = \widehat {CAB} = {45^o}$

AB chung

$\widehat D = \widehat C = {75^o}$

=>$\Delta ABC = \Delta ADB$(g.c.g)

=>BC=BD (2 cạnh tương ứng), mà BD = 3,3 cm =>a= BC= 3,3cm

AC=AD (2 cạnh tương ứng), mà AC = 4 cm =>b = AD = 4cm

Bài 4.30 trang 86 Toán 7 Kết nối tri thức

Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM =ON, OA > OM.

Chứng minh rằng:

a) $\Delta OAN = \Delta OBM$ ;

b) $\Delta AMN = \Delta BNM$ .

Hướng dẫn giải:

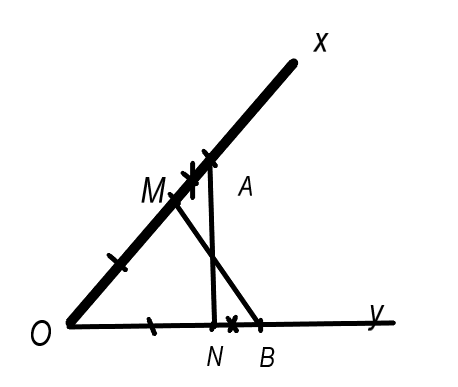
a. Xét ΔOAN và ΔOBM, ta có :

• OA = OB
• Góc O chung
• OM= ON

=> ΔOAN=ΔOBM(c−g−c)

b. Từ câu a => AN= BM. Mà OA = OB=> AM =BN

Xét ΔAMN và ΔBNM, ta có :

• AN= BM
• AM = BN
• MN chung

=> ΔAMN=ΔBNM(c−c−c)

Bài 4.31 trang 86 Toán 7 Kết nối tri thức

Cho Hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng:

a) AC = BD;

b)  ΔACD=ΔBDC.

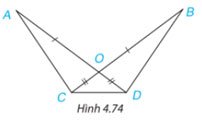
Hướng dẫn giải:

a) Ta có: OA = OB, OC = OD nên AD=BC

Do OC=OD nên tam giác OCD cân => $\widehat {OCD} = \widehat {ODC}$

Xét 2 tam giác ACD và BDC có:

AD=BC

$\widehat {OCD} = \widehat {ODC}$

CD chung
=>ΔACD=ΔBCD(c.g.c)

=>AC=BD (hai cạnh tương ứng)

b) Xét hai tam giác ACD và BDC có:

AO=BO

CO=DO

AC=BD

=>ΔACD=ΔBDC(c.c.c)

Bài 4.32 trang 86 Toán 7 Kết nối tri thức

Cho tam giác MBC vuông tại M có B^=60°. Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.

Hướng dẫn giải:

Xét 2 tam giác vuông CMB và CMA có:

MC chung

MB=MA

=>ΔCMB=ΔCMA(c.g.c)

=>CA = CB (2 cạnh tương ứng).

=> Tam giác ABC cân tại C.

Mà góc B bằng 60^o

=>Tam giác ABC đều.