Toán 7 tập 2 trang 92 Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc

Giải toán 7 tập 2 trang 92 bài 6 sách Cánh diều có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 7 Cánh diều. Mời các em học sinh cùng quý phụ huynh tham khảo.

Toán 7 tập 2 trang 88

Khởi động trang 88 Toán 7 tập 2

Có hai trạm quan sát A, B và một trạm quan sát C ở giữa hồ. Do không thể đo trực tiếp được khoảng cách từ A và từ B đến C nên người ta làm như sau (Hình 55):

–        Đo góc BAC được 60°, đo góc ABC được 45°;

–        Kẻ tia Ax sao cho$\widehat {BAx} = 60^\circ$, kẻ tia By sao cho$\widehat {ABy} = 45^\circ$, xác định giao điểm D của hai tia đó;

–        Đo khoảng cách AD và BD.

Tại sao lại có AC = AD và BC = BD?

Lời giải:

Xét tam giác ABC và ABD có:

$\widehat{ABC}=\widehat{ABD} (=45^0)$

AB chung

$\widehat{BAC}=\widehat{BAD} (=60^0)$

$\Rightarrow \Delta ABC = \Delta ABD$.

Vậy AC = AD và BC = BD. (2 cạnh tương ứng)

HĐ 2 trang 88 toán 7 tập 2

Cho hai tam giác ABC và A’B’C’ (Hình 57) có:$\widehat A = \widehat {A’} = 60^\circ$, AB = A’B’ = 3 cm,$\widehat B = \widehat {B’} = 45^\circ$. Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?

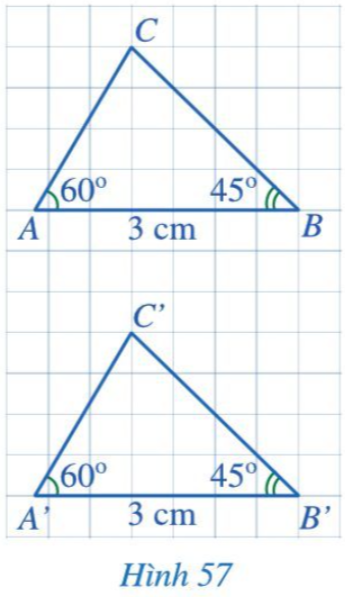
Lời giải:

BC = B’C’ = 4 (đường chéo của 4 ô vuông).

Tam giác ABC và tam giác A’B’C’ có: BC = B’C’, AB = A’B’,$\widehat B = \widehat {B’}$.

Vậy$\Delta ABC = \Delta A’B’C’$(c.g.c)

LT – VD 1 trang 88 toán 7 tập 2

Cho hai tam giác ABC và A’B’C’ thỏa mãn: BC = B’C’ = 3 cm,$\widehat B = \widehat {B’} = 60^\circ ,\widehat C = 50^\circ ,\widehat {A’} = 70^\circ$. Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?

Lời giải:

Tổng ba góc trong một tam giác bằng 180°. Vậy trong tam giác A’B’C’ có$\widehat {C’} = 180^\circ  – 70^\circ  – 60^\circ  = 50^\circ$.

Xét hai tam giác ABC và A’B’C’ có:

$\widehat B = \widehat {B’} = 60^\circ ;$

BC = B’C’ ( = 3 cm)

$\widehat C = \widehat {C’} = 50^\circ$

Vậy$\Delta ABC = \Delta A’B’C’$(g.c.g)

LT – VD 2 trang 88 toán 7 tập 2

Giải thích bài toán ở phần mở đầu.

Lời giải:

Xét hai tam giác ABC và ABD có:$\widehat {CAB} = \widehat {DAB} = 60^\circ ,\widehat {ABC} = \widehat {ABD} = 45^\circ$, AB chung.

Vậy$\Delta ABC = \Delta ABD$ (g.c.g).

Suy ra AC = AD và BC = BD ( 2 cạnh tương ứng)

Toán 7 tập 2 trang 91

Bài 1 trang 91 toán 7 tập 2

Cho hai tam giác ABC và A’B’C’ thỏa mãn: AB = A’B’,$\widehat A = \widehat {A’},\widehat C = \widehat {C’}$. Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?

Lời giải:

Vì$\widehat A = \widehat {A’},\widehat C = \widehat {C’}$mà tổng ba góc trong một tam giác bằng 180° nên$\widehat B = \widehat {B’}$.

Xét hai tam giác ABC và A’B’C’ có:$\widehat A = \widehat {A’}$, AB = A’B’,$\widehat B = \widehat {B’}$.

Vậy$\Delta ABC = \Delta A’B’C’$(g.c.g)

Bài 2 trang 91 toán 7 tập 2

Cho Hình 65 có AM = BN,$\widehat A = \widehat B$. Chứng minh: OA = OB, OM = ON.

Lời giải:

Ta có:$\widehat A = \widehat B$

Mà 2 góc này ở vị trí so le trong nên AM // BN

$\Rightarrow \widehat M = \widehat N$(2 góc so le trong).

Xét hai tam giác AOM và BON có:$\widehat A = \widehat B$, AM = BN,$\widehat M = \widehat N$.

Vậy$\Delta AOM = \Delta BON$ (g.c.g)

Do đó OA = OB, OM = ON. (2 cạnh tương ứng).

Toán 7 tập 2 trang 92

Bài 3 trang 92 Toán 7 tập 2

Cho Hình 66 có$\widehat N = \widehat P = 90^\circ ,\widehat {PMQ} = \widehat {NQM}$. Chứng minh MN = QP, MP = QN.

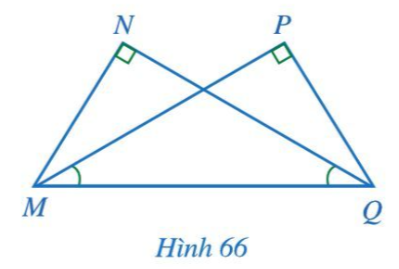
Lời giải:

Ta có: tổng ba góc trong một tam giác bằng 180° và$\widehat N = \widehat P = 90^\circ ,\widehat {PMQ} = \widehat {NQM}$ nên$\widehat {PQM} = \widehat {NMQ}$.

Xét hai tam giác MNQ và QPM có:

$\widehat {NQM}=\widehat {PMQ}$

MQ chung

$\widehat {NMQ}=\widehat {PQM}$

Vậy$\Delta MNQ = \Delta QPM$(g.c.g). Do đó MN = QP, MP = QN ( 2 cạnh tương ứng)

Bài 4 trang 92 Toán 7 tập 2

Cho Hình 67 có$\widehat {AHD} = \widehat {BKC} = 90^\circ ,DH = CK,\widehat {DAB} = \widehat {CBA}$. Chứng minh AD = BC.

Lời giải:

Ta có:$\widehat {DAB} = \widehat {CBA}$

Mà$\widehat {DAB} +\widehat {HAD} =180^0; \widehat {CBA}= \widehat {KBC}$ (2 góc kề bù)

$\Rightarrow \widehat {HAD} = \widehat {KBC}$

Mà tổng ba góc trong tam giác bằng 180° và$\widehat {AHD} = \widehat {BKC} = 90^\circ ,\widehat {HAD} = \widehat {KBC}$ nên$\widehat {ADH} = \widehat {BCK}$.

Xét tam giác AHD và tam giác BKC có:

$\widehat {AHD} = \widehat {BKC}$;

HD = KC;

$\widehat {ADH} = \widehat {BCK}$.

Vậy$\Delta AHD = \Delta BKC$(g.c.g) nên AD = BC ( 2 cạnh tương ứng)

Giải bài 5 trang 92 Toán 7 tập 2

Cho tam giác ABC có $\widehat B > \widehat C$. Tia phân giác góc BAC cắt cạnh BC tại điểm D.

a) Chứng minh$\widehat {ADB} < \widehat {ADC}$.

b) Kẻ tia Dx nằm trong góc ADC sao cho$\widehat {ADx} = \widehat {ADB}$. Giả sử tia Dx cắt cạnh AC tại điểm E. Chứng minh:$\Delta ABD = \Delta AED,AB < AC$.

b) Chứng minh$\Delta ABD = \Delta AED$ theo trường hợp g.c.g và AB < AC vì cạnh đối diện với góc lớn hơn thì lớn hơn.

Lời giải:

a) Ta có:$\widehat {BAD} = \widehat {CAD}$(vì AD là phân giác của góc BAC).

Mà$\widehat B > \widehat C$nên$\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}$.

Tổng ba góc trong một tam giác bằng 180° nên:

$\begin{array}{l}\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\\ \to 180^\circ  – (\widehat B + \widehat {BAD}) < 180^\circ  – (\widehat C + \widehat {CAD})\\ \to \widehat {ADB} < \widehat {ADC}\end{array}$

b) Xét hai tam giác ADB và tam giác ADE có:

$\widehat {ADB} = \widehat {ADE}$;

AD chung;

$\widehat {BAD} = \widehat {EAD}$.

Vậy$\Delta ABD = \Delta AED$ (g.c.g)

Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn.

Trong tam giác ABC có$\widehat B > \widehat C$ nên AC > AB hay AB < AC (AB là cạnh đối diện với góc C, AC là cạnh đối diện với góc B).

Giải bài 6 trang 92 Toán 7 tập 2 – Cánh diều

Cho$\Delta ABC = \Delta MNP$. Tia phân giác của góc BAC và NMP lần lượt cắt các cạnh BC và NP tại D, Q. Chứng minh AD = MQ.

Lời giải:

Ta có:$\Delta ABC = \Delta MNP$ nên theo tính chất 2 tam giác bằng nhau, ta có:

$\begin{array}{l}\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\\AB = MN,BC = NP,AC = NP.\end{array}$

Mà AD và MQ lần lượt là phân giác của góc BAC và NMP nên$\widehat {BAD} = \widehat {NMQ} = \dfrac{1}{2}\widehat {BAC} = \dfrac{1}{2}\widehat {NMP}$.

Xét hai tam giác ABD và MNQ có:

$\widehat {BAD} = \widehat {NMQ}$;

AB = MN;

$\widehat B = \widehat N$.

Vậy$\Delta ABD = \Delta MNQ$ (g.c.g) nên AD = MQ ( 2 cạnh tương ứng)