Giải Toán 7 tập 2 bài 28: Phép chia đa thức một biến
Giải Toán 7 tập 2 bài 28: Phép chia đa thức một biến
Giải toán 7 tập 2 bài 28 sách Kết nối tri thức có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 7 Kết nối tri thức mới. Mời các em học sinh cùng quý phụ huynh tham khảo.
Giải Toán 7 tập 2 bài 28 trang 43
Bài 7.30 trang 43 Toán 7 tập 2
Tính:
a) 8x5 : 4x3
b) 120x7 : (-24x5)
c) $\dfrac{3}{4}{( – x)^3}:\dfrac{1}{8}x$
d) -3,72x 4 : (-4x 2)
Hướng dẫn giải:
a) 8x5 : 4x3 = (8 : 4) . (x5 : x3) = 2.x2
b) 120x7 : (-24x5) = [120 : (-24)] . (x7 : x5) = -5.x2
c) $\dfrac{3}{4}{( – x)^3}:\dfrac{1}{8}x = \dfrac{{ – 3}}{4}{x^3}:\dfrac{1}{8}x = \left( {\dfrac{{ – 3}}{4}:\dfrac{1}{8}} \right).({x^3}:x) = – 6{x^2}$
d) -3,72x 4 : (-4x 2 ) = [(-3,72) : (-4)] . (x 4 : x 2 ) = 0,93x 2
Bài 7.31 trang 43 Toán 7 tập 2
Thực hiện các phép chia đa thức sau:
a) $(-5x^3 + 15x^2 + 18x) : (-5x)$ ;
b) $(-2x^5 – 4x^3 + 3x^2) : 2x^2$ .
Hướng dẫn giải:
a) $(-5x^3 + 15x^2 + 18x) : (-5x)$
= $(-5x^3) : (-5x) + 15x^2 : (-5x) + 18x : (-5x)$
= $x^2 – 3x – \frac{18}{5}$
b) $(-2x^5 – 4x^3 + 3x^2) : 2x^2$
= $(-2x^5 : 2x^2) + (-4x^3 : 2x^2) + (3x^2 : 2x^2)$
= $-x^3 – 2x – \frac{3}{2}$
Bài 7.32 trang 43 Toán 7 tập 2
Thực hiện các phép chia đa thức sau bằng cách đặt tính chia:
a) $(6x^3 – 2x^2 – 9x + 3) : (3x – 1)$ ;
b) $(4x^4 + 14x^3 – 21x – 9) : (2x^2 – 3)$ .
Hướng dẫn giải:
a) $(6x^3 – 2x^2 – 9x + 3) : (3x – 1)$ ;
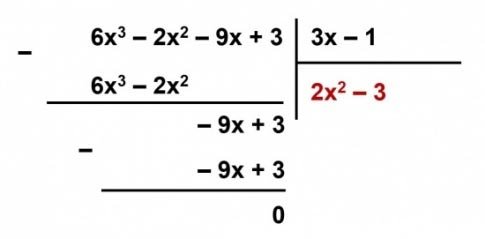
b) $(4x^4 + 14x^3 – 21x – 9) : (2x^2 – 3)$
.
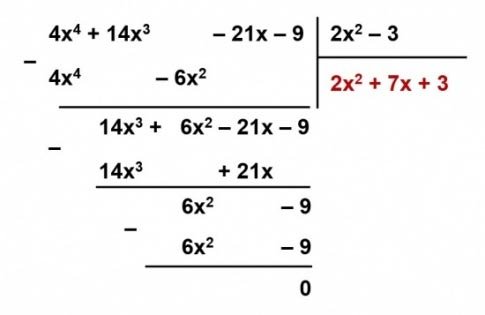
Bài 7.33 trang 43 Toán 7 tập 2
Thực hiện phép chia $0,5x^5 + 3,2x^3 – 2x^2$ cho $0,25x^n$ trong mỗi trường hợp sau:
a) n = 2;
b) n = 3.
Hướng dẫn giải:
a) n = 2
$(0,5x^5 + 3,2x^3 – 2x^2) : 0,25x^2$
= $(0,5x^5 : 0,25x^2) + (3,2x^3 : 0,25x^2) + (– 2x^2 : 0,25x^2)$
= $2x^3 + 12,8x – 8$
b) n = 3
$(0,5x^5 + 3,2x^3 – 2x^2) : 0,25x^3$
= $(0,5x^5 : 0,25x^3) + (3,2x^3 : 0,25x^3) + (– 2x^2 : 0,25x^3)$
= $2x^2 + 12,8 – \frac{8}{x}$
Bài 7.34 trang 43 Toán 7 tập 2
Trong mỗi trường hợp sau đây, tìm thương Q(x) và dư R(x) trong phép chia F(x) cho G(x) rồi biểu diễn F(x) dưới dạng:
F(x) = G(x) . Q(x) + R(x).
a) F(x) = $6x^4 – 3x^3 + 15x^2 + 2x – 1; G(x) = 3x^2$ .
b) F(x) = $12x^4 + 10x^3 – x – 3; G(x) = 3x^2 + x + 1$ .
Hướng dẫn giải:
a) $(6x^4 – 3x^3 + 15x^2 + 2x – 1) : 3x^2$
* Cách 1: Phân tích ta thấy (2x – 1) có bậc nhỏ hơn $3x^2$ nên (2x – 1) là số dư R(x) của đa thức trên.
= $(6x^4 – 3x^3 + 15x^2) : 3x^2$
= $(6x^4 : 3x^2) + (– 3x^3 : 3x^2) + (15x^2 : 3x^2)$
= $2x^2 – x + 5$
* Cách 2: Đặt tính:
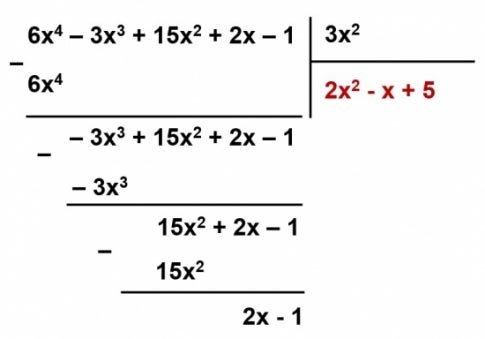
* Vậy: R(x) = 2x – 1
Q(x) = $2x^2 – x + 5$
F(x) = $3x^2 . (2x^2 – x + 5) + 2x – 1$
b) $(12x^4 + 10x^3 – x – 3) : (3x^2 + x + 1)$
.
Đặt tính:
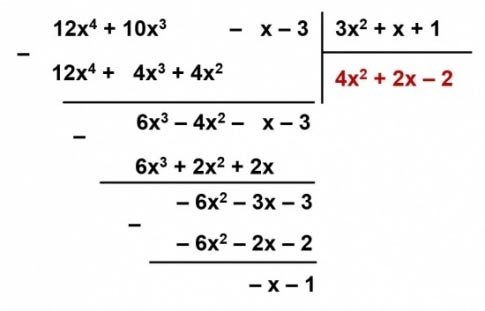
Vậy: R(x) = – x – 1
Q(x) = $4x^2 + 2x – 2$
F(x) = $(3x^2 + x + 1) . (4x^2 + 2x – 2) – x – 1$
Bài 7.35 trang 43 Toán 7 tập 2
Bạn Tâm lúng túng khi muốn tìm thương và dư trong phép chia đa thức 21x – 4 cho 3x^2. Em có thể giúp bạn Tâm được không?
Hướng dẫn giải:
Phân tích ta thấy (21x – 4) có bậc nhỏ hơn $3x^2$ nên (21x – 4) của đa phép chia đa thức 21x – 4 cho $3x^2$ .
* Vậy: Phép chia đa thức 21x – 4 cho $3x^2$ có:
Thương là 0. Số dư là (21x – 4).
