Giải Toán 7 tập 2 bài 32: Quan hệ giữa đường vuông góc và đường xiên
Giải Toán 7 tập 2 bài 32: Quan hệ giữa đường vuông góc và đường xiên
Giải toán 7 tập 2 bài 32 sách Kết nối tri thức có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 7 Kết nối tri thức mới. Mời các em học sinh cùng quý phụ huynh tham khảo.
Giải Toán 7 tập 2 bài 32 trang 64
Hoạt động trang 64 Toán 7 tập 2
Cho điểm A không nằm trên đường thẳng d.
a) Hãy vẽ đường vuông góc AH và một đường xiên AM từ A đến d.
b) Em hãy giải thích vì sao AH < AM.
Hướng dẫn giải
a) Hình vẽ minh họa

b) Ta có: AH ⊥ d => $\widehat {MHA} = {90^0}$
=> $\widehat {MHA}$ là góc lớn nhất trong ∆AHM
=> Cạnh AM là cạnh lớn nhất trong ∆AHM.
=> AH < AM
Luyện tập trang 64 Toán 7 tập 2
Cho hình vuông ABCD có độ dài cạnh bằng 2 cm, M là một điểm trên cạnh BC như Hình 9.10.
a) Hãy chỉ ra các đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BC.
b) So sánh hai đoạn thẳng AB và AM.
c) Tìm khoảng cách từ điểm C đến đường thẳng AB.

Hướng dẫn giải
a) Đường vuông góc kẻ từ A đến đường thẳng BC là AB.
Đường xiên kẻ từ A đến đường thẳng BC là AM.
b) Do AM là đường xiên kẻ từ A đến BC và AB là đường vuông góc kẻ từ A đến BC nên AM > AB.
c) Khoảng cách từ C đến đường thẳng AB bằng độ dài đoạn BC.
Do ABCD là hình vuông nên BC = AD = 2 cm.
Vậy khoảng cách từ C đến đường thẳng AB bằng 2 cm.
Vận dụng trang 64 Toán lớp 7 Tập 2
Em hãy trả lời câu hỏi trong tình huống mở đầu.
Hướng dẫn giải
Ta có OA là đường vuông góc kẻ từ O đến AC.
OB và OC là các đường xiên kẻ từ O đến AC nên OB > OA và OC > OA.
Do đó để bơi sang bờ bên kia nhanh nhất thì Nam nên chọn đường bơi OA.
Thử thách trang 64 Toán lớp 7 Tập 2
a) Quan sát Hình 9.11, ta thấy khi M thay đổi trên d, M càng xa H thì độ dài AM càng lớn, tức là nếu HM < HN thì AM < AN. Hãy chứng minh khẳng định này nhờ quan hệ giữa góc và cạnh đối diện trong tam giác AMN.
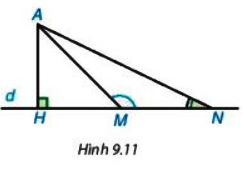
b) Xét hình vuông ABCD và một điểm M tùy ý nằm trên các cạnh của hình vuông. Hỏi với vị trí nào của M thì AM lớn nhất? Vì sao?
Hướng dẫn giải
a) Với HM < HN ta có:
$\widehat {NMA} = \widehat {MHA} + \widehat {MAH} > \widehat {MHA}$
(Do $\widehat {NMA}$ là góc ngoài tại đỉnh M của ∆AHM)
=> $\widehat {NMA}$ là góc tù
=> $\widehat {NMA}$ là góc lớn nhất trong ∆AMN
=> Cạnh AN là cạnh lớn nhất trong ∆AMN
=> AM < AN
b)

Nếu M nằm trên AB hoặc AD thì AM ≤ AB (*)
Nếu M nằm trên BC hoặc CD thì AM ≤ AC (**)
Ta lại có:
AB là đường vuông góc kẻ từ A đến BC
AC là đường xiên kẻ từ A đến BC
=> AC > AB
Từ (*) và (**) => Giá trị của đoạn AM lớn nhất bằng đoạn AC
Điều đó xảy ra khi điểm M trùng với điểm C
Vậy AM lớn nhất khi M trùng C
Giải Toán 7 tập 2 bài 32 trang 65
Bài 9.6 trang 65 Toán 7 tập 2
Chiều cao của tam giác ứng với một cạnh của nó có phải khoảng cách từ đỉnh đối diện đến đường thẳng chứa cạnh đó không?
Hướng dẫn giải:
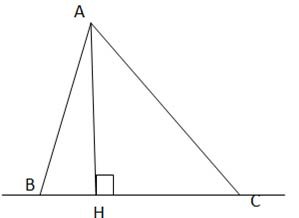
Dựa theo hình thì AH chính là chiều cao của tam giác ABC. AH ⊥ BC và AH là đoạn ngắn nhất so với AB và AC nên AH chính là khoảng cách từ a đến đoạn thẳng BC.
Bài 9.7 trang 65 Toán 7 tập 2
Cho hình vuông ABCD. Hỏi trong 4 đỉnh của hình vuông
a) Đỉnh nào cách đều hai điểm A và C
b) Đỉnh nào cách đều hai đường thẳng AB và AD
Hướng dẫn giải:

a) Đỉnh B và đỉnh D
b) Đỉnh C
Bài 9.8 trang 65 Toán 7 tập 2
Cho tam giác cân ABc, AB=AC. Lấy điểm M tùy ý nằm giữa B và C (H.9.12)
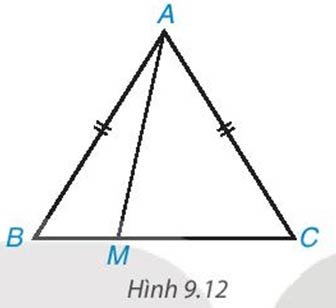
a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M đê độ dài AM nhỏ nhất
b) Chứng minh răng với mọi điểm M thì AM<AB
Hướng dẫn giải:
a)
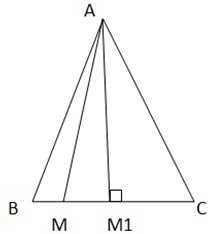
Gọi M1 là trung điểm của cạnh đáy BC. Suy ra AM1 ⊥ BC. AM1 chính là khoảng cách từ A đến BC
Theo định lí về đường xiên và đường vuông góc thì AM1 chính là đường ngắn nhất trong tam giác ABC
Vậy nếu M là trung điểm của BC thì AM sẽ có độ dài nhỏ nhất
b) Khi M nằm giữa C và B
Nếu BM < MC thì ta sẽ được góc tù $\widehat{AMB}$ . Theo định lý về góc và cạnh đối diện, AB sẽ lớn hơn AM
Tương tự khi BM>MC. ta sẽ được góc tù$\widehat{AMC}$ . Theo định lý về góc và cạnh đối diện, AC sẽ lớn hơn AM
Mà AB=AC. Suy ra, bất cứ điểm nào nằm giữa B và C, AM luôn bé hơn AB.
Bài 9.9 trang 65 Toán 7 tập 2
Cho tam giác ABC vuông tại A. Hai điểm M, N theo thứ tự nằm trên các cạnh AB, AC ( M,N không phải là đỉnh của tam giác). (H.9.13). Chứng minh rằng MN < BC. Gợi ý, so sánh MN với NB, NB với BC).
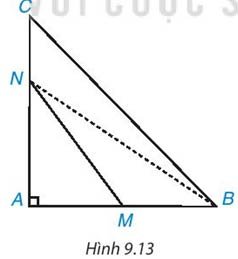
Hướng dẫn giải:
Nối N với B
NA là đường vuông góc từ điểm N xuống đoạn AN và AB
NB là đường xiên, AB là hình chiếu của NB. NM là hình xiên, AM là hình chiếu của NM
AM < AB=> NM < NB
Tương tự, AC là hình chiếu của đường xiên BC, AN là hình chiếu của đường xiên NB
AN< AC=> NB<BC
Từ đó ta thấy NM<BC
