Giải Toán 7 tập 2 bài 36: Hình hộp chữ nhật và hình lập phương
Giải Toán 7 tập 2 bài 36: Hình hộp chữ nhật và hình lập phương
Giải toán 7 tập 2 bài 36 sách Kết nối tri thức có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 7 Kết nối tri thức mới. Mời các em học sinh cùng quý phụ huynh tham khảo.
Giải Toán 7 tập 2 bài 36 trang 86
HĐ1 trang 86 Toán 7 tập 2
Hình nào dưới đây là đồ vật hoặc kiến trúc có dạng hình hộp chữ nhật, có dạng hình lập phương?
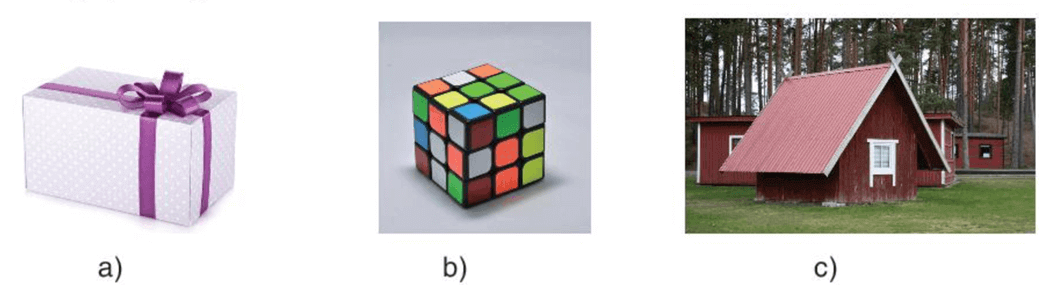
Em hãy tìm thêm một số hình ảnh có dạng hình hộp chữ nhật, hình lập phương trong thực tế.
Hướng dẫn giải:
Hộp quà ở ý a có dạng hình hộp chữ nhật.
Khối rubik ở ý b có dạng hình lập phương.
Một số hình có dạng hình hộp chữ nhật: hộp bút, quyển sách, căn phòng …
Hình có dạng hình lập phương: con xúc xắc …
HĐ2 trang 86 Toán 7 tập 2
Quan sát Hình 10.1.
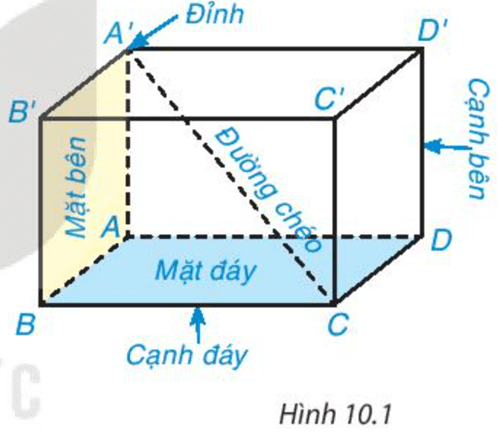
a) Nêu tên các đỉnh, cạnh, đường chéo của hình hộp chữ nhật ABCD.A’B’C’D’.
Hình hộp chữ nhật có bao nhiêu đỉnh? Có bao nhiêu cạnh? Có bao nhiêu đường chéo?
b) Gọi tên các mặt bên, mặt đáy của hình hộp chữ nhật ABCD.A’B’C’D’.
Hướng dẫn giải:
a) Các đỉnh của hình hộp chữ nhật ABCD.A’B’C’D’ là: A, B, C, D, A’, B’, C’, D’.
Các cạnh của hình hộp chữ nhật ABCD.A’B’C’D’ là: AB, BC, CD, DA, A’B’, B’C’, C’D’, D’A’, AA’, BB’, CC’, DD’.
Các đường chéo của hình hộp chữ nhật ABCD.A’B’C’D’ là: A’C, B’D, C’A. D’B.
Hình hộp chữ nhật có 8 đỉnh, 12 cạnh, 4 đường chéo.
b) Các mặt bên của hình hộp chữ nhật ABCD.A’B’C’D’ là: ABB’A’, AA’D’D, CDD’C’, BCC’B’.
Các mặt đáy của hình hộp chữ nhật ABCD.A’B’C’D’ là: ABCD, A’B’C’D’.
HĐ3 trang 86 Toán 7 tập 2
Quan sát Hình 10.2 và gọi tên đỉnh, cạnh, đường chéo, mặt đáy, mặt bên của hình lập phương MNPQ.ABCD.
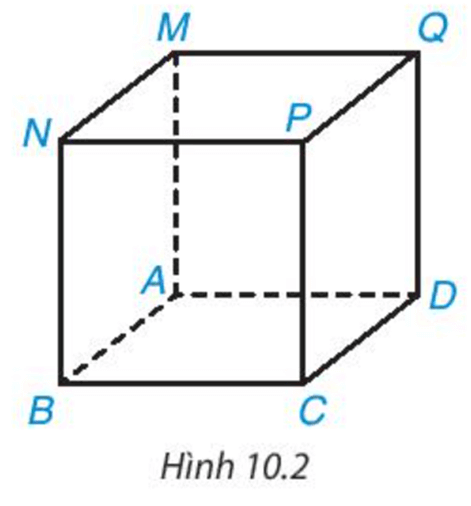
Hướng dẫn giải:
Các đỉnh của hình lập phương MNPQ.ABCD là: M, N, P, Q, A, B, C, D.
Các cạnh của hình lập phương MNPQ.ABCD là: MN, NP, PQ, QM, AB, BC, CD, DA, MA, NB, PC, QD.
Các đường chéo của hình lập phương MNPQ.ABCD là: MC, ND, PA, QB.
Các mặt đáy của hình lập phương MNPQ.ABCD là: MNPQ, ABCD.
Các mặt bên của hình lập phương MNPQ.ABCD là: MNBA, NBCP, PCDQ, MADQ.
Giải Toán 7 tập 2 bài 36 trang 87
Thực hành trang 87 Toán 7 tập 2
Sử dụng bìa cứng, cắt và gấp một chiếc hộp có dạng hình hộp chữ nhật với kích thước như Hình 10.3 theo hướng dẫn sau:
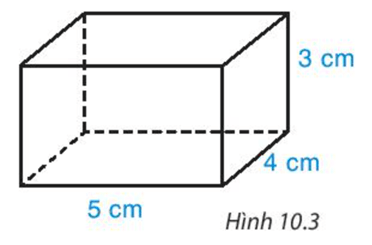
Bước 1. Vẽ hình triển khai của hình hộp chữ nhật theo kích thước đã cho như Hình 10.4.
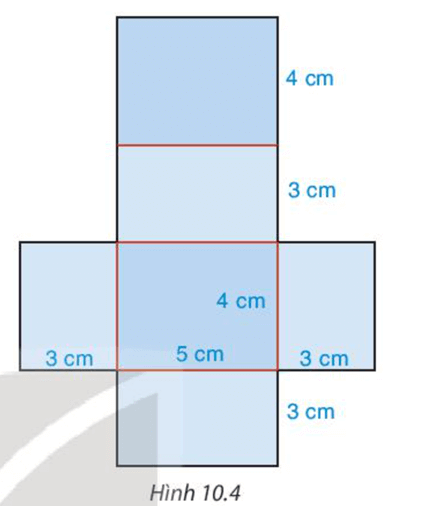
Bước 2. Cắt theo viền.
Bước 3. Gấp theo đường màu cam để được hình hộp chữ nhật (H.10.5).
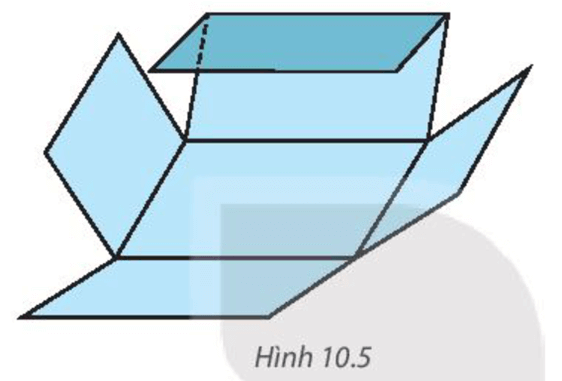
Hướng dẫn giải:
Học sinh tự thực hiện theo hướng dẫn.
Vận dụng 1 trang 87 Toán 7 tập 2
Hãy cắt và gấp hình lập phương có cạnh 4 cm.
Hướng dẫn giải:
Thực hiện theo các bước như sau:
Bước 1. Vẽ hình triển khai của hình lập phương với độ dài cạnh bằng 4 cm.
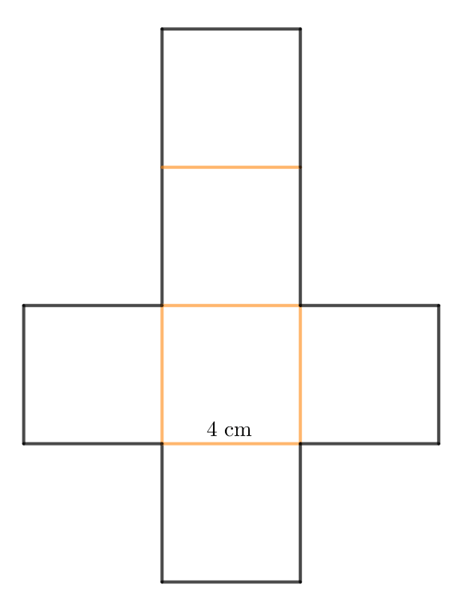
Bước 2. Cắt theo viền.
Bước 3. Gấp theo đường màu cam để được hình lập phương.
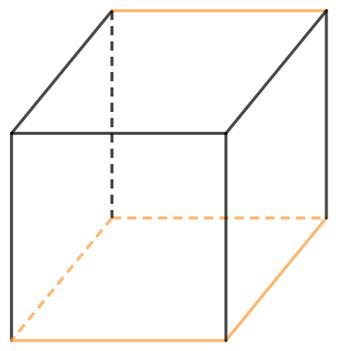
HĐ4 trang 87 Toán 7 tập 2
Quan sát hình hộp chữ nhật (H.10.6a) và hình triển khai của nó (H.10.6b). Hãy chỉ ra sự tương ứng giữa các mặt của hình hộp chữ nhật với các hình chữ nhật ở hình khai triển. Hình chữ nhật nào ở hình khai triển là các mặt bên, là các mặt đáy?
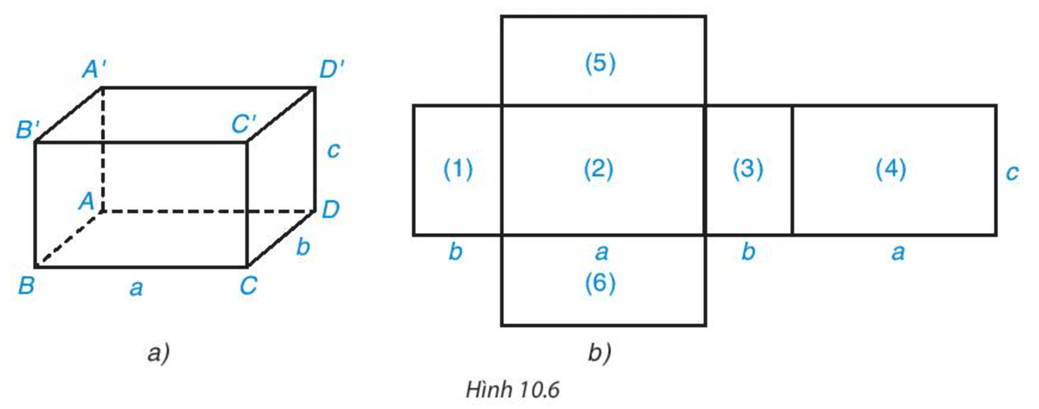
Hướng dẫn giải:
Vì hình chữ nhật (1) có cạnh là b và c nên nó có thể là mặt AA’B’B hoặc CC’D’D. Ta có thể chọn mặt đó là ABB’A’.
Hình chữ nhật (2) có cạnh là a và c nên nó có thể là mặt BB’C’C hoặc mặt AA’D’D. Ta có thể chọn mặt đó là AA’D’D.
Hình chữ nhật (3) có cạnh là b và c nên nó là mặt CC’D’D (do AA’B’B đã chọn là hình (1))
Hình chữ nhật (4) có cạnh là a và c nên nó là mặt BB’C’C (do AA’D’D đã được chọn là hình (2)).
Hình chữ nhật (5) và hình chữ nhật (6) là hai mặt còn lại ABCD và A’B’C’D. Vì hai hình chữ nhật này bằng nhau nên ta chọn hình chữ nhật (5) là A’B’C’D’ và hình chữ nhật (6) là ABCD.
Khi đó, ta có hình vẽ:
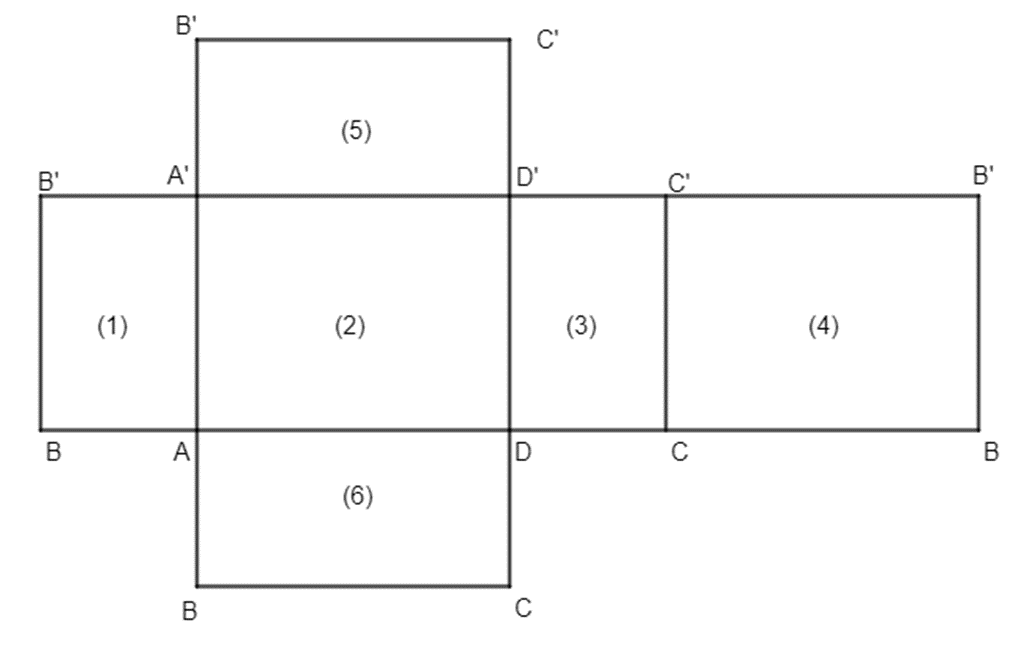
Vậy khai triển của các mặt bên là hình chữ nhật (1); (2); (3); (4).
Khi triển của các mặt đáy là (5); (6).
HĐ5 trang 87 Toán 7 tập 2
Tính tổng diện tích các hình chữ nhật (1), (2), (3), (4). So sánh kết quả vừa tìm với tích của chu vi đáy và chiều cao của hình hộp chữ nhật.
Hướng dẫn giải:
Diện tích hình (1) là bc, diện tích hình (2) là ac, diện tích hình (3) là bc, diện tích hình (4) là ac.
Khi đó tổng diện tích các hình (1), (2), (3), (4) là:
ac + bc + bc + ac = 2(ac + bc) = 2(a + b)c.
Chu vi đáy của hình hộp chữ nhật là 2(a + b).
Khi đó tích của chu vi đáy và chiều cao của hình hộp chữ nhật là 2(a + b)c.
Vậy hai kết quả vừa tìm được bằng nhau.
Giải Toán 7 tập 2 bài 36 trang 88
Luyện tập 1 trang 88 Toán 7 tập 2
Bác Tú thuê thợ sơn xung quanh bốn mặt ngoài của thành bể nước có dạng hình hộp chữ nhật có chiều dài 3 m, chiều rộng 2 m, chiều cao 1,5 m với giá 20 000 đồng/m2. Hỏi bác Tú phải trả chi phí là bao nhiêu?
Hướng dẫn giải:
Diện tích xung quanh của bể nước là: 2.(3 + 2).1,5 = 15 (m2).
Bác Tú phải trả số tiền là: 20 000 . 15 = 300 000 (đồng).
Vậy bác Tú phải trả 300 000 đồng.
Giải Toán 7 tập 2 bài 36 trang 90
Luyện tập 2 trang 90 Toán 7 tập 2
Một hình lập phương có cạnh bằng a cm, diện tích xung quanh bằng 100 cm2. Hỏi thể tích của hình lập phương đó bằng bao nhiêu?
Hướng dẫn giải:
Do hình lập phương có cạnh bằng a cm nên diện tích xung quanh của hình lập phương đó là 4a2 = 100
hay a2 = 25 do đó a = 5 cm (do a là độ dài cạnh hình lập phương nên a > 0).
Khi đó thể tích của hình lập phương đó bằng 53 = 125 (cm3).
Vậy thể tích của hình lập phương bằng 125 cm3.
Vận dụng 2 trang 90 Toán 7 tập 2
Một chiếc thùng giữ nhiệt (H.10.10) có lòng trong có dạng một hình hộp chữ nhật với chiều dài 50 cm, chiều rộng 30 cm, chiều cao 30 cm. Tính dung tích của thùng giữ nhiệt đó.

Hướng dẫn giải:
Dung tích của chiếc thùng là: 50 . 30 . 30 = 45 000 (cm3).
Đổi 45 000 cm3 = 45 dm3 = 45 l.
Vậy dung tích của thùng giữ nhiệt là 45 l.
Bài 10.1 trang 90 Toán 7 tập 2
Có bao nhiêu hình lập phương nhỏ trong Hình 10.11?
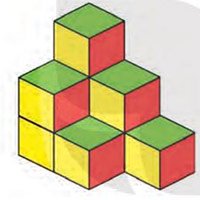
Hướng dẫn giải:
Có tất cả 9 hình lập phương nhỏ.
Bài 10.2 trang 90 Toán 7 tập 2
Gọi tên các đỉnh, cạnh, đường chéo, mặt của hình hộp chữ nhật trong Hình 10.12.
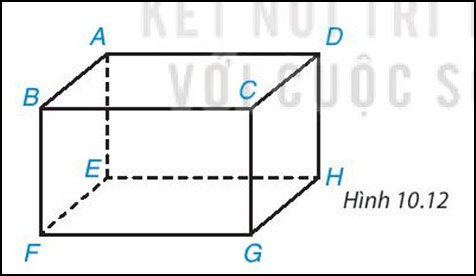
Hướng dẫn giải:
Ta gọi tên như sau:
- 8 đỉnh: A, B, C, D, E, F, G, H.
- 12 cạnh: AB, AD, DC, BC, EF, EH, FG, GH, AE, B F, CG, DH
- 4 đường chéo: AG, CE, BH, DF
- 8 mặt: ABFE, DCGH, BCGF, ADHE, ABCD, EFGH.
Bài 10.3 trang 90 Toán 7 tập 2
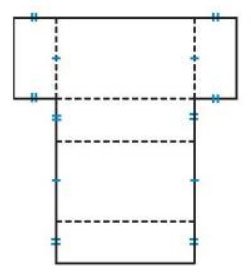
Vẽ lên một tấm bìa hình khai triển của hình hộp chữ nhật (tương tự hình bên) với kích thước tùy chọn. Cắt rời hình đã vẽ rồi gấp theo đường nét đứt để được một hình hộp chữ nhật.
Giải Toán 7 tập 2 bài 36 trang 91
Bài 10.4 trang 91 Toán 7 tập 2
Một xe đông lạnh có thùng hàng dạng hình hộp chữ nhật, kích thước lòng thùng hàng dài 5,6m, rộng 2m, cao 2m. Tính thể tích lòng của thùng hàng.
Hướng dẫn giải:
Thể tích của lòng thùng hàng là:
5,6.2.2 = 22,4 (m3)
Bài 10.5 trang 91 Toán 7 tập 2
Một hộp sữa tươi có dạng hình hộp chữ nhật với dung tích 1 lít, chiều cao 20cm, chiều dài 10cm.
a) Tính chiều rộng của hộp sữa.
b) Tính diện tích vật liệu dùng để làm vỏ hộp sữa? (coi như phần mép hộp không đáng kể)

Hướng dẫn giải:
Dung tích của hộp sữa là 1 lít, nên thể tích của hộp sữa cũng là 1 lít
Đổi: 1 lít = 1000cm3
a) Chiều rộng của hộp sữa là:
1000: (20 x 10) = 1000 : 200= 5 (cm)
b) Diện tích vật liệu dùng để làm vỏ hộp sữa là diện tích xung quanh và diện tích của hai mặt đáy của hình hộp.
Diện tích xung quanh của hộp sữa là:
2.20.(10 + 5 ) + 2. = 600 (cm2)
Diện tích của hai mặt đáy là:
2.10.5 = 100 (cm2)
Vậy diện tích vật liệu cần dùng là: 600 + 100 = 700 (cm2).
Bài 10.6 trang 91 Toán 7 tập 2
Một bể nước có dạng hình hộp chữ nhật với chiều dài 2m. Lúc đầu bể không có nước. Sau khi đổ vào bể 120 thùng nước, mỗi thùng chứa 20 lít nước thì mực nước của bể dâng cao 0,8 m
a) Tính chiều rộng của bể nước.
b) Người ta đổ thêm 60 thùng nước nữa thì đầy bể. Hỏi bể cao bao nhiêu mét?
Hướng dẫn giải:
a) Thể tích nước đổ vào:
120 x 20 = 2400 (l) = 2,4 (m3)
Chiều rộng của bể nước:
2,4 : (2 x 0,8) = 1,5 (m)
b) Thể tích của bể nước:
2400 + (60 x 20) = 3600 (l) = 3,6 (m3)
Chiều cao của bể nước:
3,6 : (2 x 1,5) = 1,2 (m)
