Luyện tập chung

Giải toán 7 tập 2 trang 45: Luyện tập chung sách Kết nối tri thức có đáp án chi tiết cho từng bài tập trong sách giáo khoa Toán lớp 7 Kết nối tri thức mới. Mời các em học sinh cùng quý phụ huynh tham khảo.

Giải Toán 7 tập 2 trang 45

Bài 7.36 trang 45 Toán 7 tập 2

Rút gọn biểu thức sau:

(5x³ – 4x²) : 2x² + (3x⁴ + 6x) : 3x – x(x² – 1)

Lời giải:

(5x³ – 4x²) : 2x² + (3x⁴ + 6x) : 3x – x(x² – 1)

= 5x³ : 2x² + (-4x²) : 2x² + 3x⁴ : 3x + 6x : 3x + (-x) . x² + (-x) . (-1)

= (5 : 2) . (x³ : x²) + (-4 : 2) . (x² : x²) + (3 : 3) . (x⁴ : x) + (6 : 3) . (x : x) + (-x³) + x

= 2,5x + (-2) + x³ + 2 – x³ + x

= (x³ – x³) + (2,5x + x) + (-2 + 2)

= 3,5x.

Bài 7.37 trang 45 Toán 7 tập 2

Rút gọn các biểu thức sau:

a) 2x(x+3) – 3x²(x+2) + x(3x² + 4x – 6)

b) 3x(2x² – x) – 2x²(3x+1) + 5(x² – 1)

Hướng dẫn giải:

a) 2x(x+3) – 3x²(x+2) + x(3x² + 4x – 6)

= (2x . x + 2x . 3) – (3x² . x + 3x² . 2) + (x . 3x² + x . 4x – x . 6)

= 2x² + 6x – (3x³ + 6x²) + (3x³ + 4x² – 6x)

= 2x² + 6x – 3x³ – 6x² + 3x³ + 4x² – 6x

= (– 3x³ + 3x³ ) + (2x² – 6x² + 4x² ) + (6x – 6x)

= 0 + 0 + 0

= 0

b) 3x(2x² – x) – 2x²(3x+1) + 5(x² – 1)

= [3x . 2x² + 3x . (-x)] – (2x² . 3x + 2x² . 1) + [5x² + 5 . (-1)]

= 6x³ – 3x² – (6x³ +2x²) + 5x² – 5

= 6x³ – 3x² – 6x³ – 2x² + 5x² – 5

= (6x³ – 6x³ ) + (-3x² – 2x² + 5x²) – 5

= 0 + 0 – 5

= – 5

Bài 7.38 trang 45 Toán 7 tập 2

Tìm giá trị của x biết rằng:

a) 3x² – 3x(x – 2) = 36

b) 5x(4x² – 2x + 1) – 2x(10x² – 5x + 2) = -36

Hướng dẫn giải:

a) 3x² – 3x(x – 2) = 36

3x² – (3x . x – 3x . 2) = 36

3x² – (3x² – 6x) = 36

3x² – 3x² + 6x = 36

6x = 36

x = 36 : 6

x = 6

Vậy x = 6.

b) 5x(4x² – 2x + 1) – 2x(10x² – 5x + 2) = -36

(5x . 4x² – 5x . 2x + 5x . 1) – (2x . 10x² – 2x . 5x + 2x . 2) = –36

(20x³ – 10x² + 5x) – (20x³ – 10x² + 4x) = –36

20x³ – 10x² + 5x – 20x³ + 10x² – 4x = –36

(20x³ – 20x³) + (-10x² + 10x²) + (5x – 4x) = -36

x = -36

Vậy x = -36.

Bài 7.39 trang 45 Toán 7 Tập 2

Thực hiện các phép tính sau:

a) (x³ – 8) : (x – 2);

b) (x – 1)(x + 1)(x² + 1).

Lời giải:

a) Đặt tính chia như sau:

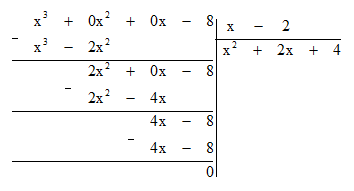
Vậy (x³ – 8) : (x – 2) = x² + 2x + 4.

b) (x – 1)(x + 1)(x² + 1)

= [x . (x + 1) + (-1) . x + (-1) . 1] . (x² + 1)

= [x . x + x . 1 + (-1) . x + (-1) . 1] . (x² + 1)

= (x² + x – x – 1)(x² + 1)

= (x² – 1)(x² + 1)

= x² . x² + x² . 1 + (-1) . x² + (-1) . 1

= x⁴ + x² – x² – 1

= x⁴ – 1

Vậy (x – 1)(x + 1)(x² + 1) = x⁴ – 1.

Bài 7.40 trang 45 Toán 7 Tập 2

Trong một trò chơi ở câu lạc bộ Toán học, chủ trò viết lên bảng biểu thức:

P(x) = x²(7x – 5) – (28x⁵ – 20x⁴ – 12x³) : 4x².

Luật chơi là sau khi chủ trò đọc một số a nào đó, các đội chơi phải tính giá trị của P(x) tại x = a. Đội nào tính đúng và tính nhanh nhất thì thắng cuộc.

Khi chủ trò vừa đọc a = 5, Vuông đã tính ngay được P(a) = 15 và thắng cuộc. Em có biết Vuông làm cách nào không?

Lời giải:

P(x) = x²(7x – 5) – (28x⁵ – 20x⁴ – 12x³) : 4x²

= x² . 7x + x² . (-5) -[28x⁵ : 4x² + (-20x⁴) : 4x² + (-12x³) : 4x²]

= 7x³ – 5x² – [7x³ – 5x² – 3x]

= 7x³ – 5x² – 7x³ + 5x² + 3x

= (7x³ – 7x³) + (-5x² + 5x²) + 3x

= 3x.

Ta thấy kết quả thu gọn đa thức P(x) = 3x.

Do đó với x = a = 5 thì bạn Vuông đã gấp 3 lần số a được P(5) = 3 . 5 = 15.

Bài 7.41 trang 45 Toán 7 Tập 2

Tìm số b sao cho đa thức x³ – 3x² + 2x – b chia hết cho đa thức x – 3.

Lời giải:

Đặt đặt tính chia như sau:

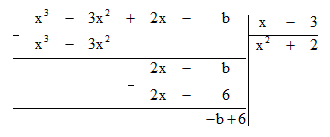
Để đa thức x³ – 3x² + 2x – b chia hết cho đa thức x – 3 thì số dư phải bằng 0

Tức là, -b + 6 = 0

Do đó b = 6.

Vậy b = 6.