Toán 10 tập 1 trang 77 Bài 2: Giải tam giác. Tính diện tích tam giác

Giải toán 10 tập 1 trang 77 Cánh diều bài 2 có đáp án chi tiết cho từng bài tập trong sách giáo khoa toán lớp 10 tập 1 Cánh diều. Mời các em học sinh cùng quý phụ huynh tham khảo.

Toán 10 tập 1 trang 77

Bài 1 trang 77 Toán 10 tập 1 Cánh diều

Cho tam giác ABC có BC = 12,CA = $15,\widehat C = {120^o}$.

Tính:

a) Độ dài cạnh AB.

b) Số đo các góc A, B.

c) Diện tích tam giác ABC.

Lời giải

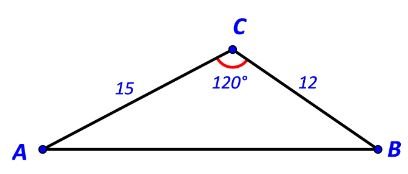
a) Áp dụng định lí cosin trong tam giác ABC ta có:

$A{B^2} = A{C^2} + B{C^2} – 2.AC.BC.\cos C$

$\begin{array}{l} \Leftrightarrow A{B^2} = {15^2} + {12^2} – 2.15.12.\cos {120^o}\\ \Leftrightarrow A{B^2} = 549\\ \Leftrightarrow AB \approx 23,43\end{array}$

b) Áp dụng định lí sin trong tam giác ABC, ta có:

$\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}$

$\Rightarrow \sin A = \frac{{BC}}{{AB}}.\sin C = \frac{{12}}{{23,43}}.\sin {120^o} \approx 0,44$

$\Rightarrow \widehat A \approx {26^o}$ hoặc $\widehat A \approx {154^o}$ (Loại)

Khi đó: $\widehat B = {180^o} – ({26^0} + {120^0 }) = {34^0}$

c)

Diện tích tam giác ABC là: $S = \frac{1}{2}CA.CB.\sin C = \frac{1}{2}.15.12.\sin {120^o} = 45\sqrt 3$

Bà 2 trang 77 Toán 10 tập 1 Cánh diều

Cho tam giác ABC có $AB = 5,BC = 7,\widehat A = {120^o}$ . Tính độ dài cạnh AC.

Lời giải

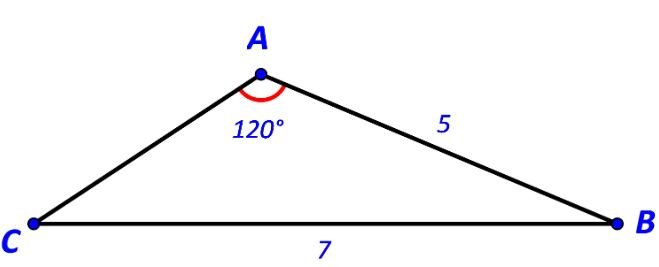
Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}}$

$\Rightarrow \sin C = \sin A.\frac{{AB}}{{BC}} = \sin {120^o}.\frac{5}{7} = \frac{{5\sqrt 3 }}{{14}}$

$\Rightarrow \widehat C \approx 38,{2^o}$ hoặc $\widehat C \approx 141,{8^o}$ (Loại)

Ta có: $\widehat A = {120^o},\widehat C = 38,{2^o} \Rightarrow \widehat B = {180^o} – \left( {{{120}^o} + 38,{2^o}} \right) = 21,{8^o}$

Áp dụng định lí cosin trong tam giác ABC ta có:

$\begin{array}{l}A{C^2} = A{B^2} + B{C^2} – 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {5^2} + {7^2} – 2.5.7.\cos 21,{8^o}\\ \Rightarrow A{C^2} \approx 9\\ \Rightarrow AC = 3\end{array}$

Vậy độ dài cạnh AC là 3.

Bài 3 trang 77 Toán 10 tập 1 Cánh diều

Cho tam giác ABC có $AB = 100,\widehat B = {100^o},\widehat C = {45^o}$

. Tính:

a) Độ dài các cạnh AC, BC

b) Diện tích tam giác ABC.

Lời giải

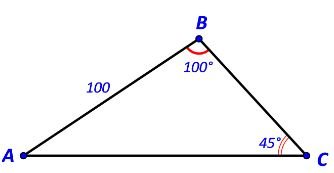
a)

Ta có: $\widehat A = {180^o} – (\widehat B + \widehat C) \Rightarrow \widehat A = {180^o} – ({100^o} + {45^o}) = {35^o}$

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}$

$\Rightarrow \left\{ \begin{array}{l}AC = \sin B.\frac{{AB}}{{\sin C}}\\BC = \sin A.\frac{{AB}}{{\sin C}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}AC = \sin {100^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 139,3\\BC = \sin {35^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 81,1\end{array} \right.$

b)

Diện tích tam giác ABC là: $S = \frac{1}{2}.BC.AC.\sin C = \frac{1}{2}.81,1.139,3.\sin {45^o} \approx 3994,2.$

Bài 4 trang 77 Toán 10 tập 1 Cánh diều

Cho tam giác ABC có AB = 12,AC = 15,BC = 20.

Tính:

a) Số đo các góc A, B, C.

b) Diện tích tam giác ABC.

Lời giải

a) Áp dụng định lí cosin trong tam giác ABC, ta có:

$\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}};\;\cos B = \frac{{{a^2} + {c^2} – {b^2}}}{{2ac}}$

Thay a = BC = 20;b = AC = 15;c = AB = 12.

$\Rightarrow \cos A = – \frac{{31}}{{360}};\;\cos B = \frac{{319}}{{480}}$

$\Rightarrow \widehat A = 94,{9^o};\;\widehat B = 48,{3^o}$

$\Rightarrow \widehat C = {180^o} – \left( {94,{9^o} + 48,{3^o}} \right) = 36,{8^o}$

b)

Diện tích tam giác ABC là: S = $\frac{1}{2}.bc.\sin A = \frac{1}{2}.15.12.\sin 94,{9^o} \approx 89,7.$

Bài 5 trang 77 Toán 10 tập 1 Cánh diều

Tính độ dài cạnh AB trong mỗi trường hợp sau:

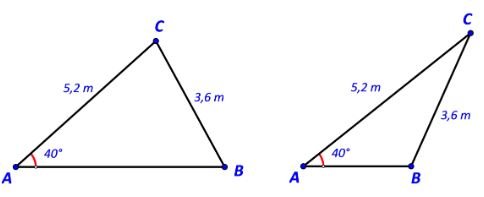
Lời giải

Áp dụng định lí sin trong tam giác ABC, ta có:

$\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}}$

$\Rightarrow \sin B = \frac{{AC.\sin A}}{{BC}} = \frac{{5,2.\sin {{40}^o}}}{{3,6}} \approx 0,93$

$\Rightarrow \widehat B \approx 68,{2^o}$ hoặc $\widehat B \approx 111,{8^o}$

Trường hợp 1: $\widehat B \approx 68,{2^o}$

Ta có: $\widehat C = {180^o} – (\widehat A + \widehat B) = {180^o} – ({40^o} + 68,{2^o}) = 71,{8^o}$

Áp dụng định lí sin trong tam giác ABC, ta có:

$\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}$

$\Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin 71,{8^o}.\frac{{3,6}}{{\sin {{40}^o}}} \approx 5,32$

Trường hợp 2: $\widehat B \approx 111,{8^o}$

Ta có: $\widehat C = {180^o} – (\widehat A + \widehat B) = {180^o} – ({40^o} + 111,{8^o}) = 28,{2^o}$

Áp dụng định lí sin trong tam giác ABC, ta có:

$\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}}$

$\Rightarrow AB = \sin C.\frac{{BC}}{{\sin A}} = \sin 28,{2^o}.\frac{{3,6}}{{\sin {{40}^o}}} \approx 2,65$

Vậy AB = 5,32 hoặc AB = 2,65.

Bài 6 trang 77

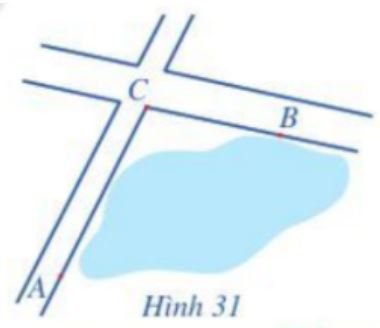
Để tính khoảng cách giữa hai địa điểm A và B mà ta không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …), người ta tiến hành như sau: Chọn một địa điểm C sao cho ta đo được các khoảng cách AC, CB và góc ACB. Sau khi đo, ta nhận được: AC = 1 km, CB = 800 m và $\widehat {ACB} = {105^o}$

(Hình 31). Tính khoảng cách AB (làm tròn kết quả đến hàng phần mười đơn vị mét).

Lời giải

Đổi: 1 km = 1000 m. Do đó AC = 1000 m.

Áp dụng định lí cosin trong tam giác ABC ta có:

$A{B^2} = A{C^2} + B{C^2} – 2.AC.BC.\cos C$

$\begin{array}{l} \Rightarrow A{B^2} = {1000^2} + {800^2} – 2.1000.800.\cos {105^o}\\ \Rightarrow A{B^2} \approx 2054110,5\\ \Rightarrow AB \approx 1433,2\end{array}$

Vậy khoảng cách AB là 1433,2 m.

Bài 7 trang 77

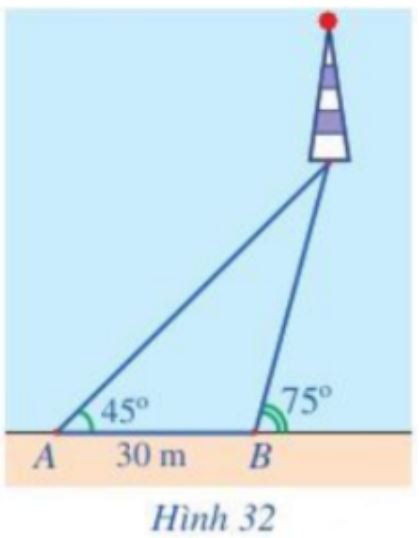
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 45⁰ và 75⁰ . Biết khoảng cách giữa hai vị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

Lời giải

Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB.

Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.

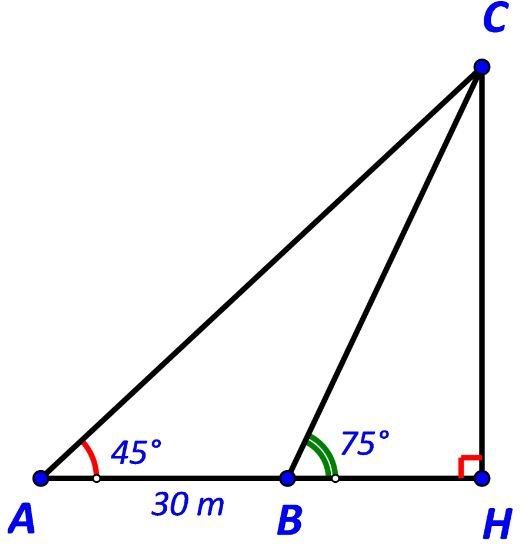
Ta có:

$\widehat {ACB} = \widehat {HBC} – \widehat {BAC} = {75^o} – {45^o} = {30^o}; \, \widehat {ABC} = {180^o} – {75^o} = {105^o}$

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}$

$\Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^o}.\frac{{30}}{{\sin {{30}^o}}} \approx 58$

Tam giác ACH vuông tại H nên ta có:

CH = $\sin A.AC = \sin {45^o}.58 \approx 41$

Vậy ngọn hải đăng cách bờ biển 41 m.