Toán 10 tập 1 trang 82 Bài 3: Khái niệm vectơ

Giải toán 10 tập 1 trang 82 Cánh diều bài 3 có đáp án chi tiết cho từng bài tập trong sách giáo khoa toán lớp 10 tập 1 Cánh diều. Mời các em học sinh cùng quý phụ huynh tham khảo.

Toán 10 tập 1 trang 82

Bài 1 trang 82 Toán 10 tập 1 Cánh diều

Cho A, B, C là ba điểm thẳng hàng, B nằm giữa A và C. Viết các cặp vectơ cùng hướng, ngược hướng trong những vectơ sau: $\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {BA} ,\overrightarrow {BC} ,\overrightarrow {CA} ,\overrightarrow {CB} .$

Lời giải

Do các vectơ đều nằm trên đường thẳng AB nên các vectơ này đều cùng phương với nhau.

Dễ thấy:

Các vectơ $\overrightarrow {AB}$ ,$\overrightarrow {AC}$ ,$\overrightarrow {BC}$ cùng hướng (từ trái sang phải.)

Các vectơ $\overrightarrow {BA}$ ,$\overrightarrow {CA}$ ,$\overrightarrow {CB}$ cùng hướng (từ phải sang trái.)

Do đó, các cặp vectơ cùng hướng là:

$\overrightarrow {AB}$ và $\overrightarrow {AC}$

$\overrightarrow {AC}$ và $\overrightarrow {BC}$

$\overrightarrow {AB}$ và $\overrightarrow {BC}$

$\overrightarrow {BA}$ và $\overrightarrow {CA}$

$\overrightarrow {BA}$ và $\overrightarrow {CB}$

$\overrightarrow {BA}$ và $\overrightarrow {CB}$

Các cặp vectơ ngược hướng là:

$\overrightarrow {AB}$ và $\overrightarrow {BA}$

$\overrightarrow {AB}$ và $\overrightarrow {CA}$

$\overrightarrow {AB}$ và $\overrightarrow {CB}$

$\overrightarrow {AC}$ và $\overrightarrow {BA}$

$\overrightarrow {AC}$ và $\overrightarrow {CA}$ ;

$\overrightarrow {AC}$ và $\overrightarrow {CB}$

$\overrightarrow {BC}$ và $\overrightarrow {BA}$ ;

$\overrightarrow {BC}$ và $\overrightarrow {CA}$

$\overrightarrow {BC}$ và $\overrightarrow {CB}$

Bài 2 trang 82 Toán 10 tập 1 Cánh diều

Cho đoạn thẳng MN có trung điểm là I.

a) Viết các vectơ khác vectơ-không có điểm đầu, điểm cuối là một trong ba điểm M, N, I.

b) vectơ nào bằng $\overrightarrow {MI}$ ? Bằng $\overrightarrow {NI}$ ?

Lời giải

a) Các vectơ đó là: $\overrightarrow {MI} ,\overrightarrow {IM} ,\overrightarrow {IN} ,\overrightarrow {NI} ,\overrightarrow {MN} ,\overrightarrow {NM}$ .

b) Dễ thấy:

+) $vectơ \overrightarrow {IN}$ cùng hướng với vectơ $\overrightarrow {MI}$

. Hơn nữa: $|\overrightarrow {IN} |\; = IN = MI = \;|\overrightarrow {MI} |$

$\Rightarrow \overrightarrow {IN} = \overrightarrow {MI}$

+) vectơ $\overrightarrow {IM}$ cùng hướng với vectơ $\overrightarrow {NI}$

. Hơn nữa:$|\overrightarrow {IM} |\; = IM = NI = \;|\overrightarrow {NI} |$

$\Rightarrow \overrightarrow {IM} = \overrightarrow {NI}$

Vậy $\overrightarrow {IN}$ = $\overrightarrow {MI}$ và $\overrightarrow {IM} = \overrightarrow {NI}$ .

Bài 3 trang 82 Toán 10 tập 1 Cánh diều

Cho hình thang ABCD có hai đáy là AB và . Tìm vectơ:

a) Cùng hướng với $\overrightarrow {AB}$

b) Ngược hướng với $\overrightarrow {AB}$

Lời giải

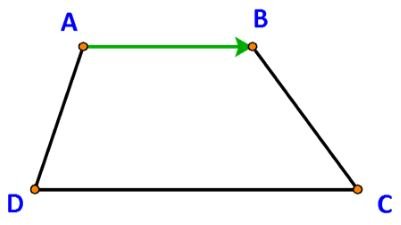
Giá của vectơ $\overrightarrow {AB}$ là đường thẳng AB.

Các vectơ cùng phương với vectơ $\overrightarrow {AB}$ là:$ \overrightarrow {CD}$ và $\overrightarrow {DC}$

a) vectơ $\overrightarrow {DC}$ cùng hướng với vectơ $\overrightarrow {AB}$ .

b) vectơ $\overrightarrow {CD}$ ngược hướng với vectơ $\overrightarrow {AB}$

Bài 4 trang 82 Toán 10 tập 1 Cánh diều

Cho hình vuông ABCD có độ dài cạnh bằng 3cm. Tính độ dài của các vectơ $\overrightarrow {AB}$ ,$\overrightarrow {AC}$ .

Lời giải

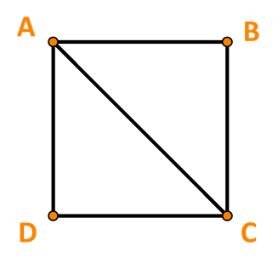
Ta có: $|\overrightarrow {AB} $| = AB và $|\overrightarrow {AC} |\ = AC.$

Mà AB = 3;AC = $3\sqrt 2$

$\Rightarrow \;|\overrightarrow {AB} |\, = 3;\;\;|\overrightarrow {AC} |\ = 3\sqrt 2$

Bài 5 trang 82 Toán 10 tập 1 Cánh diều

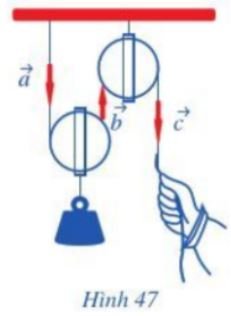
Quan sát ròng rọc hoạt động khi dùng lực để kéo một đầu của ròng rọc. Chuyển động của các đoạn dây được mô tả bằng các vectơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c$ (Hình 47).

a) Hãy chỉ ra các cặp vectơ cùng phương.

b) Trong các cặp vectơ đó, cho biết chúng cùng hướng hay ngược hướng.

Lời giải

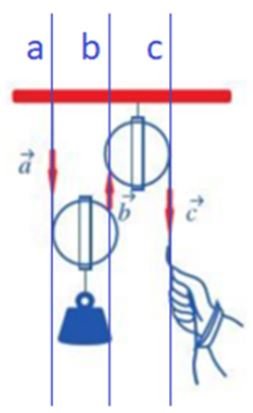
Gọi a, b, c là các đường thẳng lần lượt chứa các vectơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c$ .

Khi đó: a, b, c lần lượt là giá của các vectơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c$

a) Dễ thấy: a // b // c

$\Rightarrow$

Ba vectơ $\overrightarrow a ,\overrightarrow b ,\overrightarrow c$ cùng phương với nhau.

Vậy các cặp vectơ cùng phương là: $\overrightarrow a$ và $\overrightarrow b$, $\overrightarrow a$ và \overrightarrow c , $\overrightarrow b$ và $\overrightarrow c$.

b) Quan sát ba vectơ, ta thấy: vectơ $\overrightarrow a$ và $\overrightarrow c$ cùng hướng xuống còn vectơ $\overrightarrow b$ hướng lên trên.

Vậy vectơ $\overrightarrow a$ và $\overrightarrow c$ cùng hướng, vectơ $\overrightarrow a$ và $\overrightarrow c$ ngược hướng, vectơ $\overrightarrow b$ và $\overrightarrow c$ ngược hướng.