Toán lớp 10 tập 1 trang 22 Bài 3: Bất phương trình bậc nhất hai ẩn

Giải  toán lớp 10 tập 1 trang 22 bài 3 có đáp án chi tiết cho từng bài tập trong sách giáo khoa toán lớp 10 tập 1 Kết nối tri thức. Mời các em học sinh cùng quý phụ huynh tham khảo.

Toán lớp 10 tập 1 trang 22

Mở đầu trang 22 Toán lớp 10 tập 1 Kết nối tri thức 

Nhân ngày Quốc tế Thiếu nhi 1 – 6, một rạp chiếu phim phục vụ các khán giả của một bộ phim hoạt hình. Vé được bán ra có hai loại:

Loại 1 (dành cho trẻ từ 6 – 13 tuổi): 50 000 đồng/vé;

Loại 2 (dành cho người trên 13 tuổi): 100 000 đồng/vé.

Người ta tính toán rằng, để không phải bù lỗ thì số tiền vé thu được ở rạp chiếu phim này phải đạt tối thiểu 20 triệu đồng. Hỏi số lượng vé bán được trong những trường hợp nào thì rạp chiếu phim phải bù lỗ?

Hướng dẫn:

Sau khi học xong bài này ta có thể giải quyết bài toàn như sau:

Gọi số vé loại 1 bán được là x (vé) (x∈N∗∈ℕ*).

Gọi số vé loại 2 bán được là y (vé) (y∈N∗∈ℕ*)

Tổng số tiền bán vé thu được là 50 000x + 100 000y

Vì nếu số tiền đạt tối thiểu 20 000 000 đồng thì rạp chiếu phim không phải bù lỗ nên trường hợp rạp chiếu phim phải bù lỗ khi số tiền vé bán được nhỏ hơn 20 000 000 đồng.

Do đó, 50 000x + 100 000y < 20 000 000.

Vậy với mỗi x; y vé thỏa mãn bất phương trình trên thì rạp phim phải bù lỗ.

1. Bất phương trình bậc nhất hai ẩn

HOạT ĐộNG 1 trang 22 Toán lớp 10 tập 1 Kết nối tri thức 

Trong tình huống mở đầu, gọi x là số vé loại 1 bán được và y là số vé loại 2 bán được. Viết biểu thức tính số tiền bán vé thu được (đơn vị nghìn đồng) ở rạp chiếu phim đó theo x và y.

a) Các số nguyên không âm x và y thỏa mãn điều kiện gì để số tiền bán vé thu được đạt tối thiểu 20 triệu đồng?

b) Nếu số tiền bán vé thu được nhỏ hơn 20 triệu đồng thì x và y thỏa mãn điều kiện gì?

Hướng dẫn:

Gọi số vé loại 1 bán được là x (vé) (x∈N*).

Gọi số vé loại 2 bán được là y (vé) (y∈N∗)

Tổng số tiền bán vé thu được là 50x + 100y (nghìn đồng).

a) Để số tiền bán vé đạt tối thiểu 20 triệu đồng (20 000 nghìn đồng) thì x; y phải thỏa mãn:

50x + 100y ≥≥20 000.

b) Nếu số vé bán được nhỏ hơn 20 triệu đồng (20 000 nghìn đồng) thì x; y phải thỏa mãn điều kiện:

50x + 100y < 20 000.

Toán lớp 10 tập 1 trang 23

HOạT ĐộNG 2 trang 23 Toán lớp 10 tập 1 Kết nối tri thức 

Cặp số (x; y) = (100; 100) thỏa mãn bất phương trình bậc nhất hai ẩn nào trong hai bất phương trình thu được ở HOạT ĐộNG1? Từ đó cho biết rạp chiếu phim có phải bù lỗ hay không nếu bán được 100 vé loại 1 và 100 vé loại 2.

Trả lời câu hỏi tương tự với cặp số (x; y) = (150; 150).

Hướng dẫn:

+ Thay x = 100; y = 100 vào biểu thức tính tiền 50x + 100y ta được:

50 . 100 + 100 . 100 = 15 000 (nghìn đồng)

Vì 15 000 < 20 000 nên x = 100; y = 100 thỏa mãn bất phương trình 50x + 100y < 20 000 và không thỏa mãn bất phương trình 50x + 100y ≥≥20 000.

Vậy nếu rạp chiều phim chỉ bán được 100 vé loại 1 và 100 vé loại 2 thì rạp chiếu phim phải bù lỗ.

+ Thay x = 150; y = 150 vào biểu thức tính tiền 50x + 100y ta được:

50 . 150 + 100 . 150 = 22 500 (nghìn đồng)

Vì 22 500 > 20 000 nên x = 150; y = 150 thỏa mãn bất phương trình 50x + 100y ≥≥ 20 000 và không thỏa mãn mãn bất phương trình 50x + 100y < 20 000.

Nếu rạp chiếu phim bán được 150 vé loại 1 và 150 vé loại 2 thì rạp chiếu phim không phải bù lỗ.

Luyện tập 1 trang 23 Toán lớp 10 tập 1 Kết nối tri thức 

Cho bất phương trình bậc nhất hai ẩn x + 2y ≥ 0.

a) Hãy chỉ ra ít nhất hai nghiệm của bất phương trình trên.

b) Với y = 0, có bao nhiêu giá trị của x thỏa mãn bất phương trình đã cho?

Hướng dẫn:

a) Xét x = 0 và y = 0 ta được:

0 + 2.0 ≥0⇔0≥0 (luôn đúng)

Vậy (0; 0) là một nghiệm của bất phương trình đã cho.

Xét x = 1; y = 2 ta được:

1 + 2.2 ≥0⇔5≥0≥0 (luôn đúng)

Vậy (1; 2) là một nghiệm của bất phương trình đã cho.

b) Với y = 0 thay vào bất phương trình ta được:

x + 2.0 ≥0⇔x≥0

Vậy với giá trị y = 0 có vô số giá trị x thỏa mãn bất phương trình sao cho x≥ 0x≥ 0.

2. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn trên mặt phẳng tọa độ

HOạT ĐộNG 3 trang 23 Toán lớp 10 tập 1 Kết nối tri thức 

Cho đường thẳng d: 2x – y = 4 trên mặt phẳng tọa độ Oxy (H.2.1). Đường thẳng này chia mặt phẳng thành hai nửa mặt phẳng.

a) Các điểm O(0; 0), A(-1; 3) và B(-2; -2) có thuộc cùng một nửa mặt phẳng bờ là đường thẳng d không?

Tính giá trị của biểu thức 2x – y tại các điểm đó và so sánh với 4.

b) Trả lời câu hỏi tương tự như câu a với các điểm C(3; 1), D(4; – 1).

Hướng dẫn:

a) Quát sát hình vẽ ta thấy O; A; B thuộc cùng một nửa mặt phẳng bờ là đường thẳng d.

+ Thay tọa độ điểm O(0; 0) vào biểu thức 2x – y ta được:

2.0 – 0 = 0 < 4.

+ Thay tọa độ điểm A(-1; 3) vào biểu thức 2x – y ta được:

2.(-1) – 3 = -5 < 4.

+ Thay tọa độ điểm B(-2; -2) vào biểu thức 2x – y ta được:

2.(-2) – (-2) = -2 < 4.

b) Quát sát hình vẽ ta thấy C; D thuộc cùng một nửa mặt phẳng bờ là đường thẳng d.

+ Thay tọa độ điểm C(3; 1) vào biểu thức 2x – y ta được:

2.3 – 1 = 5 > 4.

+ Thay tọa độ điểm D(4; -1) vào biểu thức 2x – y ta được:

2.4 + 1 = 9 > 4.

Toán lớp 10 tập 1 trang 24

Luyện tập 2 trang 24 Toán lớp 10 tập 1 Kết nối tri thức

Biểu diễn miền nghiệm của bất phương trình 2x + y < 200 trên mặt phẳng tọa độ.

Hướng dẫn:

Bước 1: Vẽ đường thẳng d: 2x + y – 200 = 0 trên mặt phẳng tọa độ.

Bước 2: Lấy điểm O(0; 0) không thuộc đường thẳng d.

Thay x = 0, y = 0 vào 2x + y ta được: 2.0 + 0 = 0 < 200.

Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d có chứa điểm O (miền tô màu không chứa đường thẳng d).

Toán lớp 10 tập 1 trang 25

Vận dụng trang 25 Toán lớp 10 tập 1 Kết nối tri thức

Một công ty viễn thông tính phí 1 nghìn đồng mỗi phút gọi nội mạng và 2 nghìn đồng mỗi phút gọi ngoại mạng. Em có thể sử dụng bao nhiêu phút gọi nội mạng và bao nhiêu phút gọi ngoại mạng trong một tháng nếu em muốn số tiền phải trả ít hơn 200 nghìn đồng?

Hướng dẫn:

Gọi số phút gọi nội mạng em sử dụng là x; số phút gọi ngoại mạng em sử dụng là y (x; y ≥ 0).y (x; y ≥ 0).

Khi đó số tiền phải trả cho số phút gọi nội mạng là x (nghìn đồng); số tiền phải trả cho số phút gọi ngoại mạng là 2y (nghìn đồng).

Tổng số tiền phải trả cho x phút gọi nội mạng và y phút gọi ngoại mạng là: x + 2y (nghìn đồng)

Để số tiền phải trả ít hơn 200 nghìn đồng thì x; y phải thỏa mãn bất phương trình:

x + 2y < 200.

Do đó, muốn số tiền trả ít hơn 200 nghìn đồng thì số phút gọi nội mạng và số phút gọi ngoại mạng y phải là nghiệm của bất phương trình x + 2y < 200.

Chẳng hạn với x = 50, y = 50 thì x + 2y = 50 + 2 . 50 = 150 < 200, do đó cặp số (50; 50) thỏa mãn bất phương trình x + 2y < 200 nên nếu gọi 50 phút nội mạng và 50 phút ngoại mạng thì số tiền phải trả sẽ ít hơn 200 nghìn đồng.

Bài 2.1 trang 25 Toán lớp 10 tập 1 Kết nối tri thức

Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?

a) 2x + 3y > 6;

b) 2²x + y ≤ 0;

c) 2x² – y ≥ 1.

Hướng dẫn:

a) 2x + 3y > 6 là bất phương trình bậc nhất hai ẩn vì nó có dạng ax + by > c.với a, b không đồng thời bằng 0.

b) 2²x + y ≤ 0⇔4x + y ≤ 0 là bất phương trình bậc nhất hai ẩn vì nó có dạng ax + by ≤ c, với a, b không đồng thời bằng 0.

c) 2x² – y ≥ 1 không là bất phương trình bậc nhất hai ẩn vì nó có x² (ẩn x với bậc là 2) với hệ số khác 0.

Bài 2.2 trang 25 Toán lớp 10 tập 1 Kết nối tri thức

Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng tọa độ:

a) 3x + 2y ≥ 300;

b) 7x + 20y < 0.

Hướng dẫn:

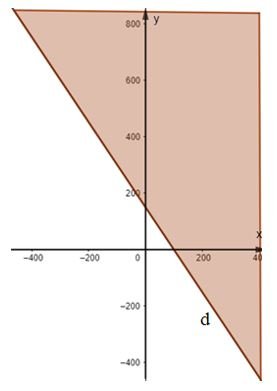
a)

Vẽ đường thẳng d: 3x + 2y – 300 = 0 trên mặt phẳng tọa độ.

Lấy gốc tọa độ O(0; 0) và tính 3.0 + 2.0 = 0 < 300.

Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d không chứa gốc tọa độ và cả đường thẳng d (miền tô màu kể cả biên).

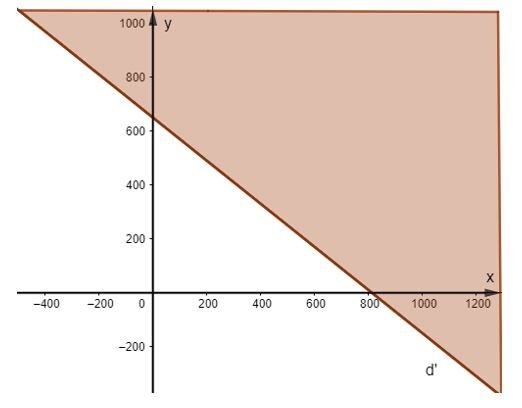
b)

Vẽ đường thẳng d’: 7x + 20y = 0 trên mặt phẳng tọa độ.

Lấy điểm M (200; 200) và tính 7.200 + 20.200 = 5400 > 0.

Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d’ không chứa điểm M và không chứa đường thẳng d’ (miền tô màu không kể biên).

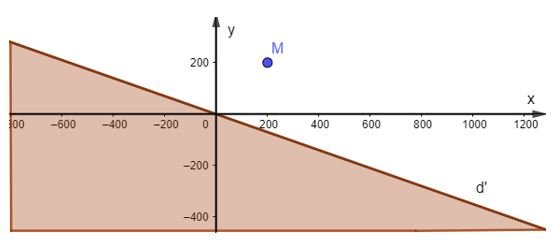
Bài 2.3 trang 25 Toán lớp 10 tập 1 Kết nối tri thức

Ông An muốn thuê một chiếc ô tô (có lái xe) trong một tuần. Giá thuê xe được cho như bảng sau:

a) Gọi x và y lần lượt là số kilômét ông An đi trong các ngày từ thứ Hai đến thứ Sáu và trong hai ngày cuối tuần. Viết bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng.

b) Biểu diễn miền nghiệm của bất phương trình ở câu a trên mặt phẳng tọa độ.

Hướng dẫn:

a) Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Hai đến thứ Sáu là:

900.5 + 8x = 4 500 + 8x (nghìn đồng).

Số tiền ông An phải trả cho việc thuê xe ô tô từ thứ Hai đến thứ Sáu là:

1 500.2 + 10y = 3 000 + 10y (nghìn đồng).

Tổng số tiền ông An phải trả cho việc thuê xe trong một tuần là:

4 500 + 8x + 3 000 + 10y = 7 500 + 8x + 10y (nghìn đồng).

Để tổng số tiền ông An phải trả không quá 14 triệu đồng thì

7 500 + 8x + 10y ≤ 14 000

⇔ 8x + 10y ≤ 6 500.

⇔ 4x + 5y ≤ 3 250.

Vậy bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng là 4x + 5y ≤ 3 250.

b)

Vẽ đường thẳng d: 4x + 5y = 3 250 trên mặt phẳng tọa độ.

Lấy gốc tọa độ O(0; 0) và tính 4.0 + 5.0 = 0 < 3 250.

Do đó miền nghiệm của bất phương trình là nửa mặt phẳng có bờ là đường thẳng d kchứa gốc tọa độ và cả đường thẳng d (miền không tô màu kể cả biên).