Bài 5: Giá trị lượng giác của một góc từ 0 độ đến 180 độ

Giải  toán lớp 10 tập 1 trang 37 bài 5 có đáp án chi tiết cho từng bài tập trong sách giáo khoa toán lớp 10 tập 1 Kết nối tri thức. Mời các em học sinh cùng quý phụ huynh tham khảo.

Toán lớp 10 tập 1 trang 37

Bài 3.1 trang 37

Không dùng bảng số hay máy tính cầm tay, tính giá trị các biểu thức sau:

a) (2sin30⁰ + cos135⁰ – 3tan150⁰).(cos180⁰ – cos60⁰);

b) sin²90⁰ + cos²120⁰ + cos²0⁰ – tan²60⁰ + cos²135⁰;

c) cos60⁰.sin30⁰ + cos²30⁰.

Hướng dẫn:

a) (2sin30⁰ + cos135⁰ – 3tan150⁰).(cos180⁰ – cos60⁰)

= (2sin30⁰ – cos45⁰ + 3tan30⁰).(-1 – tan30⁰)

=$(2\frac12-\frac{\sqrt2}2+3\frac{\sqrt3}3)(-1-\frac{\sqrt3}3)=\;(1-\frac{\sqrt2}2+\sqrt3)(\frac{-1-\sqrt3}{\sqrt3})3,194$

b) sin²90⁰ + cos²120⁰ + cos²0⁰ – tan²60⁰ + cot²135⁰

= sin²90⁰ + cos²120⁰ + cos²0⁰ – tan²60⁰ + cot²45⁰

$=\;1+\;{(\frac12)}^2\;+1-{(\sqrt3)}^2+1$

$=\;1+\frac14+1-3+1=\frac14$

c) cos60⁰.sin30⁰ + cos²30⁰

$=\;\frac12.\frac12+\left(\frac{\sqrt3}2\right)^2$

$=\;\frac14+\frac34=\frac44=1$

Bài 3.2 trang 37

Đơn giản các biểu thức sau:

a) sin100⁰ + sin80⁰ + cos16⁰ + cos 164⁰;

b) 2sin(180⁰ – α)cotα – cos(180⁰ – α).tanα.cos(180⁰ – α) với 0⁰ < α < 90⁰.

Hướng dẫn:

a) sin100⁰ + sin80⁰ + cos16⁰ + cos 164⁰

= sin100⁰ + sin100⁰ + cos 164⁰ + cos 164⁰

= 2sin100⁰ + 2cos 164⁰.

b) 2sin(180⁰ – α)cotα – cos(180⁰ – α).tanα.cos(180⁰ – α) với 0⁰ < α < 90⁰

=2sinαcotα−cosα.tanα.cotα

$=\;2\;\sin\;\alpha\;\frac{\cos\alpha}{\sin\alpha}-\cos\alpha.\frac{\sin\alpha}{\cos\alpha}.\frac{\cos\alpha}{\sin\alpha}$

=2cosα−cosα=cosα

Bài 3.3 trang 37

Chứng minh các hệ thức sau:

a) sin²α + cos²α = 1;

b) $1\;+\;\tan^2\alpha\;=\;\frac1{\cos^2\alpha}\;(\alpha\;\neq\;90^0)$

c) $1\;+\;cot^2\alpha\;=\;\frac1{\sin^2\alpha}(\;0^0<\;\alpha\;<\;180^0)\;.$

Hướng dẫn:

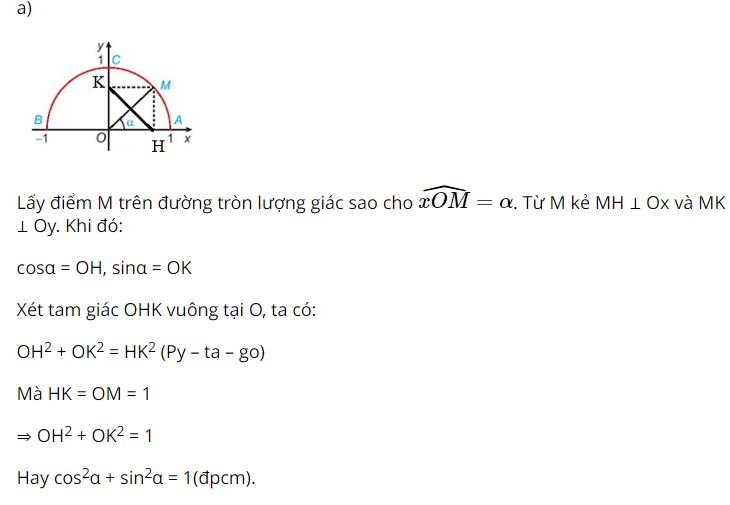
b) Ta có:

$\begin{aligned}& 1+\tan ^2 \alpha=1+\left(\frac{\sin \alpha}{\cos \alpha}\right)^2=1+\frac{\sin ^2 \alpha}{\cos ^2 \alpha} \\& =\frac{\cos ^2 \alpha+\sin ^2 \alpha}{\cos ^2 \alpha}=\frac{1}{\cos ^2 \alpha}\left(\alpha \neq 90^0\right)\end{aligned}$

c) Ta có:

$\begin{aligned}& 1+\cot ^2 \alpha=1+\left(\frac{\cos \alpha}{\sin \alpha}\right)^2=1+\frac{\cos ^2 \alpha}{\sin ^2 \alpha} \\& =\frac{\cos ^2 \alpha+\sin ^2 \alpha}{\sin ^2 \alpha}=\frac{1}{\sin ^2 \alpha}\left(0^0<\alpha<180^0\right)\end{aligned}$

Bài 3.4 trang 37

Cho góc α ( 00 < α < 1800) thỏa mãn α = 3.

Tính giá trị của biểu thức:

$P\;=\frac{2\;\sin\;\alpha\;-\;3\;cos\;\alpha}{3\;\sin\;\alpha\;+\;2\;cos\;\alpha}$

Chia cả tử và mẫu của biểu thức P cho cosα ≠ 0 với 0⁰ < α < 180⁰ ta được:

$P\;=\;\frac{2.{\displaystyle\frac{\sin\alpha}{cos\;\alpha}}-3}{3.{\displaystyle\frac{\sin\alpha}{cos\;\alpha}}+2}=\frac{2\;\tan\;\alpha\;-\;33\;\tan\;\alpha\;+\;}{3\;\tan\;\alpha\;+\;2}=\;\frac{2.3\;-\;3}{3.3\;+\;2}=\frac3{11}$

Vậy với α (0₀ < α < 180⁰) thỏa mãn tanα = 3 thì P=$\frac{3}{11}$