Toán lớp 10 tập 1 trang 44: Bài tập cuối chương 3
Toán lớp 10 tập 1 trang 44: Bài tập cuối chương 3
Giải toán lớp 10 tập 1 trang 44 bài tập cuối chương 3 có đáp án chi tiết cho từng bài tập trong sách giáo khoa toán lớp 10 tập 1 Kết nối tri thức. Mời các em học sinh cùng quý phụ huynh tham khảo.
Toán lớp 10 tập 1 trang 44
Bài 3.12 trang 44 Toán lớp 10 tập 1 Kết nối tri thức
Cho tam giác ABC có $\widehat B = {135^0}$
. Khẳng định nào sau đây đúng?
a)
A. $S = \frac{1}{2}ca$
B. $S = \frac{{ – \sqrt 2 }}{4}ac$
C. S = $\frac{{\sqrt 2 }}{4}bc$
D. S = $\frac{{\sqrt 2 }}{4}ca$
b)
A. $R = \frac{a}{{\sin A}}$
B. $R = \frac{{\sqrt 2 }}{2}b$
C. R = $\frac{{\sqrt 2 }}{2}c$
D. R = $\frac{{\sqrt 2 }}{2}a$
c)
A. ${a^2} = {b^2} + {c^2} + \sqrt 2 ab$
B. $\frac{b}{{\sin A}} = \frac{a}{{\sin B}}$
C. $\sin B = \frac{{ – \sqrt 2 }}{2}$
D. ${b^2} = {c^2} + {a^2} – 2ca.\cos {135^0}$
Hướng dẫn:
a) Đáp án D
b) Đáp án B
c) Đáp án D
Bài 3.13 trang 44 Toán lớp 10 tập 1 Kết nối tri thức
Cho tam giác ABC. Khẳng định nào sau đây là đúng?
a)
A. S = $\frac{{abc}}{{4r}}$ B. r = $\frac{{2S}}{{a + b + c}}$
| C. a2= b2+ c2 + 2bc . cosA | D. S = r . (a + b + c) |
b)
| A. sinA = sin(B + C) | B. cosA = cos(B + C) |
| C. cosA > 0 | D. sinA ≤ 0 |
Hướng dẫn:
a) S = pr = $\frac{{abc}}{{4R}} = \frac{{\left( {a + b + c} \right).r}}{2}$
=> Đáp án A và D là đáp án sai
Theo định lí cos, ta có: a2 = b2 + c2 – 2bc.cosA. Do đó C sai.
Ta có:
S = $\frac{{\left( {a + b + c} \right).r}}{2} \Rightarrow r = \frac{{2S}}{{a + b + c}}$
=> Đáp án B là đáp án đúng
b)
Ta có: $\widehat A + \widehat B + \widehat C = {180^0} \Rightarrow \widehat A = {180^0} – \left( {\widehat B + \widehat C} \right)$
$\sin \widehat A = \sin \left[ {{{180}^0} – \left( {\widehat B + \widehat C} \right)} \right] = \sin \left( {\widehat B + \widehat C} \right)$
=> Đáp án A đúng
$\cos \widehat A = \cos \left[ {{{180}^0} – \left( {\widehat B + \widehat C} \right)} \right] = – \cos \left( {\widehat B + \widehat C} \right)$
=> Đáp án B sai
Ta có: $\cos A > 0$
khi ${0^0} < \widehat A < {90^0}$
=> Đáp án C sai
Trong một tam giác ta có: ${0^0} \leqslant \widehat A \leqslant {180^0}$
=> sin A ≥ 0
=> Đáp án D đúng
Chọn đáp án A
Bài 3.14 trang 44 Toán lớp 10 tập 1 Kết nối tri thức
Tính giá trị các biểu thức sau:
a) M = sin450.cos450+ sin300;
b) N = $\sin {60^0}.\cos {30^0} + \frac{1}{2}\sin {45^0}.\cos {45^0}$
c) P = 1 + tan2600;
d) Q = $\frac{1}{{2{{\sin }^2}{{120}^0} – \cot {{120}^0}}}$
Hướng dẫn:
a) M = sin450.cos450+ sin300
$= \frac{{\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2} + \frac{1}{2} = \frac{1}{2} + \frac{1}{2} = 1$
b) $N = \sin {60^0}.\cos {30^0} + \frac{1}{2}\sin {45^0}.\cos {45^0}$
$\frac{{\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{2} + \frac{1}{2}.\frac{{\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2} = \frac{3}{4} + \frac{1}{4} = 1$
c) P = 1 + tan2600
$= 1 + {\left( {\sqrt 3 } \right)^2} = 1 + 3 = 4$
d) $Q = \frac{1}{{2{{\sin }^2}{{120}^0} – \cot {{120}^0}}}$
= $\frac{1}{{{{\sin }^2}60}} + \cot {60^0} = \frac{4}{3} + \frac{1}{{\sqrt 3 }} = \frac{{4 + \sqrt 3 }}{3}$
Bài 3.15 trang 44 Toán lớp 10 tập 1 Kết nối tri thức
Cho tam giác ABC có $\widehat B = {60^0};\widehat C = {45^0}$, AC = 10. Tính a, R, S.r.
Hướng dẫn:
Hình vẽ minh họa:

Xét tam giác ABC ta có:
$\hat A = {180^0} – \hat B – \hat C = {180^0} – {60^0} – {45^0} = {75^0}$
$\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R$
$\Rightarrow \frac{{\text{a}}}{{\sin {\text{A}}}} = \frac{{\text{b}}}{{\sin {\text{B}}}} = \frac{{10}}{{\sin {{60}^0}}} = \frac{{10}}{{\dfrac{{\sqrt 3 }}{2}}} = \frac{{20}}{{\sqrt 3 }}$
$\Rightarrow {\text{a}} = \frac{{20}}{{\sqrt 3 }}\sin {\text{A}} = \frac{{20}}{{\sqrt 3 }}.\sin {75^0} = 11,15$
$\Rightarrow 2{\text{R}} = \frac{{\text{b}}}{{\sin {\text{B}}}} = \frac{{20}}{{\sqrt 3 }} \Leftrightarrow {\text{R}} = \frac{{10}}{{\sqrt 3 }}$
Diện tích tam giác ABC là:
$S = \frac{1}{2}.b.a.\sin C = \frac{1}{2}.10.11,15.\sin {45^0} \approx 39,42$
$\Rightarrow \frac{c}{{\sin C}} = \frac{b}{{\sin B}} = \frac{{20}}{{\sqrt 3 }} \Rightarrow c = \frac{{20}}{{\sqrt 3 }}.\sin C = \frac{{20}}{{\sqrt 3 }}.\sin {45^0} = \frac{{10\sqrt 6 }}{3}$
Ta có:
$S = p.r = \frac{{\left( {a + b + c} \right).r}}{2} \Rightarrow r = \frac{{2S}}{{a + b + c}} = 2,69$
Bài 3.16 trang 44 Toán lớp 10 tập 1 Kết nối tri thức
Cho tam giác ABC có trung tuyến AM. Chứng minh rằng:
a) $\cos \widehat {AMB} + \cos \widehat {AMC} = 0$
b) $M{A^2} + M{B^2} – A{B^2} = 2MA.MB.\cos \widehat {AMB}$ và $M{A^2} + M{C^2} – A{C^2} = 2MA.MC.\cos \widehat {AMC}$
c) $M{A^2} = \frac{{2\left( {A{B^2} + A{C^2}} \right) – B{C^2}}}{4}$(Công thức đường trung tuyến)
Hướng dẫn:

a) $\cos \widehat {AMB} + \cos \widehat {AMC} = 0$
Ta có: $\widehat {AMB} + \widehat {AMC} = {180^0} \Rightarrow \widehat {AMC} = {180^0} – \widehat {AMB}$
=> $\cos \widehat {AMB} = – \cos \left( {{{180}^0} – \widehat {AMB}} \right) = – \cos \widehat {AMC}$
=> $\cos \widehat {AMB} + \cos \widehat {AMC} = 0$
=> Điều phải chứng minh
b) $M{A^2} + M{B^2} – A{B^2} = 2MA.MB.\cos \widehat {AMB}$ và $M{A^2} + M{C^2} – A{C^2} = 2MA.MC.\cos \widehat {AMC}$
Xét tam giác ABM ta có:
AB2 = MA2 + MB2 – 2MA.MB.cosAMB
=> MA2 + MB2 – AB2 = 2MA.MB.cosAMB (1)
Xét tam giác AMC, ta có:
AC2 = MA2 + MC2 – 2MA.MC.cosAMC
=> MA2 + MC2 – AC2 = 2MA.MC.cosAMC (2)
c) $M{A^2} = \frac{{2\left( {A{B^2} + A{C^2}} \right) – B{C^2}}}{4}$ (Công thức đường trung tuyến)
Cộng vế với vế của (1) với (2), ta được:
MA2 + MB2 – AB2 + MA2 + MC2 – AC2 = 2MA.MB.cosAMB + 2MA.MC.cosAMC
$\begin{matrix}2M{A^2}+\frac{{B{C^2}}}{4}-A{B^2}+\frac{{B{C^2}}}{4}-A{C^2}\\=2MA\cdot\frac{{BC}}{2}\cdot\cos\widehat{AMB}+2MA\cdot\frac{{BC}}{2}\cdot\cos\widehat{AMC}{\text{(}}MB=MC=\frac{{BC}}{2}{\text{)}}\\\end{matrix}$
$\begin{matrix}\Leftrightarrow 2{\text{M}}{{\text{A}}^2}+\frac{{{\text{B}}{{\text{C}}^2}}}{2}-{\text{A}}{{\text{B}}^2}-{\text{A}}{{\text{C}}^2}=2{\text{MA}}{\text{.}}\frac{{{\text{BC}}}}{2}.(\cos\widehat{{\text{AMB}}}+\cos\widehat{{\text{AMC}}})\\\Leftrightarrow 2{\text{M}}{{\text{A}}^2}+\frac{{{\text{B}}{{\text{C}}^2}}}{2}-{\text{A}}{{\text{B}}^2}-{\text{A}}{{\text{C}}^2}=0(\cos\widehat{{\text{AMB}}}+\cos\widehat{{\text{AMC}}}=0)\Leftrightarrow 2{\text{M}}{{\text{A}}^2}=\frac{{2{\text{A}}{{\text{B}}^2}+2{\text{A}}{{\text{C}}^2}-{\text{B}}{{\text{C}}^2}}}{2}\\\end{matrix}$
=> $M{A^2} = \frac{{2\left( {A{B^2} + A{C^2}} \right) – B{C^2}}}{4}$
Bài 3.17 trang 44 Toán 10 tập 1 Kết nối tri thức
Cho tam giác ABC. Chứng minh rằng:
a) Nếu góc A nhọn thì b2 + c2 > a2;
b) Nếu góc A tù thì b2 + c2 < a2;
c) Nếu góc A vuông thì b2 + c2 = a2.
Hướng dẫn:
Xét tam giác ABC ta có:
Theo định lí cos, ta có: a2 = b2 + c2 – 2bc . cosA
a) Nếu góc A nhọn thì cosA > 0 ⇒ 2bc cosA > 0 ⇒ – 2bc cosA < 0
=> a2 = b2 + c2 – 2bc . cosA < b2 + c2
Vậy b2 + c2 > a2
b) Nếu góc A tù thì cosA > 0 ⇒ 2bccosA < 0 ⇒ – 2bc cosA > 0
=> a2 = b2 + c2 – 2bc . cosA > b2 + c2
Vậy b2 + c2 < a2.
c) Nếu góc A vuông thì cosA = 0 ⇒ 2bc cosA = 0
=> a2 = b2 + c2 – 2bc . cosA = b2 + c2
Vậy b2 + c2 = a2
Bài 3.18 trang 44 Toán 10 tập 1 Kết nối tri thức
Trên biển, tàu B ở vị trí cách tàu A 53 km về hương N340E. Sau đó, tàu B chuyển động thẳng đều với vận tốc có độ lớn 30km/h về hướng đông và tàu A chuyển động thẳng đều với vận tốc có độ lớn 50km/h để đuổi kịp tàu B.
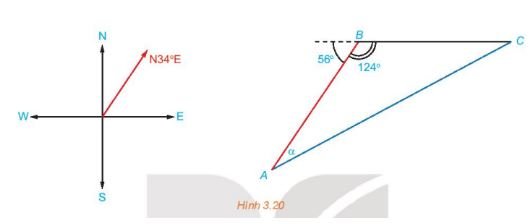
a) Hỏi tàu A cần phải chuyển động theo hướng nào?
b) Với hướng chuyển động đó thì sau bao lâu tàu A đuổi kịp tàu B?
Hướng dẫn:
a) Gọi thời gian tàu A đuổi kịp tàu B ở vị trí C là x (giờ) (x > 0)
Vì tàu B chuyển động thẳng đều với vận tốc có độ lớn 30km/h đến C nên quãng đường BC là 30x (km)
Vì tàu A chuyển động thẳng đều với vận tốc có độ lớn 50km/h để đuổi kịp tàu B nên quãng đường AC là 50x (km)
Xét tam giác ABC ta có:
AC2 = BC2 + AB2 – 2AB . BC . cosB
=> 2500x2 = 900x2 + 532 – 2 . 53 . 30x . cos1240
=> 1600x2 – 1778x – 2809 = 0
$\left[{\begin{array}{*{20}{c}}{x\approx 1,99\left({tm}\right)}\\{x\approx-0,88\left({ktm}\right)}\end{array}}\right.$
Do đó tàu A mất 1,99 giờ đuổi kịp tàu B.
=> BC = 30 . x = 30 . 1,99 = 59,7; AC = 50 . x = 50 . 1,99 = 99,5
Ta lại có:
$\begin{matrix}\dfrac{{BC}}{{\sin A}}=\dfrac{{AC}}{{\sin B}}\Rightarrow\dfrac{{59,7}}{{\sin A}}=\dfrac{{99,5}}{{\sin{{124}^0}}}\\\Rightarrow\sin A\approx 0,497\Rightarrow\widehat B\approx 29,{83^0}\\\end{matrix}$
=> AC hợp với phương nam một góc 340 + 29,830 = 63,830
Vậy tàu A chuyển động theo hướng N63,830E
Bài 3.19 trang 44 Toán 10 tập 1 Kết nối tri thức
Trên sân bóng chày dành cho nam, các vị trí gôn nhà (Home plate), gôn 1 (First base), gôn 2(Second base), gôn 3 (Third base) là bốn đỉnh của một hình vuông có cạnh dài 27,4m. Vị trí đứng ném bóng (Pitcher’s mound) nằm trên đường nối gôn Nhà với gôn 2 và cách gôn nhà 18,44m. Tính các khoảng cách từ vị trí đứng ném bóng tới các gôn 1 và gôn 3.

Hướng dẫn:
Hình vẽ minh họa:
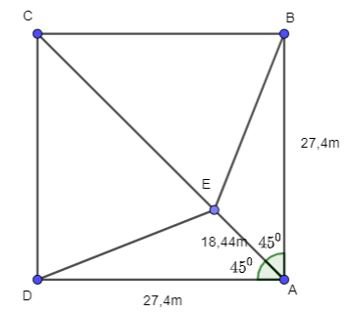
A là vị trí gôn nhà, B là vị trí gôn 1, C là vị trí gôn 2, D là vị trí gôn 3, E là vị trí ném bóng.
Xét tam giác ABE ta có:
BE2 = AB2 + AE2 – 2.AB.AE.cos
=> BE2 = 27,42 + 18,442 – 2.27,4.18,44.cos450
=> BE2 ≈ 376,25
=> BE ≈ 19,4 m.
Xét tam giác ABE và tam giác ADE ta có:
AB = AD (gt)
AE chung
$\widehat {BAE} = \widehat {DAE} = {45^0}$
=> ΔABE = ΔCDE (c – g – c)
=> BE = DE (hai cạnh tương ứng)
=> DE ≈ 19,4 m
Vậy khoảng cách từ vị trí đứng ném bóng tới các gôn 1 và gôn 3 là 19,4 m.
