Toán lớp 10 tập 1 trang 50 Bài 7: Các khái niệm mở đầu

Giải  toán lớp 10 tập 1 trang 50 bài 7 có đáp án chi tiết cho từng bài tập trong sách giáo khoa toán lớp 10 tập 1 Kết nối tri thức. Mời các em học sinh cùng quý phụ huynh tham khảo.

Toán lớp 10 tập 1 trang 50

Bài 4.1 trang 50 Toán lớp 10 tập 1 Kết nối tri thức

Cho ba vecto $\overrightarrow a ;\overrightarrow b ;\overrightarrow c$ đều khác $\overrightarrow 0$

. Những khẳng định nào sau đây đúng?

a) $\overrightarrow a ;\overrightarrow b ;\overrightarrow c$ đều cùng hướng với $\overrightarrow 0$

b) Nếu $\overrightarrow b$ không cùng hướng với $\overrightarrow a$ thì $\overrightarrow b$ ngược hướng với $\overrightarrow a$

c) Nếu $\overrightarrow a$ và $\overrightarrow b$ đều cùng phương với $\overrightarrow c$ thì \overrightarrow a và \overrightarrow b cùng phương.

d) Nếu $\overrightarrow a$ và $\overrightarrow b$ đều cùng hướng với thì $\overrightarrow a$

và $\overrightarrow b$ cùng hướng.

Hướng dẫn:

a) $\overrightarrow a ;\overrightarrow b ;\overrightarrow c$ đều cùng hướng với $\overrightarrow 0$

Mọi vecto đều cùng hướng với $\overrightarrow 0$

=> Khẳng định đúng

b) Nếu $\overrightarrow b$

không cùng hướng với $\overrightarrow a$ thì $\overrightarrow b$ ngược hướng với $\overrightarrow a$ hoặc $\overrightarrow b$ không cùng phương với $\overrightarrow a$

=> Khẳng định sai

c) Nếu $\overrightarrow a$ và $\overrightarrow b$ đều cùng phương với $\overrightarrow c$ thì $\overrightarrow a$ và $\overrightarrow b$ có giá song song hoặc trùng với $\overrightarrow c$

=> $\overrightarrow a$ và $\overrightarrow b$ có giá song song hoặc trùng nhau

=> $\overrightarrow a$ và $\overrightarrow b$ cùng phương

=> Khẳng định đúng.

d) Nếu $\overrightarrow a$ và $\overrightarrow b$ đều cùng hướng với thì $\overrightarrow a$ và $\overrightarrow b$ cùng hướng.

=> Khẳng định đúng.

Bài 4.2 trang 50 Toán lớp 10 tập 1 Kết nối tri thức

Trong hình 4.12 hãy chỉ ra các vecto cùng phương, các cặp vecto ngược hướng và các cặp vecto bằng nhau.

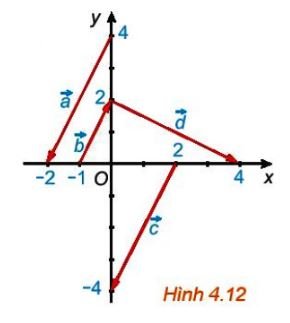
Hướng dẫn:

Quan sát hình vẽ ta thấy:

Các vecto $\overrightarrow a ;\overrightarrow b ;\overrightarrow c$ có giá song song với nhau và có cùng độ dài.

+ Các vecto cùng phương là: $\overrightarrow a ;\overrightarrow b ;\overrightarrow c$

+ Các cặp vecto ngược hướng là: $\overrightarrow a ;\overrightarrow b$ và $\overrightarrow c ;\overrightarrow b$

+ Các cặp vecto cùng hướng và bằng nhau là: $\overrightarrow a ;\overrightarrow c$

Bài 4.3 trang 50 Toán 10 tập 1 Kết nối tri thức

Chứng minh rằng tứ giác ABCD là một hình bình hành khi và chỉ khi $\overrightarrow {BC} = \overrightarrow {AD}$

Hướng dẫn:

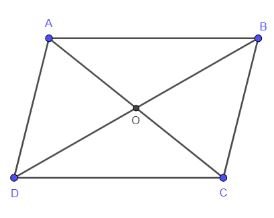
Nếu ABCD là hình bình hành => $\overrightarrow {AD} = \overrightarrow {BC}$

Chứng minh

Ta có: ABCD là hình bình hành

=> AD // BC

=> Hai vecto $\overrightarrow {AD} ;\overrightarrow {BC}$ là hai vecto cùng phương

=> Hai vecto $\overrightarrow {AD} ;\overrightarrow {BC}$ là hai vecto cùng hướng.

Mà AD = BC (tính chất hình bình hành)

=> $\overrightarrow {AD} = \overrightarrow {BC}$

Bài 4.4 trang 50 Toán 10 tập 1 Kết nối tri thức

Cho hình vuông ABCD có hai đường chéo cắt nhau tại O. Hãy chỉ ra tập hợp S gồm tất cả các vecto khác $\overrightarrow 0$ có điểm đầu và điểm cuối thuộc tập hợp {A; B; C; D; O}. Hãy chia tập S thành các nhóm sao cho hai vecto thuộc cùng một nhóm khi và chỉ khi chúng bằng nhau.

Hướng dẫn:

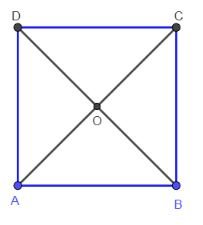
Các vecto khác $\overrightarrow 0$ có điểm đầu và điểm cuối thuộc tập hợp {A; B; C; D; O} là:

$\overrightarrow {AB} ;\overrightarrow {AC} ;\overrightarrow {AD} ;\overrightarrow {AO}$ ;

$\overrightarrow {BA} ;\overrightarrow {BC} ;\overrightarrow {BD} ;\overrightarrow {BO}$ ;

$\overrightarrow {CA} ;\overrightarrow {CB} ;\overrightarrow {CD} ;\overrightarrow {CO}$ ;

$\overrightarrow {DA} ;\overrightarrow {DB} ;\overrightarrow {DC} ;\overrightarrow {DO}$ ;

$\overrightarrow {OA} ;\overrightarrow {OB} ;\overrightarrow {OC} ;\overrightarrow {OD}$

Khi đó tập hợp cần tìm là

$S = \left\{ {\overrightarrow {AB} ;\overrightarrow {AC} ;\overrightarrow {AD} ;\overrightarrow {AO} ;\overrightarrow {BA} ;\overrightarrow {BC} ;\overrightarrow {BD} ;\overrightarrow {BO} ;\overrightarrow {CA} ;\overrightarrow {CB} ;\overrightarrow {CD} ;\overrightarrow {CO} ;\overrightarrow {DA} ;\overrightarrow {DB} ;\overrightarrow {DC} ;\overrightarrow {DO} ;\overrightarrow {OA} ;\overrightarrow {OB} ;\overrightarrow {OC} ;\overrightarrow {OD} .} \right\}$

Hai vecto bằng nhau trong tập hợp S là:

$\overrightarrow {AB} = \overrightarrow {DC} ;\overrightarrow {AD} = \overrightarrow {BC}$ ;

$\overrightarrow {BA} = \overrightarrow {CD} ;\overrightarrow {DA} = \overrightarrow {CB}$ ;

$\overrightarrow {OA} = \overrightarrow {CO} ;\overrightarrow {AO} = \overrightarrow {OC}$ ;

$\overrightarrow {DO} = \overrightarrow {OB} ;\overrightarrow {OD} = \overrightarrow {BO}$;

Khi đó tập S chia thành các nhóm là:

$\begin{matrix}\left\{{\overrightarrow{AB};\overrightarrow{DC}}\right\}\\\left\{{\overrightarrow{AD};\overrightarrow{BC}}\right\}\\\left\{{\overrightarrow{BA};\overrightarrow{CD}}\right\}\\\left\{{\overrightarrow{DA};\overrightarrow{CB}}\right\}\\\end{matrix}$

$\begin{matrix}\left\{{\overrightarrow{OA};\overrightarrow{CO}}\right\}\\\left\{{\overrightarrow{AO};\overrightarrow{OC}}\right\}\\\left\{{\overrightarrow{DO};\overrightarrow{OB}}\right\}\\\left\{{\overrightarrow{OD};\overrightarrow{BO}}\right\}\\\end{matrix}$

Bài 4.5 trang 50 Toán 10 tập 1 Kết nối tri thức

Trên mặt phẳng tọa độ Oxy, hãy vẽ vecto $\overrightarrow {OA} ;\overrightarrow {MN}$ với a(1; 2), m(0; -1), n(3; 5).

a) Chỉ ra mối quan hệ giữa hai vecto trên.

b) Một vật thể khởi hành từ M và chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu diễn bởi vecto $\overrightarrow v = \overrightarrow {OA}$

. Hỏi vật thể đó có đi qua điểm N hay không? Nếu có thì sau bao lâu vật sẽ tới N?

Hướng dẫn:

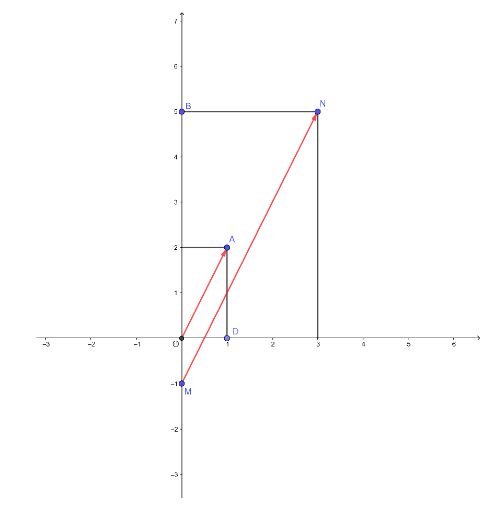
a) Quan sát hình vẽ ta thấy;

Hai vecto $\overrightarrow {OA} ;\overrightarrow {MN}$ là hai vecto cùng hướng

b) Xét tam giác OAD vuông tạị D ta có:

OA² = OD² + AD²

=> OA² = 1² + 2² = 5

=> > OA = $\sqrt 5$

Xét tam giác MNB vuông tạo B ta có:

NM² = MB² + BN²

=> NM² = 6² + 3² = 45

=>  NM = $3\sqrt 5$

Ta có $\frac{{NM}}{{OA}} = \frac{{3\sqrt 5 }}{{\sqrt 5 }} = 3$

=> NM = 3OA

Do hai vecto $\overrightarrow {OA} ;\overrightarrow {MN}$ là hai vecto cùng hướng nên vật thể chuyển động thẳng đều với vận tốc được biểu diễn $\overrightarrow v = \overrightarrow {OA}$  nên vật thể đó đi qua điểm N và sau 3 giờ thì vật sẽ tới điểm N.