Toán lớp 10 tập 1 trang 54 Bài 8: Tổng và hiệu của hai vecto

Giải  toán lớp 10 tập 1 trang 54 bài 8 có đáp án chi tiết cho từng bài tập trong sách giáo khoa toán lớp 10 tập 1 Kết nối tri thức. Mời các em học sinh cùng quý phụ huynh tham khảo.

Toán lớp 10 tập 1 trang 54

Bài 4.6 trang 54 Toán lớp 10 tập 1 Kết nối tri thức

Cho bốn điểm A, B, C, D. Chứng minh rằng:

a) $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow 0$

b) $\overrightarrow {AC} – \overrightarrow {AD} = \overrightarrow {BC} – \overrightarrow {BD}$

Hướng dẫn:

a) Ta có:

$\begin{matrix}\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}\\=\left({\overrightarrow{AB}+\overrightarrow{BC}}\right)+\left({\overrightarrow{CD}+\overrightarrow{DA}}\right)\\=\overrightarrow{AC}+\overrightarrow{CA}=\overrightarrow{AA}=\overrightarrow 0\\\end{matrix}$

b) Ta có:

$\overrightarrow {AC} – \overrightarrow {AD} = \overrightarrow {DC}$ (quy tắc hiệu)

$\overrightarrow {BC} – \overrightarrow {BD} = \overrightarrow {DC}$ (quy tắc hiệu)

=> $\overrightarrow {AC} – \overrightarrow {AD} = \overrightarrow {BC} – \overrightarrow {BD}$

Bài 4.7 trang 54 Toán lớp 10 tập 1 Kết nối tri thức

Cho hình bình hành ABCD. Hãy tìm điểm M để $\overrightarrow {BM} = \overrightarrow {AB} + \overrightarrow {AD}$. Tìm mối quan hệ giữa hai vecto $\overrightarrow {CD}$ và $\overrightarrow {CM}$

Hướng dẫn:

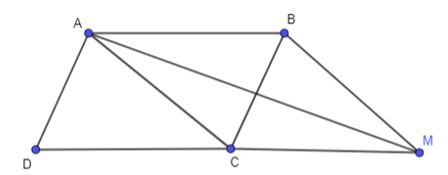
Ta có: $\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC}$ (Quy tắc hình bình hành)

Ta cần tìm điểm M thỏa mãn $\overrightarrow {AC} = \overrightarrow {BM}$=> ACMB là hình bình hành

=> $\overrightarrow {CM} = \overrightarrow {AB}$

Mà $\overrightarrow {DC} = \overrightarrow {AB}$

=> $\overrightarrow {CM} = \overrightarrow {DC}$

hay $\overrightarrow {CM} = – \overrightarrow {CD}$

Suy ra $\overrightarrow {CD} ;\overrightarrow {CM}$ là hai vecto đối nhau

Bài 4.8 trang 54 Toán lớp 10 tập 1 Kết nối tri thức

Cho tam giác đều ABC có cạnh bằng a. Tính độ dài các vecto $\overrightarrow {AB} – \overrightarrow {AC} ;\overrightarrow {AB} + \overrightarrow {AC}$

Hướng dẫn:

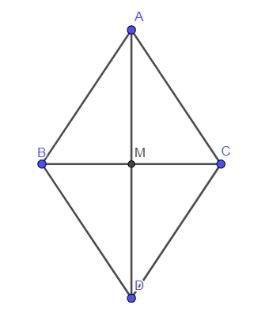
Ta có:

$\overrightarrow {AB} – \overrightarrow {AC} = \overrightarrow {CB}$ (Quy tắc hiệu)

=>$\left| {\overrightarrow {AB} – \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = a$

Ta lại có:

$\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD}$ (với D là điểm thỏa mãn ABDC là hình bình hành)

Gọi M là giao điểm của AD và BC

⇒ M là trung điểm của BC và AD (tính chất hình bình hành)

Xét tam giác ABC ta có:

AB² = AM² + BM² (định lí Py – ta – go)

=> AM² = AB² – BM²

= $A{B^2} – {\left( {\frac{{BC}}{2}} \right)^2} = {a^2} – {\left( {\frac{a}{2}} \right)^2} = \frac{{3{a^2}}}{4}$

=> AM = $\frac{{a\sqrt 3 }}{2}$

=> AD = 2AM = $2.\frac{{a\sqrt 3 }}{2} = a\sqrt 3$

=> $\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = a\sqrt 3$

Vậy $\left| {\overrightarrow {AB} – \overrightarrow {AC} } \right| = a ;\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3$

Bài 4.9 trang 54 Toán lớp 10 tập 1 Kết nối tri thức

Biểu diễn hai lực $\overrightarrow {{F_1}} ;\overrightarrow {{F_2}}$ cùng tác động lên một vật, cho $\left| {\overrightarrow {{F_1}} } \right| = 3N;\left| {\overrightarrow {{F_2}} } \right| = 2N$ . Tính độ lớn của hợp lực $\overrightarrow {{F_1}} + \overrightarrow {{F_2}}$ (hinh 4.19)

Hướng dẫn:

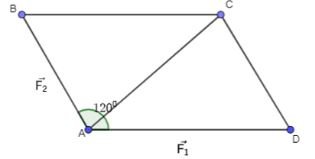
Ta có ABCD là hình bình hành

=> $\widehat {ADC} = {60^0}$

Ta có:

$\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {AD} } \right| = \left| {\overrightarrow {BC} } \right| = 3$

$\left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {DC} } \right| = 2$

$\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC}$

=> $\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {AC} } \right|$

Xét tam giác ADC ta có:

AC² = AD² + DC² – 2AD . DC . cosD

=> AC² = 3² + 2² – 2 . 3 . 2 . cos60⁰

= 7

=> AC = $\sqrt 7$

=> $\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \sqrt 7$

Bài 4.10 trang 54 Toán lớp 10 tập 1 Kết nối tri thức

Hai con tàu xuất phát cùng lúc từ bờ bên này sang bờ bên kia của dòng sông với vận tốc riêng không đổi và có độ lớn bằng nhau. Hai tàu luôn giữ được lái sao cho chúng tạo với bờ cùng một góc nhọn nhưng một tàu hướng xuống hạ lưu, một tàu hướng lên thượng nguồn (hình bên). Vận tốc dòng nước là đáng kể, các yếu tố bên ngoài khác không ảnh hưởng tới vận tốc của các tàu. Hỏi tàu nào sang bờ bên kia trước?

Hướng dẫn:

Hình vẽ

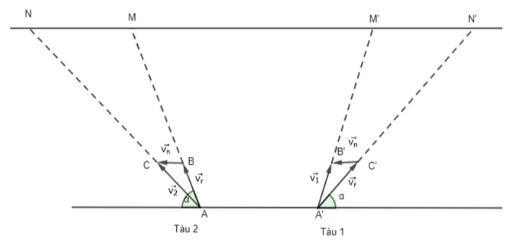
Ta biểu thị hai bờ sông là hai đường thẳng song song d₁, d₂ (H.4.17). Giả sử tàu 1 xuất phát từ A’ ∈ d₁ và bánh lái luôn được giữ để tàu tạo với bờ một góc

α. Gọi $\overrightarrow {{v_r}}$ và $\overrightarrow {{v_n}}$ lần lượt là vận tốc riêng của tàu và vận tốc dòng nước. Gọi B’, C’ là các điểm sao cho $\overrightarrow {{v_r}} = \overrightarrow {A’C’}; \overrightarrow {{v_n}} = \overrightarrow {C’B’};$

Khi đó tàu chuyển động với vận tốc thực tế là:

$\overrightarrow {{v_*}} = \overrightarrow {{v_r}} + \overrightarrow {{v_n}} = \overrightarrow {A’C’}+\overrightarrow {C’B’}=\overrightarrow {A’B’}$

Xét tam giác A’B’C’ ta có:

$\widehat {A}$ = α (So le trong)

${\left| {\overrightarrow {{v_*}} } \right|^2} = {\left| {\overrightarrow {{v_r}} } \right|^2} + {\left| {\overrightarrow {{v_n}} } \right|^2} – 2\overrightarrow {{v_r}} .\overrightarrow {{v_n}} .\cos \alpha$

Giả sử tàu 2 xuất phát từ A ∈ d₁ và bánh lái luôn được giữ để tàu tạo với bờ một góc α. Gọi $\overrightarrow {{v_r}}$ và \overrightarrow {{v_n}} lần lượt là vận tốc riêng của tàu và vận tốc dòng nước. Gọi B, C là các điểm sao cho $\overrightarrow {{v_r}} = \overrightarrow {AC} ;\overrightarrow {{v_n}} = \overrightarrow {CB}$

Khi đó tàu chuyển động với vecto vận tốc thực tế là:

$\overrightarrow {{v_1}} = \overrightarrow {{v_r}} + \overrightarrow {{v_n}} = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB}$

Xét tam giác ABC có:

$\widehat {ABC} = {180^0} – \alpha$

$\begin{matrix}{\left|{\overrightarrow{{v_1}}}\right|^2}={\left|{\overrightarrow{{v_r}}}\right|^2}+{\left|{\overrightarrow{{v_n}}}\right|^2}-2\overrightarrow{{v_r}}.\overrightarrow{{v_n}}.\cos\left({{{180}^0}-\alpha}\right)\\\Rightarrow{\left|{\overrightarrow{{v_1}}}\right|^2}={\left|{\overrightarrow{{v_r}}}\right|^2}+{\left|{\overrightarrow{{v_n}}}\right|^2}+2\overrightarrow{{v_r}}.\overrightarrow{{v_n}}.\cos\alpha\\\end{matrix}$

Do 0⁰ < α < 90⁰ => cosα > 0

${\left| {\overrightarrow {{v_1}} } \right|^2} = {\left| {\overrightarrow {{v_r}} } \right|^2} + {\left| {\overrightarrow {{v_n}} } \right|^2} + 2\overrightarrow {{v_r}} .\overrightarrow {{v_n}} .\cos \alpha > {\left| {\overrightarrow {{v_1}} } \right|^2} = {\left| {\overrightarrow {{v_r}} } \right|^2} + {\left| {\overrightarrow {{v_n}} } \right|^2} – 2\overrightarrow {{v_r}} .\overrightarrow {{v_n}} .\cos \alpha$

${\left|{\overrightarrow{{v_1}}}\right|^2}={\left|{\overrightarrow{{v_r}}}\right|^2}+{\left|{\overrightarrow{{v_n}}}\right|^2}+2\overrightarrow{{v_r}}.\overrightarrow{{v_n}}.\cos\alpha>{\left|{\overrightarrow{{v_*}}}\right|^2}={\left|{\overrightarrow{{v_r}}}\right|^2}+{\left|{\overrightarrow{{v_n}}}\right|^2}-2\overrightarrow{{v_r}}.\overrightarrow{{v_n}}.\cos\alpha=>{\left|{\overrightarrow{{v_1}}}\right|^2}>{\left|{\overrightarrow{{v_*}}}\right|^2}$

Vì độ dài hai quãng đường AN và A’M’ của tàu 2 và tàu 1 chênh nhau không đáng kể nên ta coi nó bằng nhau. Do đó vì vận tốc tàu 2 lớn hơn tàu 1 nên tàu 2 là tàu đi qua bờ bên kia trước.