Toán lớp 10 tập 1 trang 71: Bài tập cuối chương 4
Toán lớp 10 tập 1 trang 71: Bài tập cuối chương 4
Giải toán lớp 10 tập 1 trang 71 bài tập cuối chương 4 có đáp án chi tiết cho từng bài tập trong sách giáo khoa toán lớp 10 tập 1 Kết nối tri thức. Mời các em học sinh cùng quý phụ huynh tham khảo.
Toán lớp 10 tập 1 trang 71
Bài 4.27 trang 71 Toán lớp 10 tập 1 Kết nối tri thức
Trong mặt phẳng tọa độ, cặp vectơ nào sau đây có cùng phương?
A. $\overrightarrow u = (2;3)$ và $\overrightarrow v = \left( {\frac{1}{2};6} \right)$
B. $\overrightarrow a = (\sqrt 2 ;6)$ và $\overrightarrow b = (1;3\sqrt 2 )$
C. $\overrightarrow i = (0;1)$ và $\overrightarrow j = (1;0)$
D. $\overrightarrow c = (1;3)$ và $\overrightarrow d = (2; – 6)$
Hướng dẫn::
A. Ta có: $\frac{2}{{\frac{1}{2}}} = 4 \ne \frac{3}{6}$ nên $\overrightarrow u$ và $\overrightarrow v$ không cùng phương.
B. Ta có: $\frac{{\sqrt 2 }}{1} = \frac{6}{{3\sqrt 2 }} = \sqrt 2 > 0$ nên $\overrightarrow a$
và $\overrightarrow b$ cùng phương, hơn nữa là cùng hướng
Chọn đáp án B. $\overrightarrow v = \left( {4;6} \right)$
C. Ta có: $\overrightarrow i .\overrightarrow j = 0.1 + 1.0 = 0 \Rightarrow \overrightarrow i \bot \overrightarrow j$
Vậy $\overrightarrow i$ và $\overrightarrow j$ không cùng phương.
D. Ta có: $\frac{1}{2} \ne \frac{3}{{ – 6}}$ nên $\overrightarrow c$ và $\overrightarrow d$ không cùng phương
Bài 4.28 trang 71 Toán lớp 10 tập 1 Kết nối tri thức
Trong mặt phẳng tọa độ, cặp vectơ nào sau đây vuông góc với nhau?
A. $\overrightarrow u$ = (2;3) và $\overrightarrow v = \left( {4;6} \right)$
B. $\overrightarrow a$ = (1; – 1) và $\overrightarrow b$ = ( – 1;1)
C. $\overrightarrow z = (a;b)$ và $\overrightarrow t = ( – b;a)$
D. $\overrightarrow n = (1;1)$ và $\overrightarrow k = (2;0)$
Hướng dẫn::
Chọn đáp án C
D. Ta có: $\overrightarrow n .\overrightarrow k = 1.2 + 1.0 = 2 \ne 0$ nên $\overrightarrow n$ và $\overrightarrow k$ không vuông góc với nhau
Bài 4.29 trang 71 Toán lớp 10 tập 1 Kết nối tri thức
Trong mặt phẳng tọa độ, vectơ nào sau đây có độ dài bằng 1?
A. $\overrightarrow a$ = (1;1)
B. $\overrightarrow b$ = (1; – 1)
C. $\overrightarrow c = \left( {2;\frac{1}{2}} \right)$
D. $\overrightarrow d = \left( {\dfrac{1}{{\sqrt 2 }};\dfrac{{ – 1}}{{\sqrt 2 }}} \right)$
Hướng dẫn::
Chọn D
Bài 4.30 trang 71 Toán lớp 10 tập 1 Kết nối tri thức
Góc giữa vectơ $\overrightarrow a$ = $\left( {1; – 1} \right)$ và vectơ $\overrightarrow b$ = ( – 2;0) có số đo bằng:
A. ${90^o}$
B. ${0^o}$
C. ${135^o}$
D. ${45^o}$
Hướng dẫn::
Ta có $\overrightarrow a .\overrightarrow b = 1.( – 2) + ( – 1).0 = – 2 \ne 0.$
Lại có $|\overrightarrow a | = \sqrt {{1^2} + {{( – 1)}^2}} = \sqrt 2 ;\;|\overrightarrow b | = \sqrt {{{( – 2)}^2} + {0^2}} = 2.$
$\Rightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.\;|\overrightarrow b |}} = \frac{{ – 2}}{{\sqrt 2 .2}} = \frac{{ – \sqrt 2 }}{2}$
$\Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {135^o}$
Chọn C
Bài 4.31 trang 71 Toán lớp 10 tập 1 Kết nối tri thức
Khẳng định nào sau đây là đúng?
A. $( {\overrightarrow a .\overrightarrow b } )\overrightarrow c = \overrightarrow a \,\,( {\overrightarrow b .\overrightarrow c })$
B. ${( {\overrightarrow a .\overrightarrow b })^2} = {\overrightarrow a ^2}\,.\,{\overrightarrow b ^2}$
C. $\overrightarrow a .\overrightarrow b = | {\overrightarrow a } |.\left| {\overrightarrow b } \right|\,\sin ( {\overrightarrow a ,\overrightarrow b } )$
D. $\overrightarrow a \,\,( {\overrightarrow b – \overrightarrow c }) = \overrightarrow a .\overrightarrow b – \overrightarrow a .\,\overrightarrow c$
Hướng dẫn::
Chọn D. Đây là một tính chất của tích vô hướng.
A. Sai vì
$({\overrightarrow a .\overrightarrow b})\overrightarrow c = [ {|\overrightarrow a |.|\overrightarrow b |\;\,\cos ( {\overrightarrow a ,\overrightarrow b } )} ].\overrightarrow c \ne \overrightarrow a \,\,( {\overrightarrow b .\overrightarrow c }) = \overrightarrow a \,\,[ {|\overrightarrow b |.|\overrightarrow c |\;\,\cos ( {\overrightarrow b ,\overrightarrow c })}]$
B. Sai vì
$(\overrightarrow a .\overrightarrow b)^2 = {[{\overrightarrow a .\overrightarrow b = | {\overrightarrow a } |.| {\overrightarrow b }|\,\cos ( {\overrightarrow a ,\overrightarrow b })}]^2} = {\overrightarrow a ^2}\,.\,{\overrightarrow b ^2}.{\cos ^2}( {\overrightarrow a ,\overrightarrow b } ) \ne \;\;{\overrightarrow a ^2}\,.\,{\overrightarrow b ^2}$
C. Sai vì
$(\overrightarrow a .\overrightarrow b)^2 = {[{\overrightarrow a .\overrightarrow b = | {\overrightarrow a } |.| {\overrightarrow b }|\,\cos ( {\overrightarrow a ,\overrightarrow b })}]^2} = {\overrightarrow a ^2}\,.\,{\overrightarrow b ^2}.{\cos ^2}( {\overrightarrow a ,\overrightarrow b } ) \ne \;\;{\overrightarrow a ^2}\,.\,{\overrightarrow b ^2}$
Bài 4.32 trang 71 Toán lớp 10 tập 1 Kết nối tri thức
Cho hình vuông ABCD có cạnh a. Khẳng định nào sau đây là đúng?
A. $\left( {\overrightarrow {AB} ,\overrightarrow {BD} } \right) = {45^o}$
B. $\left( {\overrightarrow {AC} ,\overrightarrow {BC} } \right) = {45^o}$ và $\overrightarrow {AC} .\overrightarrow {BC} = {a^2}$
C. $\overrightarrow {AC} .\overrightarrow {BD} = {a^2}\sqrt 2$
D. $\overrightarrow {BA} .\overrightarrow {BD} = – {a^2}$
Hướng dẫn::
Chọn B
Bài 4.33 trang 71 Toán lớp 10 tập 1 Kết nối tri thức
Trên cạnh BC của tam giác ABC lấy điểm M sao cho MB = 3 MC.
a) Tìm mối liên hệ giữa hai vectơ $\overrightarrow {MB}$ và $\overrightarrow {MC}$ ngược hướng với nhau.
Lại có: MB = 3 MC $\Rightarrow \overrightarrow {MB} = – 3.\overrightarrow {MC}$
b) Ta có: $\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM}$
mà BM = $\dfrac{3}{4}BC nên \overrightarrow {BM} = \dfrac{3}{4}\overrightarrow {BC}$
$\Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \dfrac{3}{4}\overrightarrow {BC}$
Lại có $\overrightarrow {BC} = \overrightarrow {AC} – \overrightarrow {AB}$ quy tắc hiệu
$\Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \dfrac{3}{4}\left( {\overrightarrow {AC} – \overrightarrow {AB} } \right) = \dfrac{1}{4}.\overrightarrow {AB} + \dfrac{3}{4}.\overrightarrow {AC}$
Vậy $\overrightarrow {AM} = \dfrac{1}{4}.\overrightarrow {AB} + \dfrac{3}{4}.\overrightarrow {AC}$
Toán lớp 10 tập 1 trang 72
Bài 4.34 trang 72 Toán lớp 10 tập 1 Kết nối tri thức
Cho hình bình hành ABCD. Chứng minh rằng với mọi điểm M, ta có:
$\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} .$
Hướng dẫn::
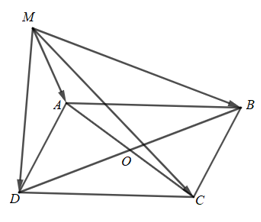
Gọi O là giao điểm của AC và BD
Suy ra O là trung điểm của AC và BD
$\Rightarrow \overrightarrow{OA} + \overrightarrow{OC} = \overrightarrow{0} \quad \text{và} \quad \overrightarrow{OB} + \overrightarrow{OD} = \overrightarrow{0}.$
Ta có:
1.
$\overrightarrow{MA} + \overrightarrow{MC} = \overrightarrow{MO} + \overrightarrow{OA} + \overrightarrow{MO} + \overrightarrow{OC} = 2\overrightarrow{MO} + (\overrightarrow{OA} + \overrightarrow{OC}) = 2\overrightarrow{MO}.$
(Vì $( \overrightarrow{OA} + \overrightarrow{OC} = \overrightarrow{0} ).$
2. $\overrightarrow{MB} + \overrightarrow{MD} = \overrightarrow{MO} + \overrightarrow{OB} + \overrightarrow{MO} + \overrightarrow{OD} = 2\overrightarrow{MO} + (\overrightarrow{OB} + \overrightarrow{OD}) = 2\overrightarrow{MO}.$
(Vì $( \overrightarrow{OB} + \overrightarrow{OD} = \overrightarrow{0} )).$
Suy ra:
$\overrightarrow{MA} + \overrightarrow{MC} = \overrightarrow{MB} + \overrightarrow{MD}.$
Vậy:
$\overrightarrow{MA} + \overrightarrow{MC} = \overrightarrow{MB} + \overrightarrow{MD}.$
Bài 4.35 trang 72 Toán lớp 10 tập 1 Kết nối tri thức
Trong mặt phẳng tọa độ Oxy, cho A (2; 1), B (-2; 5) và C (-5; 2).
a) Tìm tọa độ của các vectơ \overrightarrow {BA} và \overrightarrow {BC}
b) Chứng minh rằng A, B, C là ba đỉnh của một tam giác vuông. Tính diện tích và chu vi của tam giác đó.
c) Tìm tọa độ trọng tâm G của tam giác ABC.
d) Tìm tọa độ của điểm D sao cho tứ giác BCAD là một hình bình hành.
Hướng dẫn::
a) Ta có: $\overrightarrow {BA}$ = (2 – ( – 2);1 – 5) = (4; – 4)
$\overrightarrow {BC}$ = ( – 5 – ( – 2);2 – 5) = ( – 3; – 3)
b) Ta có: $\overrightarrow {BA} .\overrightarrow {BC}$ = 4.( – 3) + ( – 4).( – 3) = 0
$\Rightarrow \overrightarrow {BA} \bot \overrightarrow {BC} hay \widehat {ABC} = {90^o}$
Vậy tam giác ABC vuông tại B.
Lại có: AB = $\left| {\overrightarrow {BA} } \right| = \sqrt {{4^2} + {{( – 4)}^2}} = 4\sqrt 2 ; BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{3^2} + {{( – 3)}^2}} = 3\sqrt 2$
Và AC = $\sqrt {A{B^2} + B{C^2}} = 5\sqrt 2$ (do $\Delta$ ABC vuông tại B)
Diện tích tam giác ABC là: ${S_{ABC}} = \frac{1}{2}.AB.BC = \frac{1}{2}.4\sqrt 2 .3\sqrt 2$ = 12
Chu vi tam giác ABC là: AB + BC + AC = $4\sqrt 2 + 3\sqrt 2 + 5\sqrt 2 = 12\sqrt 2$
c) Tọa độ của trọng tâm G là $\left( {\frac{{2 + ( – 2) + ( – 5)}}{3};\frac{{1 + 5 + 2}}{3}} \right) = \left( {\frac{{ – 5}}{3};\frac{8}{3}} \right)$
d) Giả sử điểm D thỏa mãn BCAD là một hình bình hành có tọa độ là (a; b).
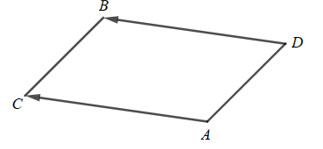
Ta có: $\overrightarrow {BC}$ = ( – 3; – 3) và $\overrightarrow {AD} = (a – 2;b – 1)$
Vì BCAD là một hình bình hành nên $\overrightarrow {AD} = \overrightarrow {BC}$
$\begin{array}{l} \Leftrightarrow (a – 2;b – 1) = ( – 3; – 3)\\ \Leftrightarrow \left\{ \begin{array}{l}a – 2 = – 3\\b – 1 = – 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = – 1\\b = – 2\end{array} \right.\end{array}$
Vậy D có tọa độ (-1; -2)
Bài 4.36 trang 72 Toán lớp 10 tập 1 Kết nối tri thức
Trong mặt phẳng tọa độ Oxy, cho A (1; 2), B (3; 4), C (-1; -2) và D (6;5).
a) Hãy tìm tọa độ của các vectơ $\overrightarrow {AB}$ và $\overrightarrow {CD}$
b) Hãy giải thích tại sao các vectơ $\overrightarrow {AB}$ và $\overrightarrow {CD}$ cùng phương.
c) Giả sử E là điểm có tọa độ (a; 1). Tìm a để các vectơ $\overrightarrow {AC}$ và $\overrightarrow {BE}$ cùng phương
d) Với a tìm được, hãy biểu thị vectơ $\overrightarrow {AE}$
theo các vectơ $\overrightarrow {AB}$ và $\overrightarrow {AC} .$
Hướng dẫn::
a) Ta có: $\overrightarrow {AB} = (3 – 1;4 – 2) = (2;2)$ và $\overrightarrow {CD} = (6 – ( – 1);5 – ( – 2)) = (7;7)$
b) Dễ thấy: $\frac{2}{7}$=$\frac{2}{7}$
Vậy hai vectơ \overrightarrow {AB} và \overrightarrow {CD} cùng phương.
c) Ta có: $\overrightarrow {AC} = ( – 1 – 1; – 2 – 2) = ( – 2; – 4)$ và $\overrightarrow {BE} = (a – 3;1 – 4) = (a – 3; – 3)$
Để $\overrightarrow {AC} và \overrightarrow {BE}$ cùng phương thì $\frac{{a – 3}}{{ – 2}} = \frac{{ – 3}}{{ – 4}} \Leftrightarrow a – 3 = – \frac{3}{2} \Leftrightarrow a = \frac{3}{2}$
Vậy a = $\frac{3}{2}$ hay $E\left( {\frac{3}{2};1} \right)$ thì hai vecto a = $\frac{3}{2}$ hay $E\left( {\frac{3}{2};1} \right)$ và $\overrightarrow {BE}$ cùng phương
d)
Ta có: $\overrightarrow {BE} = \left( {\frac{3}{2} – 3; – 3} \right) = \left( { – \frac{3}{2}; – 3} \right) ; \overrightarrow {AC} = ( – 2; – 4)$
$\Rightarrow \overrightarrow {BE} = \frac{3}{4}.\overrightarrow {AC} mà \overrightarrow {AE} = \overrightarrow {AB} + \overrightarrow {BE}$ quy tắc cộng
$\Rightarrow \overrightarrow {AE} = \overrightarrow {AB} + \frac{3}{4}.\overrightarrow {AC}$
Bài 4.37 trang 72 Toán lớp 10 tập 1 Kết nối tri thức
Cho vectơ $\vec{a} \neq \vec{0}$. Chứng minh rằng $\frac{1}{||\vec{a}||}\vec{a}$ (hay còn được viết là $\frac{\vec{a}}{||\vec{a}||}$) là một vectơ đơn vị, cùng hướng với vectơ $\vec{a}$.
Hướng dẫn:
Ta thấy $\frac{1}{||\vec{a}||}>0$ ($\vec{a} \neq \vec{0}$) nên $\frac{1}{||\vec{a}||}\vec{a}$ là vectơ cùng hướng với vectơ $\vec{a}$.
Độ dài của vectơ $\frac{1}{||\vec{a}||}\vec{a}$ là: $||\frac{1}{||\vec{a}||}\vec{a}|| = |\frac{1}{||\vec{a}||}| ||\vec{a}|| = \frac{1}{||\vec{a}||}.||\vec{a}|| = 1$
Vậy vectơ $\frac{1}{||\vec{a}||}\vec{a}$ (hay còn được viết là $\frac{\vec{a}}{||\vec{a}||}$) là một vectơ đơn vị, cùng hướng với vectơ $\vec{a}$.
Bài 4.38 trang 72 Toán lớp 10 tập 1 Kết nối tri thức
Cho ba vectơ $\vec{a}$, $\vec{b}$, $\vec{u}$ với $||\vec{a}|| = ||\vec{b}|| = 1$ và $\vec{a} \perp \vec{b}$. Xét một hệ trục Oxy với các vectơ đơn vị $\vec{i} = \vec{a}$, $\vec{j} = \vec{b}$. Chứng minh rằng:
a) Vectơ $\vec{u}$ có tọa độ là $(\vec{u}.\vec{a}; \vec{u}.\vec{b})$.
b) $\vec{u} = (\vec{u}.\vec{a})\vec{a} + (\vec{u}.\vec{b})\vec{b}$.
Hướng dẫn:
a) Vì $\vec{i} = \vec{a}$ và $\vec{j} = \vec{b}$ là các vectơ đơn vị của hệ trục Oxy, ta có $\vec{u} = x\vec{i} + y\vec{j} = x\vec{a} + y\vec{b}$.
Lấy tích vô hướng của $\vec{u}$ với $\vec{a}$: $\vec{u}.\vec{a} = (x\vec{a} + y\vec{b}).\vec{a} = x(\vec{a}.\vec{a}) + y(\vec{b}.\vec{a}) = x||\vec{a}||^2 + y(0) = x$ (vì $\vec{a} \perp \vec{b}$ và $||\vec{a}||=1$).
Tương tự, lấy tích vô hướng của $\vec{u}$ với $\vec{b}$: $\vec{u}.\vec{b} = (x\vec{a} + y\vec{b}).\vec{b} = x(\vec{a}.\vec{b}) + y(\vec{b}.\vec{b}) = x(0) + y||\vec{b}||^2 = y$.
Vậy tọa độ của $\vec{u}$ là $(\vec{u}.\vec{a}; \vec{u}.\vec{b})$.
b) Từ a), ta có $\vec{u} = x\vec{a} + y\vec{b} = (\vec{u}.\vec{a})\vec{a} + (\vec{u}.\vec{b})\vec{b}$.
Bài 4.39 trang 72 Toán lớp 10 tập 1 Kết nối tri thức
Trên sông, một ca nô chuyển động thẳng đều theo hướng S15°E (xem chú thích ở Bài 3.8, trang 42) với vận tốc có độ lớn bằng 20km/h. Tính vận tốc riêng của ca nô, biết rằng nước trên sông chảy về hướng đông với vận tốc có độ lớn bằng 3 km/h.
Hướng dẫn:
Trên sông, một ca nô chuyển động thẳng đều theo hướng S15°E (ảnh 1)
Ta mô tả bài toán bằng hình vẽ trên, trong đó:
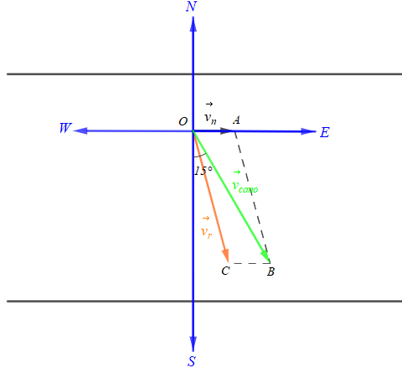
\item $\overrightarrow{OE}$ là hướng đông, $\overrightarrow{OS}$ là hướng nam, $\overrightarrow{OW}$ là hướng tây, $\overrightarrow{ON}$ là hướng bắc;
$\overrightarrow{OA}$ biểu diễn vectơ vận tốc của dòng nước $\vec{v}_n$ và $OA = ||\vec{v}_n|| = 3$;
$\overrightarrow{OB}$ là hướng S15°E biểu diễn vectơ vận tốc chuyển động của ca nô $\vec{v}_{cano}$ tạo với $\overrightarrow{OS}$ một góc 15° và $OB = ||\vec{v}_{cano}|| = 20$;
\end{itemize}
Lấy điểm C sao cho OABC là hình bình hành. Khi đó $\overrightarrow{OC}$ biểu diễn vectơ vận tốc riêng $\vec{v}_r$ của ca nô.
Vì $\overrightarrow{OB}$ tạo với $\overrightarrow{OS}$ một góc 15° nên $\overrightarrow{OB}$ tạo với $\overrightarrow{OA}$ một góc là 90° − 15° = 75°, tức là $\angle AOB = 75^\circ$.
Xét tam giác OAB có: $AB^2 = OA^2 + OB^2 – 2.OA.OB.\cos\angle AOB$
$\Rightarrow AB^2 = 3^2 + 20^2 – 2.3.20.\cos 75^\circ$
$\Rightarrow AB \approx 19.44$
Vì OABC là hình bình hành nên $OC = AB \approx 19.44$ (tính chất hình bình hành)
Suy ra $||\vec{v}_r|| = ||\overrightarrow{OC}|| = OC \approx 19.44$ (km/h)
Vậy vận tốc riêng của ca nô khoảng 19.44 km/h.
