Toán lớp 10 tập 1 trang 73 Bài 12: Số gần đúng và sai số

Giải  toán lớp 10 tập 1 trang 73 bài 12 có đáp án chi tiết cho từng bài tập trong sách giáo khoa toán lớp 10 tập 1 Kết nối tri thức. Mời các em học sinh cùng quý phụ huynh tham khảo.

Toán lớp 10 tập 1 trang 73

Mở đầu trang 73 Toán lớp 10 tập 1 Kết nối tri thức

Đỉnh Everest được mệnh danh là “nóc nhà của thế giới”, bởi đây là đỉnh núi cao nhất trên Trái Đất so với mực nước biển. Có rất nhiều con số khác nhau đã từng được công bố về chiều cao của đỉnh Everest:

8 848 m; 8 848,13m; 8 844,43m; 8 850m; …

Vì sao lại có nhiều kết quả khác nhau như vậy và đâu là con số chính xác? Chúng ta sẽ cùng tìm câu trả lời trong bài học này, sau khi tìm hiểu về số gần đúng và sai số.

Hướng dẫn::

Khi đo độ cao đỉnh núi Everest người ta không thể đo trực tiếp một cách chính xác mà phải thông qua tính toán.

Mỗi vị trí quan sát hoặc trong tính toán, có những con số không thể lấy chính xác đo đó kết quả thu được cũng không giống nhau.

Ngoài ra có thể người ta đã làm tròn kết quả để được một con số gọn mà chính xác nhất có thể, nên các kết quả cũng khác nhau.

Qua nhiều lần đo, người ta đưa ra được chiều cao của đỉnh Everest là 8 848,86 m.

1. Số gần đúng

Toán lớp 10 tập 1 trang 74

HOạT ĐộNG 1 trang 74 Toán lớp 10 tập 1 Kết nối tri thức

Ngày 8–12–2020, Trung Quốc và Nepal ra thông cáo chung khẳng định chiều cao mới đo được của đỉnh núi cao nhất thế giới Everest là 8 848,86m.

Trong các số được đưa ra ở tình huống mở đầu, số nào gần với số được công bố ở trên?

Hướng dẫn::

Ta có:

|8 848,86 – 8 848| = 0,86;

|8 848,86 – 8 848,13| = 0,73;

|8 848,86 – 8 844,43| = 4,43;

|8 848,86 – 8 850| = 1,14.

Trong các số 0,86; 0,73; 4,43; 1,14 thì số 0,73 là số nhỏ nhất.

Do đó trong các số 8 848 m; 8 848,13 m; 8 844,43 m; 8 850 m thì số 8 848,13 m là số gần nhất với số được công bố ngày 8–12–2020.

HOạT ĐộNG 2 trang 74 Toán lớp 10 tập 1 Kết nối tri thức

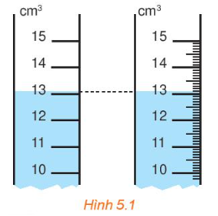
Trang và Hòa thực hiện đo thể tích một cốc nước bằng hai ống đong có vạch chia được kết quả như Hình 5.1. Hãy cho biết số đo thể tích trên mỗi ống.

Trang và Hòa thực hiện đo thể tích một cốc nước bằng hai ống đong (ảnh 1)

Hướng dẫn:

Giả sử ống đong nước thứ nhất là Trang đo và ống đong nước thứ hai là Hòa đo.

Trang và Hòa thực hiện đo thể tích một cốc nước bằng hai ống đong (ảnh 1)

Khi đó ống thứ nhất đo được là 13 cm3, ống thứ hai là 13,1 cm3.

Câu hỏi trang 74 Toán lớp 10 tập 1 Kết nối tri thức Hãy lấy một ví dụ khác về số gần đúng.

Hướng dẫn::

Ta có: $\sqrt{5} \approx 2,236.$

Do đó, số gần đúng của $\sqrt{5} \$ là 2,236$

Toán lớp 10 tập 1 trang 77

Bài 5.1 trang 77 Toán lớp 10 tập 1 Kết nối tri thức

Trong các số sau, những số nào là số gần đúng?

a) Cân một túi gạo cho kết quả là 10,2kg

b) Bán kính Trái Đất là 6 371 km.

c) Trái Đất quay một vòng quanh Mặt Trời mất 365 ngày.

Hướng dẫn::

a) Khi cân một túi gạo thì ta kết quả là một số gần đúng vì đây là một cách đo đạc.

b) Ta không biết chính xác bán kính Trái Đất nên 6 371 cũng là số gần đúng.

c) Trái Đất quay một vòng quanh Mặt Trời mất 365 ngày cũng là số gần đúng.

Bài 5.2 trang 77 Toán lớp 10 tập 1 Kết nối tri thức

Giải thích kết quả “Đo độ cao của một ngọn núi cho kết quả là 1 235 +5 m” và thực hiện làm tròn số gần đúng.

Hướng dẫn::

– Giải thích: “Đo độ cao của một ngọn núi cho kết quả là 1 235 ± 5m

Độ cao của ngọn núi gần với 1235m và độ chính xác là 5m

Bài 5.3 trang 77 Toán lớp 10 tập 1 Kết nối tri thức

Sử dụng máy tính cầm tay tìm số gần đúng cho $\sqrt[3]{7}$ với độ chính xác 0,0005.

Hướng dẫn::

Ta chọn số gần đúng là 1,912931183.

Độ chính xác d=0,0005 nên ta có hàng làm tròn là hàng phần nghìn.

Số ở hàng phần nghìn là số 2, số bên phải là số 9>5 nên ta tăng 2 thêm 1 đơn vị và được số quy tròn của 1,912931183 là 1,913

Bài 5.4 trang 77 Toán lớp 10 tập 1 Kết nối tri thức

Các nhà vật lí sử dụng ba phương pháp đo hằng số Hubble lần lượt cho kết quả như sau:

$67,31 \pm 0,96;$

$67,90 \pm 0,55;$

$67,74 \pm 0,46.$

Phương pháp nào chính xác nhất tính theo sai số tương đối?

Hướng dẫn::

Phương pháp 1: $67,31 \pm 0,96$

a = 67,31;d = 0,96

Sai số tương đối ${\delta _1} \le \frac{d}{{\left| a \right|}} = \frac{{0,96}}{{67,31}} \approx 0,014$

Phương pháp 2: $67,90 \pm 0,55$

a = 67,90;d = 0,55

Sai số tương đối ${\delta _2} \le \frac{d}{{\left| a \right|}} = \frac{{0,55}}{{67,90}} \approx 8,{1.10^{ – 3}}$ = 0,0081

Phương pháp 1: $67,74 \pm 0,46$ a = 67,74;d = 0,46

Sai số tương đối ${\delta _3} \le \frac{d}{{\left| a \right|}} = \frac{{0,46}}{{67,74}} \approx 6,{8.10^{ – 3}} = 0,0068$

Ta thấy 0,14 > 0,0081 > 0,0068

=> phương pháp 3 có chính xác nhất.

Bài 5.5 trang 77 Toán lớp 10 tập 1 Kết nối tri thức

An và Bình cùng tính chu vi của hình tròn bán kính 2 cm với hai kết quả như sau:

Kết quả của An: ${S_1} = 2\pi R \approx 2.3,14.2$ = 12,56cm;

Kết quả của Bình: ${S_2} = 2\pi R \approx 2.3,1.2$ = 12,4cm.

Hỏi:

a) Hai giá trị tính được có phải là các số gần đúng không?

b) Giá trị nào chính xác hơn?

Hướng dẫn::

a) Vì công thức chu vi đường tròn là $2\pi R$ với R là độ dài bán kính, trong đó $\pi$

là số không thể tính chính xác được mà chỉ có thể lấy số gần đúng nên hai giá trị tính được là số gần đúng.

b)

Kết quả của An: ${S_1} = 2\pi R \approx 2.3,14.2$ = 12,56 cm:

Kết quả của Bình: ${S_2} = 2\pi R \approx$ 2.3,1.2 = 12,4cm.

Ta thấy 3,14 < 3,1 = > ${S_1} < {S_2}$

= > $\left| {2\pi R – {S_1}} \right| > \left| {2\pi R – {S_2}} \right|$

=> Kết quả của An chính xác hơn.

Bài 5.6 trang 77 Toán lớp 10 tập 1 Kết nối tri thức

Làm tròn số 8 316,4 đến hàng chục và 9,754 đến hàng phần trăm rồi tính sai số tuyệt đối của số quy tròn.

Hướng dẫn::

– Làm tròn số 8 316,4 đến hàng chục

Số làm tròn là số 1, số bên phải số 1 là số 6>5

=> Tăng thêm 1 đơn vị

=> Số quy tròn là: 8 320

Sai số tuyệt đối: $\left| {8320 – 8316,4} \right| = 3,6$

– Làm tròn số 9,754 đến hàng phần trăm

Số làm tròn là số 5, số bên phải số 5 là số 4<5

=> Giữ nguyên 5 và bỏ các số bên phải đi.

=> Số quy tròn là: 9,75

Sai số tuyệt đối: $\left| {9,754 – 9,75} \right| = 0,004$