Bài 22: Ba đường conic

Giải  toán lớp 10 tập 2 trang 56 bài 22 có đáp án chi tiết cho từng bài tập trong sách giáo khoa toán lớp 10 tập 2 Kết nối tri thức. Mời các em học sinh cùng quý phụ huynh tham khảo.

Toán lớp 10 tập 2 trang 56

Bài 7.19 trang 56 Toán 10 tập 2 Kết nối tri thức

Cho elip có phương trình: $\frac{x^{2}}{36}+\frac{y^{2}}{9}=1$. Tìm tiêu điểm và tiêu cự của elip.

Hướng dẫn:

Ta có: a²= 36, b² = 9, c = $\sqrt{a^{2}-b^{2}}=\sqrt{27}.$

Tiêu điểm F₁$(-\sqrt{27};0)$ và F₂$(\sqrt{27};0).$ ,tiêu cự 2c = $2\sqrt{27}.$

Bài 7.20 trang 56 Toán lớp 10 tập 2 Kết nối tri thức

Cho hypebol có phương trình: $\frac{x^{2}}{7}-\frac{y^{2}}{9}=1$

. Tìm tiêu điểm và tiêu cự của hypebol.

Hướng dẫn:

Từ phương trình: $\frac{x^{2}}{7}-\frac{y^{2}}{9}=1$

Ta có: a² = 7, b² = 9, c = $\sqrt{a^{2}+b^{2}}=4.$

Tiêu điểm F1(-4;0) và F2(4;0).

Tiêu cự 2c = 8

Bài 7.21 trang 56 Toán lớp 10 tập 2 Kết nối tri thức

Cho parabol có phương trình: y2 = 8x. Tìm tiêu điểm và đường chuẩn của parabol.

Hướng dẫn:

Ta có: 2p = 8 nên p = 4.

Tiêu điểm F(2; 0) và đường chuẩn $\Delta$ : x = -2.

Bài 7.22 trang 56 Toán lớp 10 tập 2 Kết nối tri thức

Lập phương trình chính tắc của elip đi qua điểm A(5; 0) và có một tiêu điểm là F2(3; 0).

Hướng dẫn:

Elip (E) có dạng: $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$

với a>b>0.

(E) đi qua A(5; 0) nên $\frac{5^{2}}{a^{2}}+\frac{0^{2}}{b^{2}}=1$

$\Rightarrow$ a = 5.

(E) có tiêu điểm F2(3; 0) nên c = 3

$\Rightarrow b = \sqrt{a^{2}-c^{2}}=4$

Vậy phương trình chính tắc của (E):$\frac{x^{2}}{25}+\frac{y^{2}}{16}=1$

Bài 7.23 trang 56 Toán lớp 10 tập 2 Kết nối tri thức

Lập phương trình chính tắc của parabol đi qua điểm M(2; 4).

Hướng dẫn:

Phương trình parabol (P) có dạng: y² = 2px.

(P) đi qua M(2; 4) nên 4² = 2p.2

$\Rightarrow$ 2p =8

Vậy phương trình (P): y² = 8x.

Bài 7.24 trang 56 Toán lớp 10 tập 2 Kết nối tri thức

Có hai trạm phát tín hiệu vô tuyến đặt tại hai vị trí A, B cách nhau 300 km. Tại cùng một thời điểm, hai trạm cùng phát tín hiệu với vận tốc 292 000 km/s để một tàu thủy thu và đo độ lệch thời gian. Tín hiệu từ A đến sớm hơn tín hiệu từ B là 0,0005 s. Từ thông tin trên, ta có thể xác định được tàu thủy thuộc đường hybebol nào? Viết phương trình chính tắc của hypebol đó theo đơn vị kilômét.

Hướng dẫn:

Chọn hệ trục tọa độ Oxy sao cho A, B nằm trên trục Ox, tia Ox trùng với tia OB, O là trung điểm của AB. Nên tọa độ hai điểm là: A (-150; 0) và B (150; 0)

Khi đó vị trí tàu thủy là điểm M nằm trên hypebol có 2 tiêu điểm là A và B.

Tín hiệu từ A đến sớm hơn tín hiệu từ B là 0,0005 s nên ta có: |MA – MB| = 0,0005.292 000 = 146 km.

Gọi phương trình chính tắc của hypebol có dạng: $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$

với a, b > 0.

Do |MA – MB| = 146 = 2a $\Leftrightarrow a$ = 73.

Do hai tiêu điểm là: A(-150; 0) và B(150; 0) nên c = 150

$\Rightarrow b = \sqrt{c^{2}-a^{2}}=\sqrt{17171}$

Vậy phương trình chính tắc của hypebol cần tìm là: $\frac{x^{2}}{5329}$

Bài 7.25 trang 56 Toán 10 tập 2 Kết nối tri thức

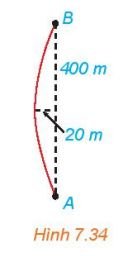
Khúc cua của một con đường có dạng hình parabol, điểm đầu vào khúc cua là A, điểm cuối là B, khoảng cách AB = 400m. Đỉnh parabol (P) của khúc của cách đường thẳng AB một khoảng 20 m và cách đều A, B.

a. Lập phương trình chính tắc của (P), với 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 m trên thực tế.

b. Lập phương trình chính tắc của (P), với 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 km trên thực tế.

Hướng dẫn:

Chọn hệ trục tọa độ sao cho đỉnh của parabol trùng với gốc tọa độ O(0; 0) (như hình vẽ).

a. Nếu 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 m trên thực tế thì tọa độ các điềm là: A(20; -200) và B(20; 200) thuộc vào parabol có dạng y² = 2px

Thay tọa độ điểm A và ta có: 2002 = 2p.20 $\Rightarrow$ 2p = 2000

Vậy parabol có dạng: y² = 2000.x

b. Nếu 1 đơn vị đo trong mặt phẳng tọa độ tương ứng 1 km trên thực tế thì tọa độ các điềm là: A(0,02; -0,2) và B(0,02; 0,2) thuộc vào parabol có dạng y² = 2px

Thay tọa độ điểm A và ta có:0,22 = 2p.0,02 $\Rightarrow$ 2p = 2

Vậy parabol có dạng: y² = 2.x